Logic and AI

1. Give an example of a materially valid deductive inference (which has not occurred anywhere in the course yet). Show how it can be transformed into a logically valid inference by adding a premise. (1 point)

2. Give an example of an inductively strong inference (again, not from anywhere in the course). Show that it is deductively invalid by describing a reasoning scenario, where its premises are true but the conclusion isn’t. Then provide a (non-formal) argument that the premise nevertheless makes the conclusion (more) likely. (1 point)

3. For each of your examples, explain in one to two paragraphs why understanding this kind of inference is important to AI research and development. (2 points)

Reverse Polish notation

In the exercises for the chapter on formal languages, you encountered Polish notation , which gets achieves unique readability without parentheses.

For this question, we’ll consider a variant of Polish notation known as reverse Polish notation , which rather than writing logical operations before their operands in so-called “prefix notation” of the Polish system, reverse Polish notation writes the operators after in so-called “postfix notation.”

For simplicity, we’ll use the ordinary symbols , , , , 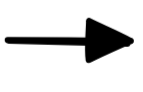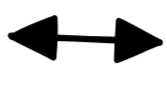rather than the Polish N, K, A, C, B for the logical operators.

Our alphabet, thus is:

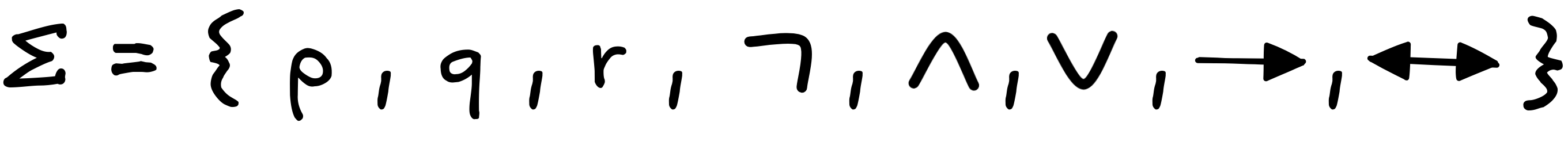
Note the absence of parentheses.

1. Determine the grammar of reverse Polish notation in BNF. (1 point)

2. Determine the corresponding re-write rules and generate the parsing tree for the formula 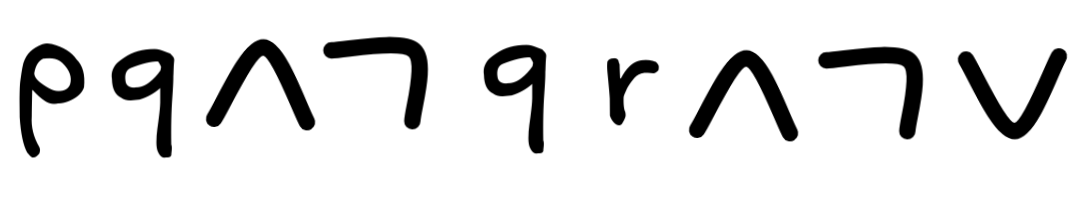. (2 points)

3. Give an argument why 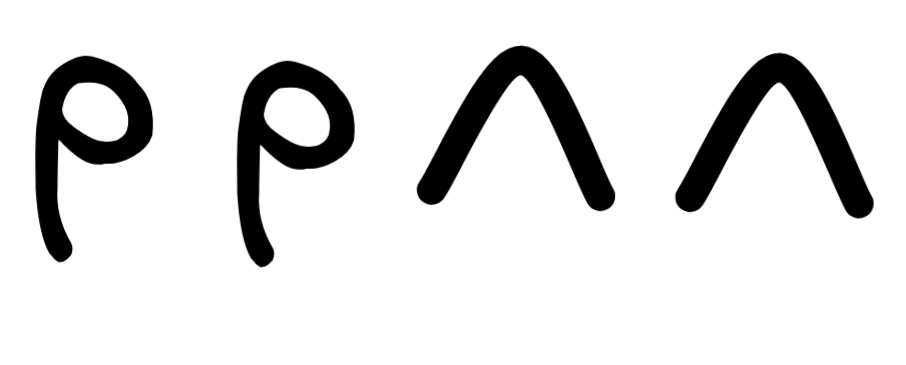isn’t a formula in reverse Polish notation. (1 point)

4. A very important parsing algorithm is the so-called shunting yard algorithm . This algorithm can be used to transform formulas from ordinary infix notation into reverse Polish notation. Here’s a quick description of the algorithm:

   • We keep two separate areas, the output queue and the stack:

     • The queue constructs our re-written formula, step-by-step.
     • The stack is processed first-to-last (“last in, first out” or LIFO). Writing an expression at the beginning of the stack is called “pushing onto” the stack. Removing an expression from the start of the stack is “pop” it off the stack.

   • We go through the symbols of our formula from left to right and apply the following rules to transform the expression:

     1. For a propositional variable, we write it directly to the output queue.
     2. For a left parenthesis ( , we push it onto the stack.
     3. For a right parenthesis ) , we pop operators from the stack to the queue until we either encounter a left parenthesis or the stack is empty. We discard the parenthesis pair.
     4. For a logical operator, we push it onto the stack.
     5. At the end, we pop any remaining operators to the output queue.

   Apply this algorithm step-by-step to transform the infix formula 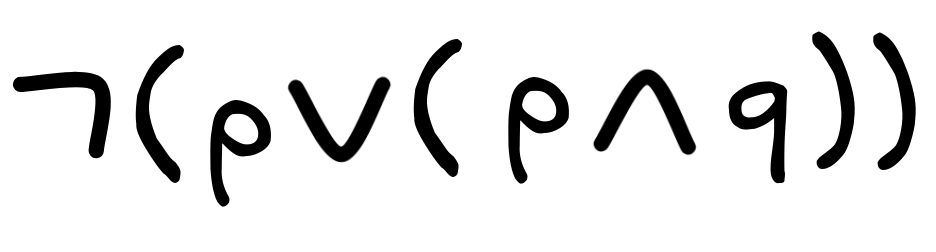into reverse Polish notation. Write step-by-step what the QUEUE is and what the STACK is. (2 points)

Transitivity of deductive inference

In the exercises for the chapter on valid inference, we showed that deductive inference is monotone, that is, adding additional premises preserves validity.

For this question, you’ll show that valid deductive inference is transitive. That is, you’ll show that if the inference from P to Q is deductively valid and the inference from Q to C is valid, then the inference from P to C is valid.

1. Formally state the property of transitivity using the symbol . (1 point)

2. Apply the definition of in terms of the propositions [P], [Q] , and [C] , the operation , and relation 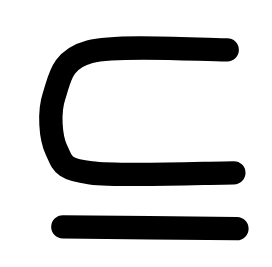to transform the claim it into a set theoretic claim. (1 point)

3. Suppose that S, T , and U are arbitrary sets. Show the following set-theoretic Theorem :

   

   Hint: Apply the definition of 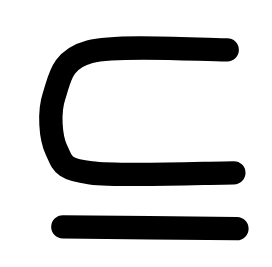and reason “step-by-step”:

   • 
   • 
   • Assume you have an arbitrary member of S , why must it be a member of U ?

   (2 points)

4. Conclude that the transitivity property holds. (1 point)