By: Johannes Korbmacher

FOL Inference

Having discussed the syntactic and semantic framework of FOL in Chapter 9. FOL , we’ll now turn to methods for step-wise inference in FOL.

As you’ll see, FOL inference packs a bit more of a punch than propositional inference: not only are the rules more complicated, but we have to be careful about how we apply them. The problem is that, because of undecidability, we can run into “loops” and “infinite regresses”. This problem is ultimately unavoidable, but there are methods and techniques to mitigate its consequences.

In this chapter, we’ll build on Section 7. Logical proofs , especially natural deduction . So if you’re not completely clear on the ideas from that chapter, go back and have another look.

Natural Deduction

Remember that natural deduction aims to mimic human-style step-by-step reasoning. This makes it a good starting point for our exploration of FOL inference.

The natural deduction system for FOL has four new rules in addition to the rules for the propositional connectives, two for each of the quantifiers $\forall,\exists$.

Let’s begin with the universal quantifier $\forall$. Here’s a straight-forward inference:

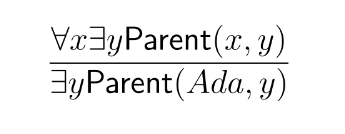
If everybody has a parent, then Ada does.

This inference is what lies behind the standard elimination rule for the universal quantifier:

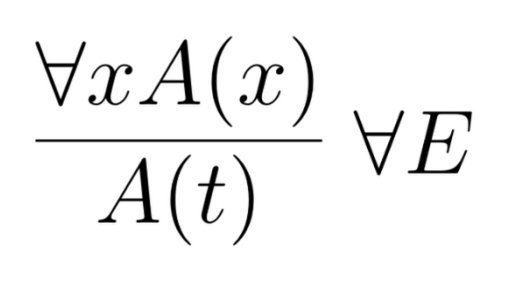
Here $A(t)$ stands for the result of replacing the variable $x$ with the term $t$ everywhere where $x$ is not “captured by” another quantifier:

Suppose $\forall xA(x)$ is $\forall x\exists y\mathsf{Parent}(x,y)$.
Then $A(x)$ is $\exists y\mathsf{Parent}(x,y)$.
If $t$ is $Ada$, then $A(t)$ is $\exists y\mathsf{Parent}(Ada,y)$.
NB: If $A(x)$ is

$$\exists y\mathsf{Parent}(x,y)\land \forall x\mathsf{Human}(x)$$

and $t$ is Ada, then $A(t)$ is

$$\exists y\mathsf{Parent}(Ada,y)\land \forall x\mathsf{Human}(x)$$

and not

$$\exists y\mathsf{Parent}(Ada,y)\land \forall x\mathsf{Human}(Ada)$$

This rule is also called universal instantiation, it formalizes the idea that if everything is so and so, then any thing you may pick is also so and so.

There is a small caveat: We may not chose $t$ completely freely in $\forall E$. The thing is that $t$ may not contain a variable $x$, which would be “captured” by another quantifier after. So, we may not, for example, infer:

$$\exists y\mathsf{Parent}(y,y)$$

from

$$\forall x\exists y \mathsf{Parent}(x,y).$$

We cannot infer from everyone having a parent that there’s somebody who’s their own parent.

This may seem “obvious”, but it’s important to keep in mind. The term $t$ may be a variable, but if may not be “captured” by another quantifier.

These kinds of side-conditions are par for the course in FOL.

This tells us what we can infer from a universally quantified claim, but from what can we infer a universally quantified claim itself?

The idea in natural deduction and much of the following is that we can use free variables for that, which are variables that are not “captured” by any quantifier. Take the statement:

$$\exists y\mathsf{Parent}(x,y)$$

In line with the reading of variables as pronouns, this says something like they have a parent, without specifying who “they” are. If we have established that they have a parent without having assumed anything else about who they are, we’ve effectively established for an arbitrary person that they have a parent. If we can show something like this, then we may infer that every person has a parent:

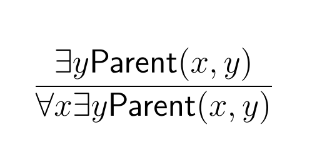
Expressed as a general inference rule, this becomes:

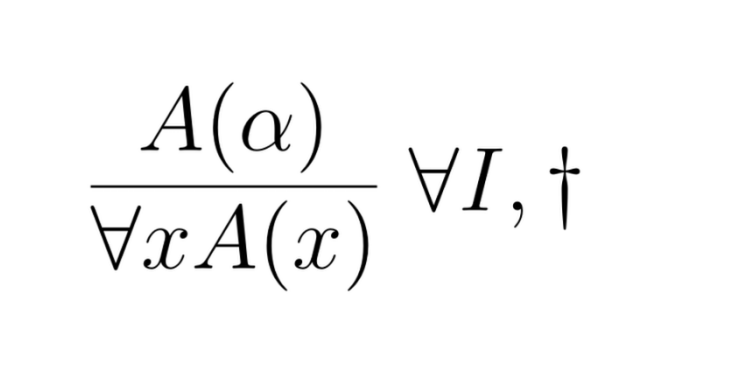
Here the $\alpha$ stands for an arbitrary variable $x,y,z,\dots$ subject to the following extremely important side-condition $\dagger$:

We may only infer $\forall xA(x)$ from $A(\alpha)$ if the variable $\alpha$ is really arbitrary. We ensure this by demanding that in no assumption, which occurs in the derivation before $A(\alpha)$ we may have $\alpha$ occurring unless its “captured” by a quantifier.

If we wouldn’t have this condition, we’d be saying that the following inference is valid:

$$\exists y\mathsf{Friend}(x,y)\vDash \forall x\exists y\mathsf{Friend}(x,y)$$

If they have a friend, then everybody has a friend. This is, of course, not a good inference: just because some person has friends, doesn’t mean everybody does.

The point is that we can only apply $\forall I$ if the variable doesn’t depend on anything else, so what would be OK, would be the following inference:

If everybody has a friend, then everybody either has a friend or is their own enemy.

Let’s turn to the existential quantifier $\exists$. As in the case of the universal quantifier $\forall$, there is a straight-forward inference that motivates our first inference rule.

Consider the following inference:

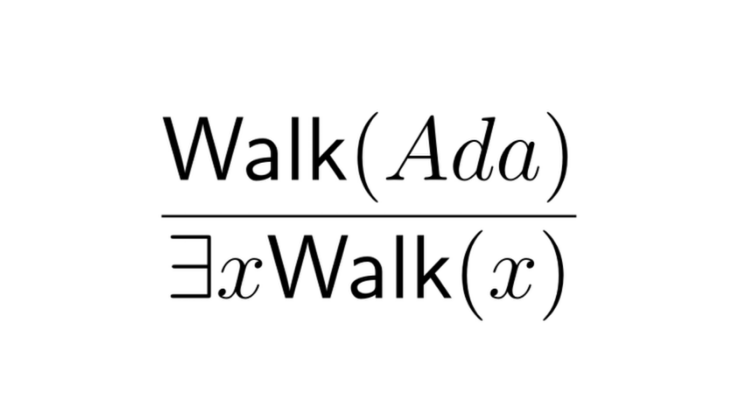
If Ada is on the Philosopher’s Walk, then somebody is on the philosophers walk.

If we abstract this to a general inference rule, we get:

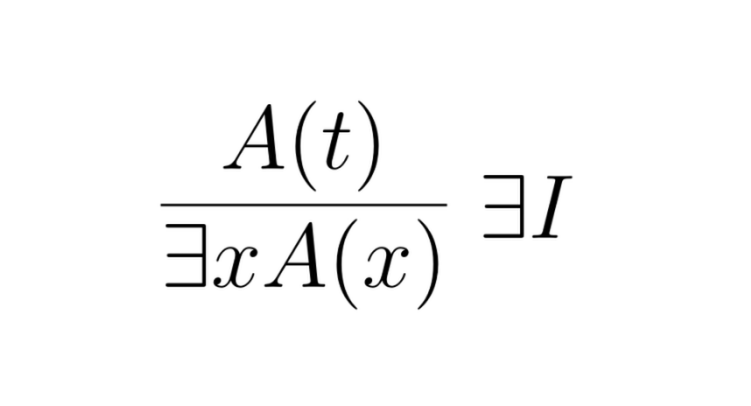
No side-conditions, not ifs and buts, that’s it 😃

This inference rule allows us to “introduce” an existential quantifier. But what can we infer from one?

The idea of natural deduction is to say that what follows from the claim that someone has a property is that some person, we don’t know who, has the property. Here’s how this work “in action”:

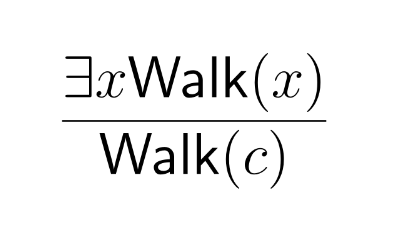
We’re just introducing a new constant $c$ for the person who’s on the Walk. It’s important that this constant doesn’t appear anywhere else in our derivation (or background knowledge base) to avoid serious mistakes.

For example, the following inference is (obviously) problematic:

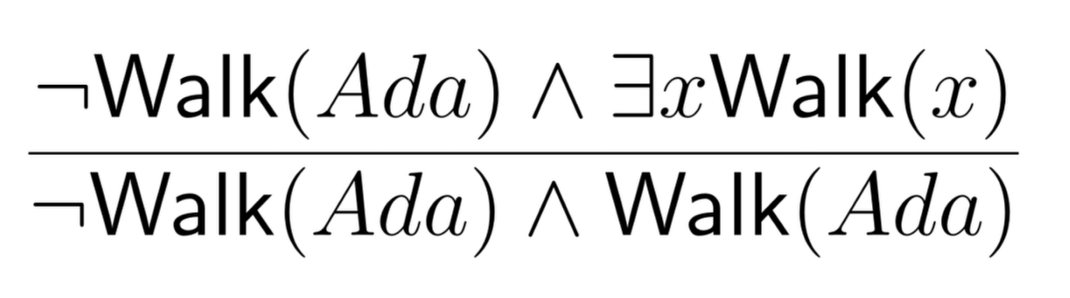
From Ada not being on the Walk but somebody being on the walk, we can’t infer that Ada is both on the walk and not.

The general rule, then, is the following:

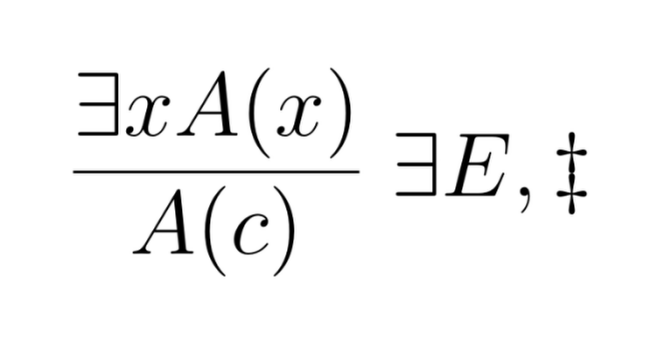
Here the side-condition $\ddagger$ says that the constant $c$ must be new to the inference (and knowledge base or any other background facts).

In a more complex reasoning setting, we would apply this rule as follows:

By adding the 4 rules we’ve just discussed to the rules for propositional logic, we obtain a proof system for FOL:

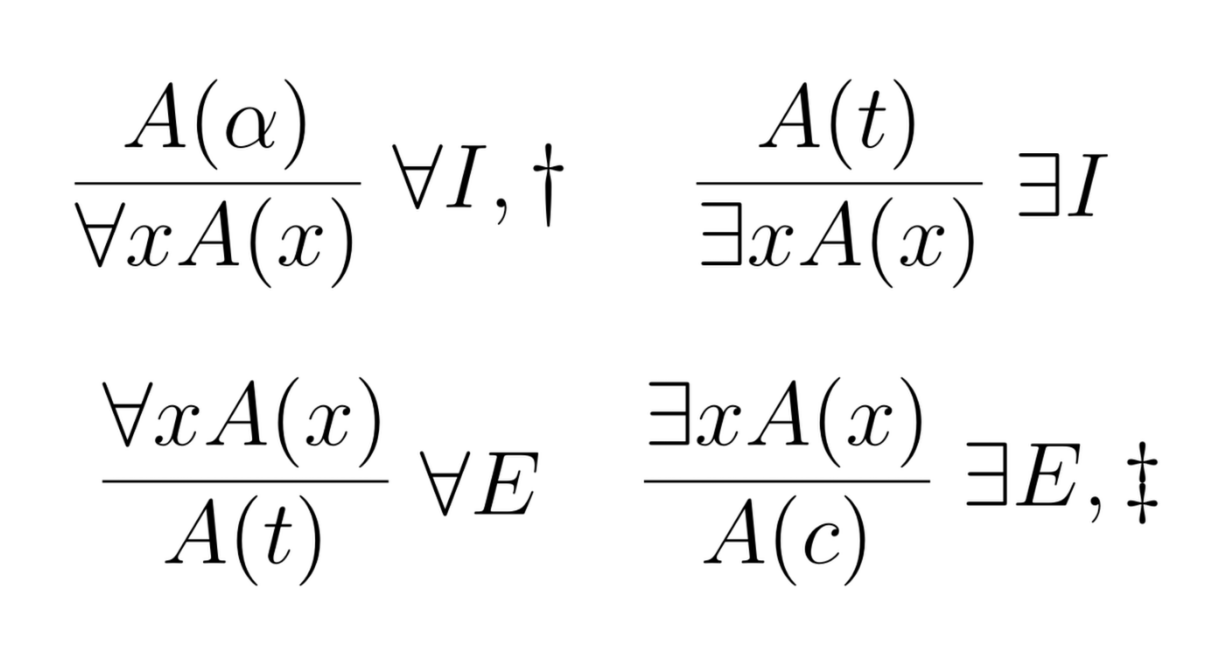
This system works™️, in the sense that it is sound and complete (with the definition from the previous chapter ).

Like any proof system for FOL, however, the systems is subject to undecidability: there cannot be any algorithm that in finite time correctly determines for arbitrary input inferences whether they’re valid.

This means, in particular, we can’t algorithmically search for proofs from a given premise set to a given conclusion and expect a yes/no answer (there is a proof/there isn’t a proof) after some finite time.

This is a fundamental problem for automated FOL inference, of course: any inference engine will need to be smart to be an effective reasoner, it can’t just brute force the problem. And even a smart algorithm may sometimes never find the answer.

The mathematical proof of this fundamental fact about reasoning is out of reach in this course, but we can illustrate why this happens. In fact, showing this is a great setup for the next topic:

Suppose that our premises contain a premise of the form:

$$\forall x\exists y\mathsf{BiggerThan}(x,y)$$

We want to know whether some conclusion follows from this. It doesn’t really matter what the potential conclusion is, since the problem already occurs if we automatically draw inferences from $$\forall x\exists y\mathsf{BiggerThan}(x,y)$$ in an unfortunate way.

Suppose we already have a constant in our knowledge base, say $0$ for the number zero. A natural thing to do is to instantiate any universal quantifier we come across with all the constants we know to see if we get the result. So, we infer $$\exists y\mathsf{BiggerThan}(0,y)$$ So far so good. Now, we don’t have any other constants, so we don’t draw any further inferences using $\forall E$. Since we’ve got nothing else we can do, we try the rule $\exists E$ and introduce a new constant: $c_1$ (you’ll see in a second why there’s an index):

$$\exists y\mathsf{BiggerThan}(0,c_1)$$

But wait, we’ve got a new constant, so we should infer:

$$\exists y\mathsf{BiggerThan}(c_1,y)$$

from

$$\forall x\exists y\mathsf{BiggerThan}(x,y)$$

Again, we’ve instantiated the $\forall$ with all our constants, so we try $\exists E$ again. Since our constant must be new, we choose $c_2$. Ah, a new constant, so we need to use $\forall E$ for our premise again, giving us:

$$\exists y\mathsf{BiggerThan}(c_1,c_2)$$

Now you quickly see that we’re caught in a infinite loop. Every time we instantiate the universal quantifier, the existential quantifier gives us a new constant to instantiate the universal quantifier for. This procedure gives us a bunch of proofs, but never the one we’re looking for.

Of course, we could avoid hitting the infinite loop “immediately” by first applying some other rules after we’ve introduced $c_1$. This would give us some more inferences, which is good of course. The problem, however, is that we can never completely avoid infinite loops like this. That’s the consequence of undecidability.

The moral of the story is that we need to be “smart” when we’re instantiating universal quantifiers: we need to instantiate them with the right terms and at the right time–otherwise we might get “stuck” in an infinite loop.

Making smart choices in this context is the topic of the next section.

Generalized MP and Unification

A standard setup we find ourselves in when it comes to automated FOL inference is that we have a KB with a bunch of rules of the form:

$$\forall x\forall y\dots((P_1(x,y,\dots)\land P_2(x,y,\dots))\land \dots \to C(x,y,\dots))$$

These are simple if-then rules (which correspond to Horn clauses).

Take, for example, the FOL version of the rules for our robot planning example: $$\forall x\forall n((On(x, n) \land Switch(x, n)) \to Off(x, n + 1))$$ $$\forall x\forall n((Off(x, n) \land Switch(x, n)) \to On(x, n + 1))$$

A straight-forward inference strategy to extract information from these clauses is to instantiate them and try to use modus ponens, effectively applying the forward chaining backward chaining techniques.

Suppose, for example, that we have the following information and want to know what this determines: $$On(L,1)$$ $$Switch(L,1)$$ We can then reason as follows (here in natural deduction):

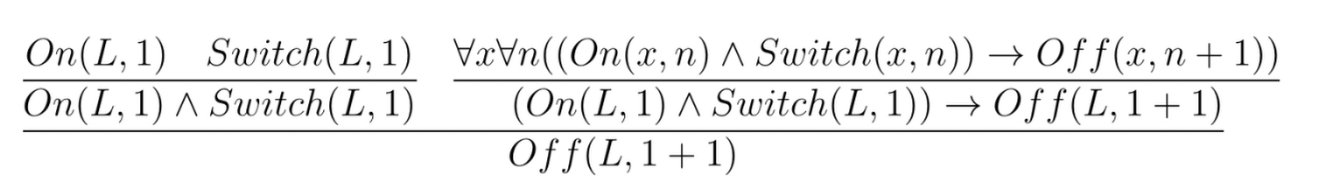
In this way, in two steps using $\land I$ and $\forall E$, we can infer that the left light will be off at time point $1+1=2$.

Once we recognize the pattern, we might want to be able to apply it directly as in the following:

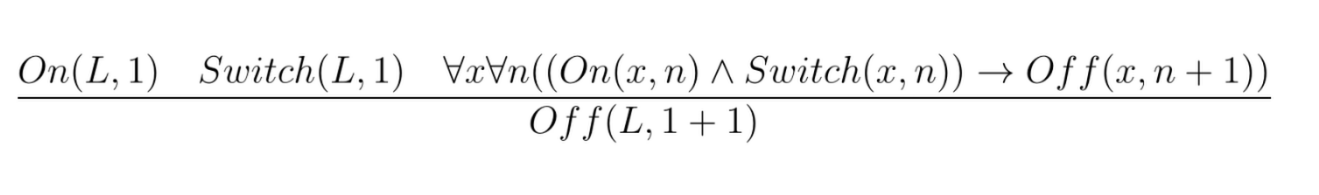
This can be achieved by adding the following generalized MP rule to our calculus (with the justification of being able to derive it using $\land I$ and $\forall E$):

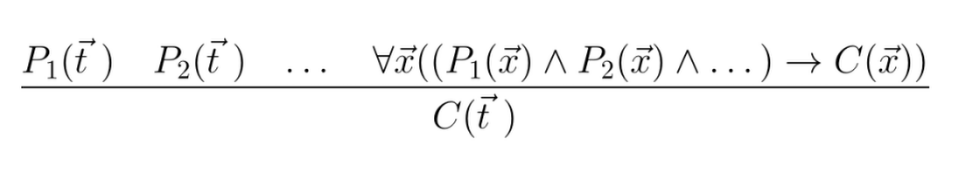
Here $\vec{t}=t_1,t_2,\dots$ and $\vec{x}=x_1,x_2\dots$ are abbreviations.

The generalized MP rule puts the focus a key questions for efficient FOL inference: choosing the right variables to instantiate universal quantifiers.

The point of inference pattern is to avoid unnecessary (but valid) instantiations when trying to apply universal instantiation.

To see whether we can apply generalized MP, we need to find an instantiation for the variables

$$x_1,x_2,\dots$$

such that applying it to

$$P_1(x_1,x_2,\dots)\land P_2(x_1,x_2,\dots)\land\dots$$

gives us

$$P_1(t_1,t_2,\dots)\land P_2(t_1,t_2,\dots)\land\dots$$

Here, it is clear what the answer is, viz:

$$x_1\mapsto t_1,x_2\mapsto t_2,\dots$$

But this example allows us to explain a key concept in FOL inference, which underlies most FOL inference algorithm. This concept is known as unification.¹

A unification procedure takes as input two formulas and gives as output a substitution of terms that makes the two formulas identical.

So, for example, if the input are the two formulas:

$$On(L,1)\land Switch(L,1)\qquad \text{ and } \qquad On(x,y)\land Switch(x,y)$$

the unification procedure would give as output:

$$x\mapsto L, y\mapsto 1$$

since substituting $L$ for $x$ and $1$ for $y$ everywhere, will turn the second input into the first.

Note that unification can be applied to two formulas where both need substitutions. Take, for example, the following two formulas as input:

$$\mathsf{YoungerThan}(x,Ada)\qquad \text{ and }\mathsf{YoungerThan}(Alan,y)$$

If we replace $x$ with $Alan$ in the first input and $y$ with $Ada$ in the second input, we obtain the unified clause

$$\mathsf{YoungerThan}(Alan,Ada)$$

Note also that there can be pairs of formulas that are not unifiable. Take, for example, the formulas $$\mathsf{OlderThan}(x,Alan)\qquad\mathsf{OlderThan}(Ada,x)$$ To unify the two formulas, we’d need to have both $x\mapsto Ada$ and $x\mapsto Alan$, which is impossible.

We use the notation $A[x_1\mapsto t_1,x_2\mapsto t_2,\dots]$ to denote the result of replacing $x_1$ with $t_1$, $x_2$ with $t_2$, and so forth everywhere those variables aren’t captured by quantifiers. This procedure is known substitution. We call the rule $x_1\mapsto t_1,x_2\mapsto t_2,\dots$ a substitution.

Using this notation, we can formulate the unification procedure as a procedure that gives us for two formulas $A,B$ a substitution $$[A,B]_{U}$$ such that $$A[A,B]_{U}=B[A,B]_{U}.$$

Using unification, we can write the generalized MP rule as follows:

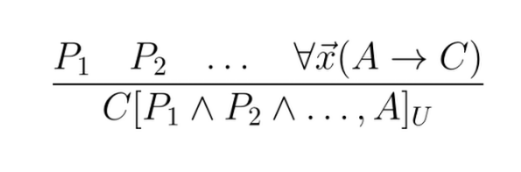
Using generalized MP, one can develop FOL versions of forwards and backwards chaining directly, side-stepping a search through all possible instantiations.

FOL resolution

A main limitation of the generalized MP rule is that it works only with universal conditions of the form we discussed above:

$$\forall x\forall y\dots((P_1(x,y,\dots)\land P_2(x,y,\dots))\land \dots \to C(x,y,\dots))$$

While these are very common in KBs, we often come across situations, where we’d like to apply FOL inference to arbitrary formulas.

A very effective and widely used technique for that is the generalization of the resolution method for FOL.

Remember that the resolution rule says that if you have two clauses

$$l_1\lor l_2\lor \dots\lor p \qquad \qquad \neg p\lor k_1\lor k_2\lor\dots$$

you can infer:

$$l_1\lor l_2\lor \dots k_1\lor k_2\lor\dots$$

In this rule $l_i,k_j$ are literals, meaning either propositional variables or their negations. How can we generalize this rule to the FOL case?

First, note that literals correspond to basic facts in propositional logic: $\mathsf{RAIN}$ is the basic fact that it rains, and $\neg\mathsf{RAIN}$ is the basic fact that it doesn’t. In fact, these basic facts directly correspond to the basic modeling facts $\nu(\mathsf{RAIN})=1$ and $\nu(\mathsf{RAIN})=0$. What are the corresponding basic facts in FOL?

The straight-forward answer is that they are atomic formulas and their negations, like:

$$\mathsf{OlderThan}(\mathsf{FatherOf}(Ada),Ada)\qquad \neg\mathsf{OlderThan}(\mathsf{FatherOf}(Ada),Ada)$$

Using these, we can, for example, formulate valid, resolution-style inferences like the following:

If we have complex FOL formulas, which are just build up from atoms using $\neg,\land,\lor,\to$, we can straight-forwardly generalize the propositional procedure to the FOL case: simply re-write the formula in CNF (following the procedure laid out in chapter 5.3 ), and we can apply the resolution rule.

For example, the above application of the resolution rule shows the validity of the following FOL inference:

$$\mathsf{Parent}(\mathsf{FatherOf}(Ada),Ada)\to \mathsf{OlderThan}(\mathsf{FatherOf}(Ada),Ada),$$ $$\mathsf{OlderThan}(\mathsf{FatherOf}(Ada),Ada)\to$$ $$\mathsf{Before}(\mathsf{BirthdayOf}(\mathsf{FatherOf}(Ada)),\mathsf{BirthdayOf}(Ada))\vDash$$ $$\mathsf{Parent}(\mathsf{FatherOf}(Ada),Ada)\to$$ $$\mathsf{Before}(\mathsf{BirthdayOf}(\mathsf{FatherOf}(Ada)),\mathsf{BirthdayOf}(Ada))$$

It turns out that universal quantifiers are relatively easy to handle using a simple “trick”. We simply treat “free” variables, that is variables which are not captured by a corresponding quantifier, as implicitly quantified. To illustrate, consider the following example.

We want to check the validity of the following inference: $$\forall x\forall y(\mathsf{Parent}(x,y)\to \mathsf{OlderThan}(x,y)),$$ $$\forall x\forall y(\mathsf{OlderThan}(x,y)\to \mathsf{Before}(\mathsf{BirthdayOf}(x),\mathsf{BirthdayOf}(y)))\vDash$$ $$\forall x\forall y(\mathsf{Parent}(x,y)\to \mathsf{Before}(\mathsf{BirthdayOf}(x),\mathsf{BirthdayOf}(y)))$$ We do this with the following application of the resolution rule:

Several things have happened here:

We’ve dropped all the universal quantifiers. Along the way, we made sure to rename all variables in such a way that every formula has unique variables.
We re-wrote the resulting quantifier free formulas in using the re-writing rules.
We applied the resolution rule using a substitution where $u\mapsto x$ and $v\mapsto y$. The first and third steps are the crucial things to focus on here: we allow a resolution application with atoms $$\mathsf{OlderThan}(u,v)$$ and $$\neg\mathsf{OlderThan}(x,y).$$ This is the way in which we treat the free variables $x,y,u,v$ as “implicitly quantified”. We think of them as being able to assume different values, in particular $x$ and $u$ and $y$ and $v$ can assume the same values, which makes this an ordinary case of resolution.

But when doing so, we must respect the new assignment of variables. That is, we apply the substitution $u\mapsto x,v\mapsto y$ to the entire formula, giving us the conclusion.

Note that $[u\mapsto x,v\mapsto y]$ is a unification for the formulas $\mathsf{OlderThan}(u,v)$ and $\neg\mathsf{OlderThan}(x,y).$ This gives us the most general form of the FOL resolution rule:

$$l_1\lor l_2\lor \dots\lor m \qquad \qquad \neg n\lor k_1\lor k_2\lor\dots$$

you can infer:

$$(l_1\lor l_2\lor \dots k_1\lor k_2\lor\dots)[m,\neg n]_U$$

This is the resolution rule we’ve applied in the inference:

To make this a general inference rule, we allow the $m,\neg m$ pair to occur anywhere within $l_1\lor l_2\lor \dots\lor m, \neg n\lor k_1\lor k_2\lor\dots$ respectively (not only at the end/beginning).

It turns out that we can describe a general FOL inference procedure using resolution. This involves FOL variant of the CNF from chapter 5.3 .

We first describe the procedure. To transform an arbitrary formula into FO-CNF:

Re-write all conditionals using the rule: $A\to B\leadsto \neg A\lor B$
Use the de Morgan rules to move all negations inwards, i.e. apply the rules:
- $\neg\neg A\leadsto A$
- $\neg(A\land B)\leadsto \neg A\lor\neg B$
- $\neg(A\lor B)\leadsto \neg A\land\neg B$.
Use the quantifier negation rules to move negations inwards via the following rules:
- $\neg\forall xA\leadsto \exists x\neg A$
- $\neg\exists xA\leadsto \forall x\neg A$
Re-name the variables such that each quantifier has its own variable, so that, e.g. $\forall xA\land \exists xB\leadsto \forall x_1A\land \forall x_2B$.
For each quantifier, apply the following procedure known as Skolemization:²
- Eliminate the quantifier from the formula and replace the variable it quantifiers over with a function symbol $f_i(x_j,x_k,\dots)$, where: $x_i$ is the variable the universal quantifier used and $x_j,x_k,\dots$ are all the universally quantified variables that come before $x_i$ in the formula.
- For example, $\forall x\exists y(P(x)\to R(x,y))$ becomes $\forall x(P(x)\to R(x,f(x)))$.
Drop all the remaining universal quantifiers.
Apply the distribution law:
- $A\lor (B\land C)\leadsto (A\lor B)\land (A\lor C)$

We apply all these steps recursively until we’ve got a formula in CNF.

For example, here’s what the procedure does to the formula $$\forall x\forall y(\mathsf{Parent}(x,y)\to \neg \forall z (\mathsf{Parent}(z,y)\to x=z))$$

$\forall x\forall y(\neg \mathsf{Parent}(x,y)\lor \neg\forall z(\neg \mathsf{Parent}(z,y)\lor x= z))$ (Re-write conditionals)
$\forall x\forall y(\neg \mathsf{Parent}(x,y)\lor \exists z\neg (\mathsf{Parent}(z,y)\land x= z))$
$\forall x\forall y(\neg \mathsf{Parent}(x,y)\lor \exists z\neg (\neg\mathsf{Parent}(z,y)\lor x= z))$
$\forall x\forall y(\neg \mathsf{Parent}(x,y)\lor \exists z(\neg \neg\mathsf{Parent}(z,y)\land x\neq z))$
$\forall x\forall y(\neg \mathsf{Parent}(x,y)\lor \exists z(\mathsf{Parent}(z,y)\land x\neq z))$
$\forall x\forall y(\neg \mathsf{Parent}(x,y)\lor (\mathsf{Parent}(f(x,y),y)\land x\neq f(x,y)))$
$\neg \mathsf{Parent}(x,y)\lor (\mathsf{Parent}(f(x,y),y)\land x\neq f(x,y))$
$(\neg \mathsf{Parent}(x,y)\lor \mathsf{Parent}(f(x,y),y))\land (\neg \mathsf{Parent}(x,y)\lor x\neq f(x,y)))$

The CNF procedure always leads to a formula that is in CNF from the perspective of propositional logic. Crucially, however, the formula is not necessarily equivalent to the original formula in FOL. It is what’s called equi-satisfiable: the re-written formula is satisfiable (has a model) if and only if the original formula has a model.

This is because of the Skolemization involved, but we won’t go into the mathematical details here. The crucial thing is that the procedure gives us a formula, which is in CNF and doesn’t involve quantifiers. For $A$ a formula, we denote the result of applying the above procedure by $CNF(A)$.

Since the formula $CNF(A)$ is equi-satisfiable with the original formula $A$, we can apply the resolution technique to determine the transformed formula’s satisfiability and infer the satisfiability status of the original formula. This, it turns out, gives us a sound and complete inference system.

From here on out the ideas are actually just what we know from propositional logic (compare Chapter 7.2.3 ):

To test an inference $$P_1,P_2,\dots\vDash C$$ for validity, we test whether the formula $$P_1\land P_2\land \dots\land \neg C$$ is satisfiability.
We do this by applying the resolution rule as many times as possible to the clauses of $$CNF(P_1\land P_2\land \dots\land \neg C).$$
If we can derive $\bot$, the inference is valid, if we cannot, the inference is invalid.

The procedure we’ve just sketched leads to a very effective way of automated reasoning, which provides the basis for many ATPs.

FOL Inference

Natural Deduction

Generalized MP and Unification

FOL resolution

Further readings