By: Johannes Korbmacher
Many-valued logics
In this chapter, you’ll learn for the first time about some non-classical logics. Specifically, we’ll leave behind the modelling assumption of classical logic that there are just the two truth-values $0,1$. In other words, in this chapter you’ll learn about many-valued logics.
After briefly talking about syntax, we’ll discuss two different families of many-valued logics, with different motivations and applications in AI:
- the 3-valued Kleene and Łukasiewicz logics,
- the infinitely valued fuzzy logics.
The chapter mainly focuses on semantics to illustrate the underlying ideas and models of the world that motivate the relevant logics. Inference in many-valued logics will be a topic for the exercises.
Syntax
In this chapter, we’ll be working in propositional contexts only.
For much of the chapter, we’ll assume that our language is a propositional language with $n$ propositional variables, $p_1, \dots, p_n$, and only the connectives $\neg,\land,\lor$. That is, the BNF of our language is:
$$\langle prop\rangle::= p_1\mid \dots\mid p_n$$
$$\langle fml\rangle::=\langle prop\rangle\mid\neg\langle fml\rangle\mid (\langle fml\rangle\land \langle fml\rangle)\mid (\langle fml\rangle\lor \langle fml\rangle)$$
For concreteness sake, we’ll use concrete propositional constants, like $\mathsf{RAIN}$ or $\mathsf{SUN}$ like before.
At points, we’ll turn to the conditional $\to$, which will be important to formula rules for many-valued knowledge bases, for example.
In fuzzy logics, in particular, it’s common to introduce additional operators on top of the usual ones. In basic fuzzy logic (BL), for example, which we won’t cover in this chapter since—despite its name—is more complicated than other systems, we have two conjunction operators: strong conjunction $\otimes$ and weak conjunction $\land$. In fact, in BL, we typically take $\otimes$ to be the primitive operator and treat the “normal” $\land$ as defined using $\otimes,\to$ via the rule: $$A\land B=A\otimes (A\to B).$$
It’s an interesting exercise to check that in a classical, Boolean setting, $$A\land B$$ and $$A\land (A\to B)$$ are logically equivalent. It is important to note, however, that in non-classical settings, the logical laws may be different.
In this chapter, however, we try to avoid non-classical syntax as much as possible in order to focus on non-classical, many-valued semantics.
Kleene and Łukasiewicz logics
The logics of Kleene and Łukasiewicz which we’ll look at in this section are examples of 3-valued logics. That is, when it comes to semantics we’ll not only have $0,1$ as possible values, but an additional third truth-value.
From a technical perspective, it doesn’t matter which symbol we use to represent the third truth-value, but in this chapter, we’ll use $i$. One reason for this choice is the motivation behind Kleene and Łukasiewicz’s logics: the idea that some statements can have an indeterminate truth-value.
Think, for example, about the claim that $\mathsf{RAIN\_TOMORROW}$ it rains tomorrow. What truth-value does it have now? We might have evidence for or against it raining tomorrow: the forecast, the way the weather is today, information about air pressure, temperature, and so on. But ultimately, these only lead to a probability of rain tomorrow. Unless we’re strong determinists, we may very well believe that the truth-value of $\mathsf{RAIN\_TOMORROW}$ is not decided yet, it is indeterminate.
This concept finds many important applications in AI. To begin with, any AI that reasons in the “real world” will encounter indeterminacy as in our example. But more concretely, we often encounter cases like this when querying databases or knowledge bases.
What, for example, should happen when we query a KB and the KB doesn’t contain the answer? We’ve encountered this with backward chaining in Chapter 6. Logical conditionals . Back then, we applied the closed-world assumption (CWA), which says that non-derivable statements as false.
But in many situations that’s not what we want: imagine an AI expert system for weather prediction, which doesn’t have enough information to predict the weather tomorrow. We don’t want to conclude from this that $\mathsf{RAIN\_TOMORROW}$ is false. It may turn out true, it may turn out false… we don’t know. It’s current truth-value is indeterminate. The open-world assumption allows us to do just that.
Another example of a similar kind is provided by the Structured Query Language
(SQL), which is one of the standard
languages for relational database
management
and behind much of the internet’s
backend. In SQL, when a
query doesn’t return a result because of the absence of data, it returns the
SQL null, which is essentially our
third truth-value $i$. Moreover, when null returns as part of a complex
query, SQL applies what’s effectively Kleene’s 3-valued logic.
Semantics
So how can we reason with 3 truth-values. We’ll take the semantic perspective here and explain how to provide a 3-valued semantics for a propositional language $\mathcal{L}$ with connectives $\neg,\land,\lor$. This gives as a notion of valid inference $\vDash$ in 3-valued logic, which we can then use in AI applications.
The logic we describe here first is what’s known as (strong) Kleene logic.1
First, we need to adjust the notion of a valuation. In Boolean algebra, a valuation valuation was a function $$\nu:\langle prop\rangle\to\Set{0,1}.$$ In this chapter, instead, a valuation will simply be a function $$\nu:\langle prop\rangle\to\Set{0,i,1}.$$
Just like in Boolean algebra, we can think of a valuation as a model of a logically possible situation, where $$\nu(\mathsf{RAIN\_TOMORROW})=1$$ means that according to $\nu$ it will rain tomorrow, $$\nu(\mathsf{RAIN\_TOMORROW})=0$$ means that according to $\nu$ it won’t rain tomorrow, and $$\nu(\mathsf{RAIN\_TOMORROW})=i$$ means that according to $\nu$ it’s indeterminate whether it will rain tomorrow.
Next, we generalize our truth-function to the 3-valued setting. Remember that a Boolean truth-function is simply a function from Boolean truth-values to Boolean truth-values. Correspondingly, a 3-valued truth-function is a function that takes any of our 3 truth-values as input and gives one of the 3-values as output.
Just like in Boolean algebra, we have 3 truth-functions that interpret the connectives:
-
The 3-valued negation function:
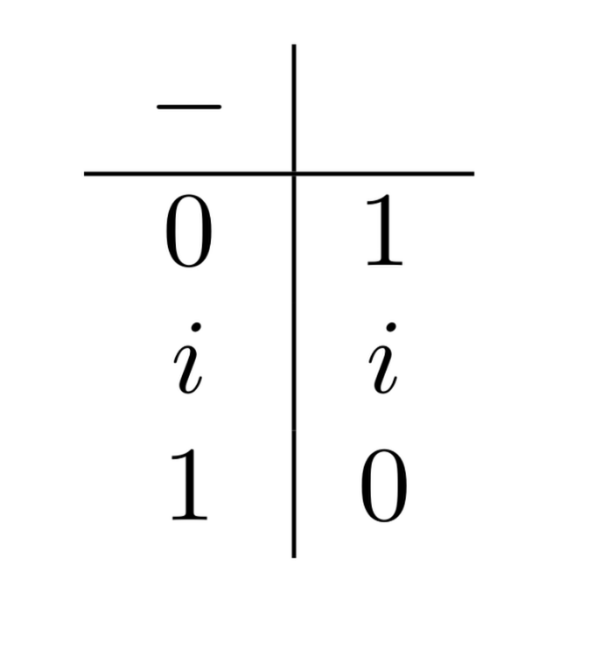
-
The 3-valued conjunction function:
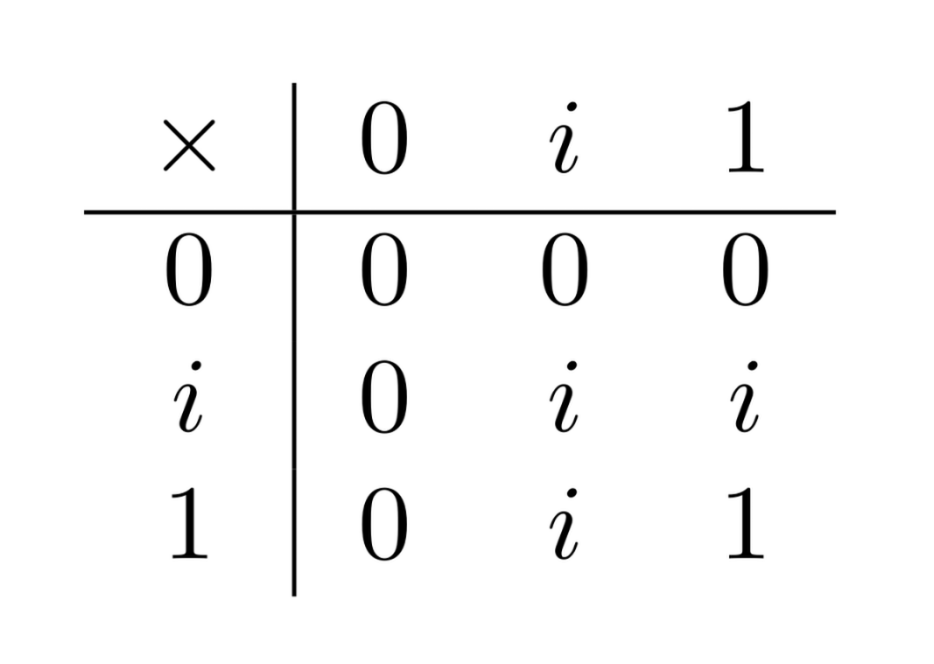
-
The 3-valued disjunction function:
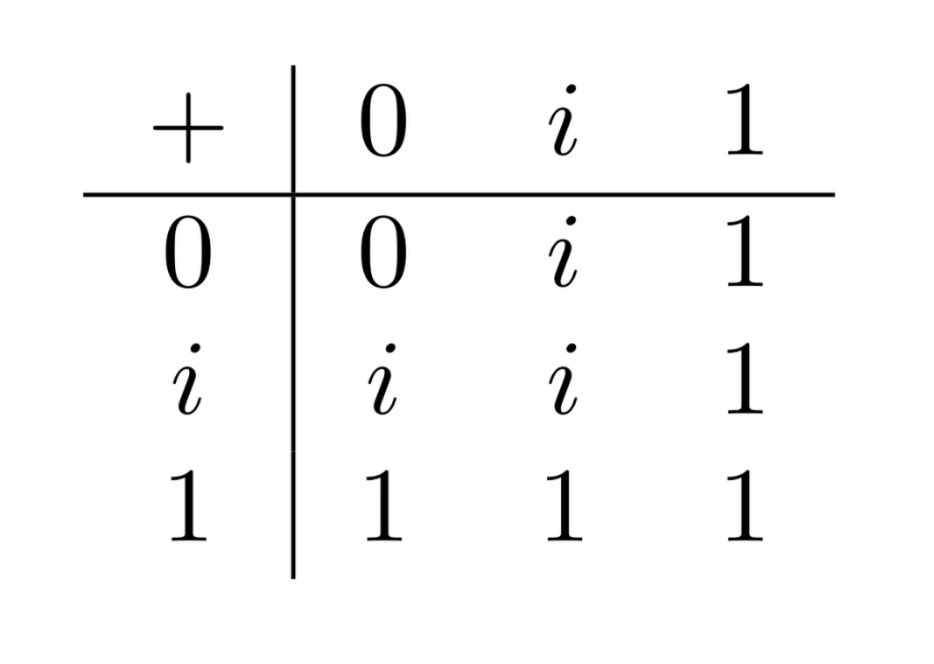
These truth-tables are build on the idea that $i$ stands for an “unsettled” classical truth-value. For example, $1\times i = i$ because if $i$ would turn out to be $1$, then we’d have $1\times 1=1$ but if $i$ turns out to be $0$, then we’d have $1\times 0=0$. So $1\times i$ is unsettled itself.
Instead, we have $0\times i=0$ since the value of $i$ doesn’t matter to see that the conjunction must be false. If $i$ turned out to be $1$, we’d have $0\times 1=0$, and if $i$ turned out to be $0$, we’d have $0\times 0=0$. Either way, we get $0$, which is why we say $0\times i=0$.
We can now use these truth-functions to recursively define truth in a valuation in the same way we did it in Boolean algebra:
$$\nu(\neg A)=-\nu(A)$$ $$\nu(A\land B)=\nu(A)\times \nu(B)$$ $$\nu(A\lor B)=\nu(A)+\nu(B)$$
Just that now the truth-functions $-,\times,+$ are 3-valued.
Somewhat surprisingly, even the definition of valid inference remains the same—we just applied in a 3-valued setting.
First, we define the $[A]$ of a formula $A$ to be: $$[A]:=\Set{\nu:\nu(A)=1}.$$ Put in words, this means that the content of $A$ is the set of valuations/models, which assign to $A$ the truth-value $1$. We then say:
$$P_1,P_2,\dots\vDash C\Leftrightarrow [P_1]\cap [P_2]\cap \dots\subseteq [C]$$
Many inference that are classically valid remain valid in Kleene logic. Remember, for example our proof of concept inference from Chapter 4 :
$$\mathsf{RAIN}\lor \mathsf{BIKE},\neg\mathsf{RAIN}\vDash\mathsf{BIKE}$$
The reasoning to show that this inference is valid works exactly like that in Kleene logic.
Let’s check out the relevant valuations:
The members of $[\mathsf{RAIN}\lor \mathsf{BIKE}]$ are:
all valuations $\nu$ with $\nu(\mathsf{RAIN})=1$
all valuations $\nu$ with $\nu(\mathsf{BIKE})=1$
The members of $[\neg\mathsf{RAIN}]$ are such that $\nu(\mathsf{RAIN})=0$
Since we can’t have $\nu(\mathsf{RAIN})=0$ and $\nu(\mathsf{RAIN})=1$, we know that the members of $[\mathsf{RAIN}\lor \mathsf{BIKE}]\cap [\neg\mathsf{RAIN}]$ are only the ones that $\nu(\mathsf{BIKE})=1$.
But that means that $$[\mathsf{RAIN}\lor \mathsf{BIKE}]\cap [\neg\mathsf{RAIN}]\subseteq [\mathsf{BIKE}],$$ as desired.
So, what changes?
Kleene laws
It turns out that almost all the Boolean laws also hold in Kleene logic. It’s easier to say which ones don’t.
Of the one’s we listed in chapter 4 , it’s just the following two which fail:
| Negation laws | ||
|---|---|---|
| Complementation 1 | $x\times -x=0$ | |
| Complementation 2 | $x+ -x=1$ | |
To see this, just plug in $i$ for $x$ in the equations:
$$i\times -i=i\times i=i$$
$$i+-i=i+i=i$$
The main consequence of the failure of these two laws is that Kleene logic has no logical truth. In Boolean logic, we have, for example:
$$\vDash \mathsf{RAIN\_TOMORROW}\lor\neg \mathsf{RAIN\_TOMORROW}$$
This means, of course, that the formula get’s value $1$ in all models, it’s a logical truth—of Boolean logic. In Kleene logic, it’s easy to find a valuation, where the formula is not true. Just assign:
$$\nu(\mathsf{RAIN\_TOMORROW})=i$$
We get:
$$\nu(\mathsf{RAIN\_TOMORROW}\lor\neg \mathsf{RAIN\_TOMORROW})=i$$
Under the open world assumption, this is exactly as it should be: whether it rains tomorrow or not is an open question, it’s not settled one way or the other.
Whether the absence of logical truths is a problem or not is a matter of debate. But here’s a reason for thinking why in many AI applications it’s not:
When we’re developing an AI capable of learning the starting assumption is that there are things that it doesn’t know. Correspondingly, the AI shouldn’t make any assumptions about what the world is like with respect to the things it doesn’t know, it should be a tabula rasa. The failure of the Boolean laws is an example of just that: the AI doesn’t know whether it rains tomorrow or not. That’s the point!
Łukasiewicz logic
The difference between Kleene’s and Łukasiewicz’s logic just concerns the treatment of the logical conditional in 3-valued logic.
Remember the Boolean truth-table for the conditional:
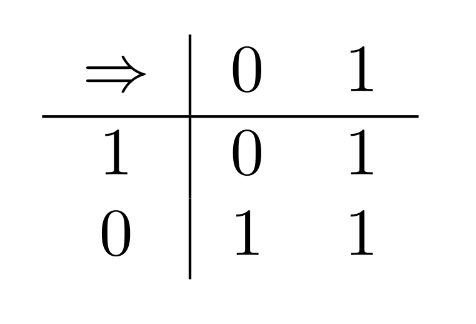
How should we generalize this to a 3-valued setting?
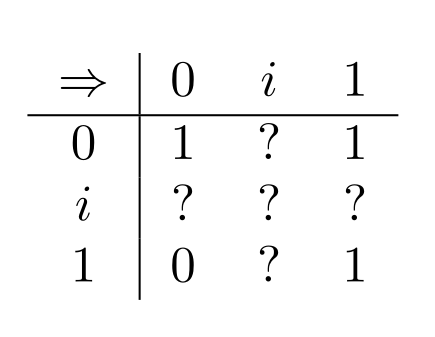
Kleene uses the standard rationale of reading $i$ as an unsettled classical truth-value, which gives us:
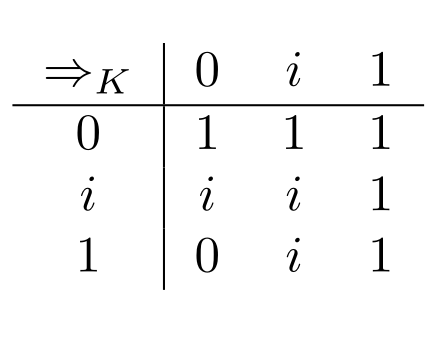
This truth-table recovers the Boolean logical equivalence between $A\to B$ and $\neg A\lor B$ in our 3-valued setting. But it faces a problem.
Consider the conditional:
$$\mathsf{RAIN\_TOMORROW}\to \mathsf{RAIN\_TOMORROW}$$
This sounds plausible even if we think that it’s not settled whether it rains tomorrow: if it does rain, it rains.
But on Kleene’s table for $\Rightarrow$, it’s possible to give this formula the value $i$. Just set:
$$\nu(\mathsf{RAIN\_TOMORROW})=i$$
You get:
$$\nu(\mathsf{RAIN\_TOMORROW}\to \mathsf{RAIN\_TOMORROW})=i\Rightarrow_K i=i$$
Łukasiewicz’s thought is that this is unsatisfactory, treating $A\to A$ as a logical law doesn’t make any substantial assumptions about the world. So we should adjust our table to make it a law. It turns out that this is possible, without introducing additional problems by setting:
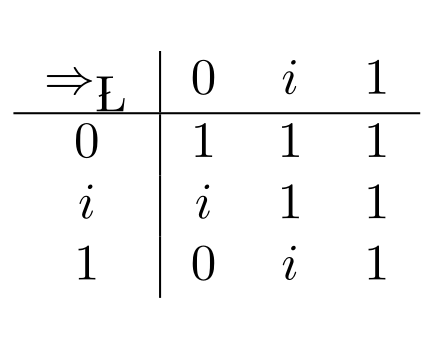
This table gives us:
$$\vDash\mathsf{RAIN\_TOMORROW}\to \mathsf{RAIN\_TOMORROW}$$
It’s easy to check this by considering the possible truth-values for $\mathsf{RAIN\_TOMORROW}$:
-
If $\nu(\mathsf{RAIN\_TOMORROW})=0$, then $\nu(\mathsf{RAIN\_TOMORROW}\to \mathsf{RAIN\_TOMORROW})=0\Rightarrow_{Ł} 0=1$
-
If $\nu(\mathsf{RAIN\_TOMORROW})=i$, then $\nu(\mathsf{RAIN\_TOMORROW}\to \mathsf{RAIN\_TOMORROW})=i\Rightarrow_{Ł} i=1$
-
If $\nu(\mathsf{RAIN\_TOMORROW})=1$, then $\nu(\mathsf{RAIN\_TOMORROW}\to \mathsf{RAIN\_TOMORROW})=1\Rightarrow_{Ł} 1=1$
The table for $\Rightarrow$ marks the only difference between Kleene’s and Łukasiewicz’s logics. These differences mainly play a role when we’re trying to formula rules for 3-valued systems.
Fuzzy logics
Having seen a fruitful approach to indeterminacy, we’ll turn to a different issue that motivates abandoning the bivalence assumption: vagueness.
Take, for example, the statement $$\mathsf{WARM}.$$ We might come across this in the context of a weather forecast system, as in the previous section. When should our system judge this statement as true?
Clearly, at 0℃ , the statement is false. And at 30℃ the statement is clearly true. But what at 20℃ ? It doesn’t seem to be clear where the cut-off point is. Suppose you think it needs to be at least 20℃ to be warm, but 20℃ is warm. What about At 19.8℃ , then? There is almost no perceivable difference between the two temperatures, but we just said one is warm the other is cold.
There doesn’t seem to be a clear “cutoff point” between warm and not: the concept is vague.2 Classical propositional logic cannot easily handle vague concepts: in classical logic $\mathsf{WARM}$$, for any given possible situation, it is either warm or not. In other words, there is a clear cut-off point across all possible situations.
Fuzzy logic is an approach to valid inference involving vague concepts, which models vagueness by using real numbers between 0 and 1 (from the so-called unit interval) instead of truth-values.
For example, a fuzzy logician could assign to $\mathsf{WARM}$:
-
At 30℃ a value close to 1.
-
At 20℃ a value around 0.7.
-
At 18℃ a value around 0.6.
-
At 10℃ a value around 0.2.
-
At 0℃ the value 0.
This approach is then extended to handle complex vague concepts, like $$\mathsf{WARM}\land\mathsf{HUMID},$$ and the like. This is the topic we’ll be looking into in this section.
Fuzzy logic has had a significant impact on AI. After Lotfi Zadeh introduced the AI/computer science community, the approach took off mainly in Japanese research and development, where many so-called fuzzy control systems were developed. These concerned logic-based AI systems, ranging from AC units over camera autofocus to the automated controls for subway lines.
These systems involve fuzzy rules which relate two vague concepts in the form of a (fuzzy) logical conditional. For example, an AC unit might involve the fuzzy rule:
- IF $\mathsf{WARM}\lor\mathsf{HUMID}$ THEN $\mathsf{POWER}$
That is, if it’s either warm or humid, then the unit should power on. The crucial thing is that the connection between the concepts $\mathsf{WARM}$ and $\mathsf{HUMID}$ on the one side and $\mathsf{POWER}$ on the other side is itself fuzzy.
There are many different ways of implementing this, but the most straight-forward and common way is to interpret the rule as saying that to the extend that the antecedent holds, the consequent should hold. That is the rule says that if $\mathsf{WARM}\lor\mathsf{HUMID}$ has value 0.7, then $\mathsf{POWER}$ should also have 0.7.
These kinds of rules have lead to the development of extremely efficient automated systems, which outperform human-operated systems but also classical-logic based systems by large margins.
Let’s look at how this works.
Ł
There are many different systems of fuzzy logic. In this section, we’ll look at a system that has, in fact, for the first time been described by Łukasiewicz (even before the term “fuzzy logic” was introduced by Zadeh). Hence the systems is called Ł. It is one of the simpler systems that lines up nicely with the systems we’ve discussed previously It is one of the simpler systems that lines up nicely with the systems we’ve discussed previously.
We’ll focus on propositional logic with $\neg,\land,\lor$.
First, let’s introduce fuzzy valuations, that is functions $$\nu:\Set{p_1,p_2,\dots}\to [0,1],$$ where $p_1,p_2,\dots$ are our propositional varibles and $[0,1]$ is the unit interval of numbers between 0 and 1.
The idea is, like before, that a valuation models a possible situation, now involving a fuzzy/vague concept. So, using the concept of warmth from before, we could say that
- $\nu(\mathsf{WARM})=1$ describes the situations with over 30℃ .
- $\nu(\mathsf{WARM})=0.7$ describes situations with 20℃
- $\nu(\mathsf{WARM})=0.6$ describes situations with 18℃
- $\nu(\mathsf{WARM})=0.2$ describes situations with 10℃
- $\nu(\mathsf{WARM})=0$ describes situations with below 0℃
The notion of a fuzzy truth-function, then, is just the notion of functions from fuzzy truth-values to fuzzy truth-values: from the unit interval to itself.
How should the fuzzy truth-functions for our connectives behave? In Ł, we abandon the previous notation of $-,\times,+$ for the truth-functions, since they are no longer helpful mnemonics. We rather write $f_\neg,f_\land,f_\lor$ for the truth-functions corresponding to $\neg,\land,\lor$.
There are different possible answers to the question of how the fuzzy values of $\neg A, A\land B,A\lor B$ depend on the values of $A,B$. The most general theory involves so-called t-norms. The system Ł is just a special case of this, but it’s particularly easy to understand.
In Ł, we use the following truth-functions:
$$f_\neg(x)=1-x$$ $$f_\land(x,y)=min(x,y)$$ $$f_\lor(x,y)=max(x,y)$$
Here the $min$ and $max$ functions pick the smaller or bigger of two numbers, respectively.
These functions, then, recursively interpret the operators as usual:
$$\nu(\neg A)=f_\neg(\nu(A))$$ $$\nu(A\land B)=f_\land(\nu(A),\nu(B))$$ $$\nu(A\lor B)=f_\lor(\nu(A),\nu(B))$$
So, if, for example, we have: $$\nu(\mathsf{WARM})=0.7$$ $$\nu(\mathsf{HUMID})=0.4$$ That is, if it’s somewhat warm and more dry than humid. Then, we’d get: $$\nu(\mathsf{WARM}\lor\mathsf{HUMID})=0.7$$ That is, it’s somewhat warm or humid.
Why should we pick these fuzzy truth-functions and not some others? Here’s one motivation (which may work in some situation but not in others). We can (but don’t have to) interpret $\nu(\mathsf{WARM})=0.5$ as an indeterminate state with respect to warmth—it’s neither warm nor not warm.
It turns out that under this reading, the Ł truth-functions are just a generalization of the Kleene truth-functions: if we restrict the inputs of $f_\neg,f_\land,f_\lor$ to the set $\Set{0,0.5,1}$, they are the Kleene functions $-,\times,+$ from before.
Valid inference, in Ł, is modelled after the idea of fuzzy rules. We generalize the idea of truth preservation, which we’ve used so-far to model valid inference and apply the idea of truth-degree preservation by saying that an inference $P_1,\dots,P_n\vDash C$ is valid just in case for every valuation $\nu$, the value $\nu(C)$ is bigger than the smallest value of $\nu(P_1),\dots,\nu(P_n)$. More mathematically, we say:
$$P_1,P_2,\dots\vDash C$$ $$\Leftrightarrow$$ $$\text{for all }\nu, min(\nu(P_1),\dots,\nu(P_n))\leq \nu(C)$$
This definition gives us the validity of various inferences. For example, we have:
$$\mathsf{WARM}\vDash\mathsf{WARM}\lor\mathsf{HUMID}$$
This is because $\nu(\mathsf{WARM}\lor\mathsf{HUMID})=max(\nu(\mathsf{WARM}),\nu(\mathsf{HUMID}))$ and $$\nu(\mathsf{WARM})\leq max(\nu(\mathsf{WARM}),\nu(\mathsf{HUMID})).$$
Similarly, we get:
$$\mathsf{WARM}\land\mathsf{HUMID}\vDash \mathsf{WARM}$$
This is because:
$\nu(\mathsf{WARM}\land\mathsf{HUMID})=min(\nu(\mathsf{WARM}),\nu(\mathsf{HUMID}))$ and $$ min(\nu(\mathsf{WARM}),\nu(\mathsf{HUMID}))\leq \nu(\mathsf{WARM}).$$
We also get inference patterns like the double negation law: $$\neg\neg A\vDash A\text{ and }A\vDash \neg\neg A$$ since $1-(1-x)=x$.
But other familiar reasoning patterns fail! For example, our common example of disjunctive syllogism fails:
$$\neg\mathsf{WARM},\mathsf{WARM}\lor \mathsf{HUMID}\nvDash \mathsf{HUMID}$$
To see this, take the following values:
- $\nu(\mathsf{WARM})=0.5$
- $\nu(\mathsf{HUMID})=0.25$
We get:
- $\nu(\neg\mathsf{WARM})=0.5$
- $\nu(\mathsf{WARM}\lor \mathsf{HUMID})=max(\nu(\mathsf{WARM}),\nu(\mathsf{HUMID}))=max(0.5,0.25)=0.5$
- So, $min(\nu(\neg\mathsf{WARM}), \nu(\mathsf{HUMID}\lor \mathsf{WARM}))=0.5\nleq \nu(\mathsf{HUMID})=0.25$
This means that fuzzy reasoning is indeed very different from classical reasoning. Unfortunately, a full description of the logical laws as well as sound and complete inference system are beyond what we can discuss in this book—things get mathematically quite involved.
At the same time, you have seen how fuzzy reasoning can be implemented and give its utility for developing efficient AI systems, this is certainly a logical tool to keep in one’s toolbox.
More?
In this chapter, we’ve only touched the surface of many-valued logics for AI. There are many different issues that require alternative approach. Paraconsistent logics, for example, handle reasoning with inconsistent information. There are many different kinds of fuzzy logics, which are all over AI applications. The point of this chapter was to show how one approaches such an issue. At this point, you should be able to study different non-classical logics independently.
Notes
-
There also exists weak Kleene logic, but it finds fewer applications that strong Kleene logic. ↩︎
-
A traditional issue that illustrates the point very clearly but goes beyond our topic is the so-called sorites paradox. ↩︎
Last edited: 16/10/2024