By: Johannes Korbmacher

Logic and AI

In this chapter, you’ll learn about what logic is and what it has to do with AI.

First, you’ll make acquaintance with some basic concepts of logical theory:

inference
validity, and
logical systems.

Then, you’ll learn about three ways in which logic is relevant for AI:

foundationally,
methodologically, and
instrumentally.

What is logic?

On the most general level, logic is the study of valid inference. To understand this definition better, let’s discuss inferences and validity in turn.

Inference

The basic concept of logic is that of an inference,¹ a simple piece of reasoning like the following:

Given that Ada is either on the Philosopher’s Walk or in the study, and she’s not in the study, she therefore must be on the Philosopher’s Walk.
If Alan can’t crack the code, then nobody else can. Alan can crack the code. So nobody else can.
Blondie24 is a neural network-based AI system that struggled to reach world-class checkers performance. Deep Blue, instead, is a logic-based AI system that beat the world champion in chess. This shows that logic-based AI systems are inherently better than neural network-based systems at games.
Since Watson is a logic-based AI system that beat Jeopardy!, we can conclude that some logic-based AI systems are capable of beating game shows.
GPT-4 improved upon GPT-3, which improved upon GPT-2, which, in turn, improved upon GPT-1 in terms of coherence and relevance. Therefore, the next generation of GPT models will further improve in this respect.

Before we go ahead and look more closely at the quality of these inferences, let’s introduce some important terminology.

We call phrases like “therefore”, “so”, and “we can conclude that” inference indicators.

The conclusion² of an inference is what’s being inferred or established. In 4., for example, the conclusion is that some logic-based AI systems are capable of beating game shows.

The conclusion often follows the inference indicator, but it can also be the other way around:

We know that some logic-based AI systems are capable of beating game shows, since Watson is a logic-based AI system that beat Jeopardy!.

The premises of an inference are its assumptions or hypotheses, they are what the conclusion is based on. In 4., for example, the premise is that Watson is a logic-based AI system that beat Jeopardy!

An inference can have any number of premises. While inference 4. has only one premise, inference 1. has two: that Ada is either on the Philosopher’s Walk or in the study, and that she’s not in the study. In logical theory, we also consider the limit cases of having no premises and of having infinitely many premises. More about that later.

Phrases like “given that” in 1. are called premise indicators.

Inferences are the primary subject of logical theory. Note that in logic, “inference” is a technical term, which does not necessarily have its everyday meaning. An inference is a linguistic entity, consisting of premises and a conclusion—and nothing else. It is not, for example, the psychological process of drawing a conclusion from premises.

Inferences come with the expectation that the conclusion does, in fact, follow from the premises, that the premises support the conclusion in this way. In logical terminology, we want our inferences to be valid.³ We’ll turn to what that means next.

Caveat: Our topic is not how people actually reason (psychology of reasoning), how to use arguments to convince others (rhetoric), or anything of that sort. These things are good to know, of course, but they are not our main interest.

Validity

Consider inference 1) again:

Given that Ada is either on the Philosopher’s Walk or in the study, and she’s not in the study, she therefore must be on the Philosopher’s Walk.

This looks like a pretty solid inference: if it’s indeed the case what the premises say, it must be the case what the conclusion says.

In logic, we call an inference like that, where the premises necessitate the conclusion, deductively valid. Deductive inferences are the traditional topic of most logical theory. They are often associated with mathematical reasoning.

An inference that’s not valid is called invalid. Take 2.:

If Alan can’t crack the code, then nobody else can. Alan can crack the code. So nobody else can.

This inference seems pretty hopeless: obviously, other people might still be able to crack the code even if Alan did—it might just not have been very hard.

Flawed inferences like this are also called fallacies. Frequently committed fallacies often have names. This one is called “denying the antecedent.”⁴

What about 5.?

GPT-4 improved upon GPT-3 which in turn improved upon GPT-2 and GPT-1 in terms of coherence and relevance. Therefore, the next generation of GPT models will further improve in this respect.

This inference is clearly not deductively valid: it could happen that the next generation of GPT models shows serious performance regression.

But given the evidence, such a scenario is not very likely: we’ve seen GPT models consistently improve with each new generation, so why should the next generation be any different?

An inference like this, where the premises make the conclusion (more) likely is known as an inductively valid inference. Inductive inferences play an important role in the sciences. They are often associated with statistics and probability theory.

An important difference between deductive and inductive inferences is that validity for deductive validity is all or nothing, while inductive validity comes in degrees. What we mean by this is that when it comes to deductive validity, an inference is either valid or not: the premises either necessitate the conclusion or they don’t—there’s nothing in between. With inductive inferences, instead, there are more options.

Consider the following two (hypothetical) inferences, for example:

Out of 200 randomly sampled voters, around 40% support strict AI laws. Therefore, one in two members of the general voting population supports strict AI laws.
Strict AI laws have a support of around 80% in a randomly selected sample of 20.000 voters. Therefore, support for strict AI laws in the general public is around 80%.

Neither inference seems inductively invalid—assuming the sampling was done randomly and with sufficient care, in both inferences the premise would seem to support the conclusion.

But clearly, the second inference 7. is much stronger than the first one 6.: given that the sample size is orders of magnitude larger than in the first inference, the sample is likely more representative of the actual population by making different forms of selection bias less likely.

We end up with something like the following picture:

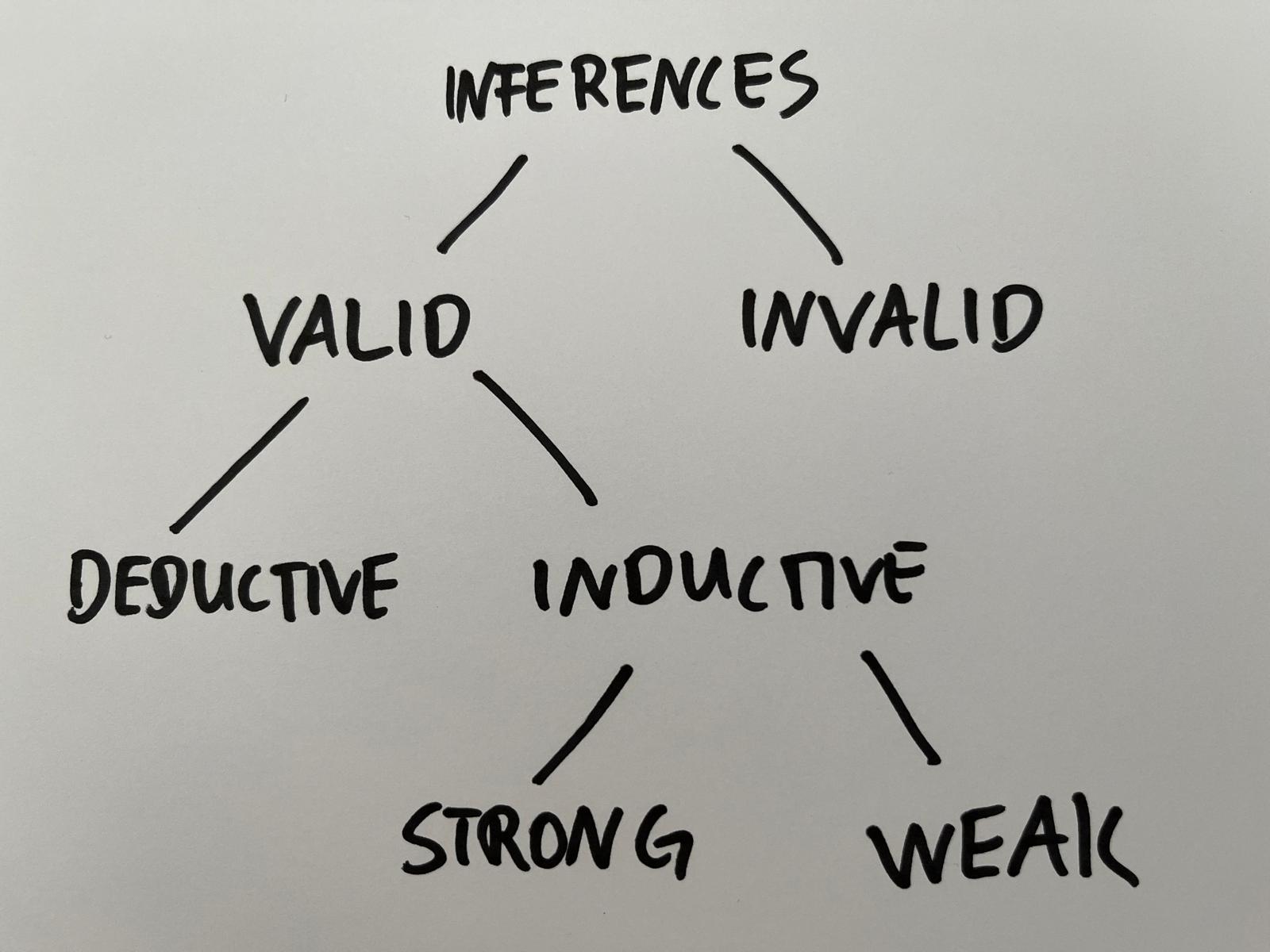
That is, on the first level, we classify inferences into valid (good) and invalid (bad) ones. Then, on the second level, we distinguish between deductively and inductively valid inferences. And finally, on the third level, we distinguish between strong and weak inductive inferences.

This concludes our overview of the subject of logical theory: logicians study the different forms of valid and invalid inference. We’ll delve further into the conceptual background of logical theory in the next chapter, where you’ll learn foundations of the concept of validity. For now, we’ll turn to the way in which logicians study this subject, we’ll look at logical systems.

Logical systems

Logicians approach the study of valid inference the way most scientists approach their subject matter: using mathematical models. We call the models that logicians use to study valid inference logical systems.

A logical system typically has three components:

a syntax, which is a model of the language of the inferences,
a semantics, which is model of the meaning of the premises and conclusions,
and a proof theory, which is a model of stepwise valid inference.

Together, these three components provide a mathematical model of valid inference. Throughout the course, you’ll learn more about syntax, semantics, and proof theory by studying how they are used in different AI applications. By the end, you’ll have a good idea of what the different components of logical systems do, and how they work together to provide a comprehensive model of valid inference.

In essence, logical systems are not all that different from the mathematical models used by physicists, for example. To illustrate, think about how a physicist would approach the question of how far our little robot SYS-2 can throw its ball:

The physicist uses Newtonian mechanics to predict how far the ball will fly, but they don’t apply the laws of mechanics directly to the real world. First, they build a mathematical model of the situation, which looks something like this:

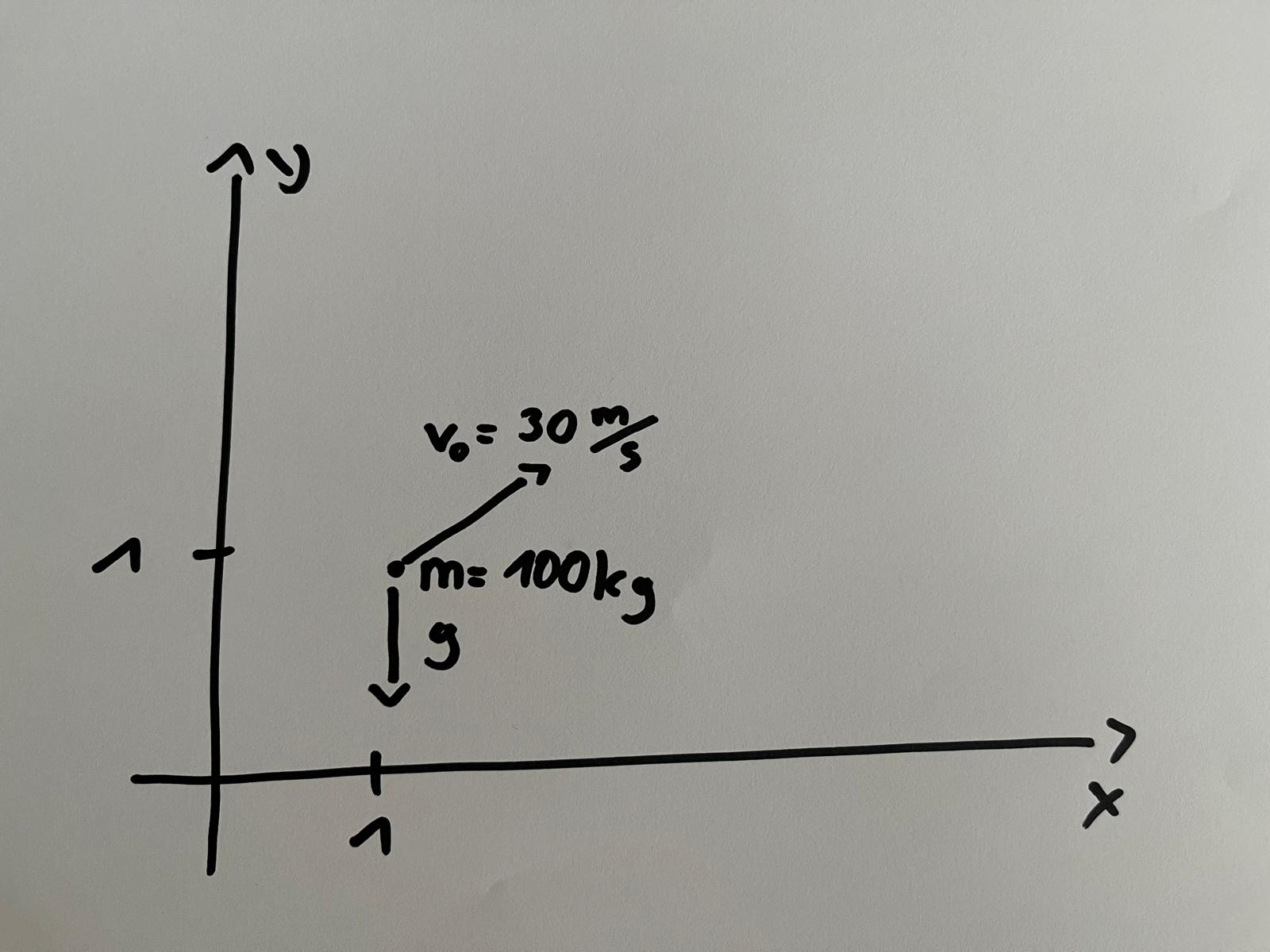
In this model, the physicist assigns a mass to the ball, represents the ball as a point in 2-dimensional Euclidian space, and treats the forces acting on the ball as vectors. Assuming that there’s no air resistance, it’s a high-school level exercise to calculate where the ball will land using the laws of classical mechanics (can you still do it?).

What’s characteristic of mathematical models is that they abstract away from irrelevant features of reality (ignoring the trees, for example), they idealize the situation (by treating the ball as a point-mass, for example), and they introduce simplifying assumptions (such as no air resistance, for example). Ultimately, this is what makes it possible to apply exact mathematical calculations to a real-world scenario like ours.

Logical systems work in just the same way as our physicist’s model: they involve abstractions, idealizations, and simplifying assumptions in order to allow us to make exact mathematical calculations about valid inference:

Syntax introduces the ideas of a formal language and of logical formulas, which are abstract representations of the logically relevant structure of premises and conclusions. This is roughly analogous to the way the physicist represents the ball as a point-mass.
Semantics introduces the idea of formal models, which are representations of meaning, spelled out in the context of formal languages. These models allow us to study logical laws, which are roughly analogous to the laws of mechanics, such as: $$F=ma$$ Interestingly, formal models often involve simplifying assumptions, such as that every sentence has a determinate truth-value from either true or false.⁵
Finally, proof theory introduces the idea of formal derivations, which are a model of stepwise valid inference. Just like the physical model calculates where the ball will land using the laws of mechanics, these derivations calculate valid inferences from the basic laws of logic.

Developing and studying logical systems is the core business of logical theory and has lead to rich body of logical knowledge, which you’ll familiarize yourself with during this course.

One last thing to note about logical systems is that there are many of them. In this course, you’ll learn about a wide range of logical systems and how they are used in AI. So, be prepared for a logical diversity!

There are different ways of classifying logical systems, but let’s just just look at two to get the point of logical diversity across.

One natural way of classifying logical systems is by the kind of inferences they deal with. For example, there are systems that deal with:

grammatical conjunctions, viz. propositional logic,
quantifiers, viz. predicate logic,
modals, viz. modal logic.

Another way of classifying logical systems is by their background assumptions/philosophies. For example, there’s:

classical logic, which assumes (among other things) that every sentence is either true or false,
intuitionistic logic, which assumes that truth needs to be “constructed”,
paracomplete and paraconsistent logics, which allow for exceptions to certain classical logical laws, such as that there’s no true contradiction.

As you’ll see different systems are useful in different contexts.

Logic in AI

Now you have a first idea of what the science of logic is all about.⁶ But before we can talk about the role of logic in AI, we need a working definition of AI.

In this course, we take AI to be the study of the models and replication of intelligent behavior. Here we’re understand “intelligent behavior” in a rather inclusive way, counting such diverse activities as behavior of switching circuits, spam filters, and self-driving cars as intelligent behavior.

There are at least three ways, in which logic is relevant to AI understood in this way. We’ll go through them in turn.

As a foundation

The first way in which logic is relevant to AI is the most direct one: valid inference simply is paradigmatic intelligent behavior. So, logical systems directly target what we’re trying to model in AI—logical systems are models of intelligent behavior. So, by our definition, logical systems are part of AI. This makes logic a subdiscipline of AI.

The relevance of logic in this sense is primarily foundational, meaning that logic contributes to the understanding of (one of) the basic concepts of AI. A part of logical theory that’s particularly relevant here is metalogic, which deals with the limits and possibilities of logical systems in principle.

Here are two famous metalogical results that (some) people think are highly relevant to AI research:

Gödel’s (first) incompleteness theorem, which implies that for every logical system that is free of internal contradictions and models basic mathematical reasoning, there is a mathematical statement that is undecidable in the system, meaning that the statement can neither be proven nor refuted in that system.

Many researchers, including Gödel himself, have thought that this has deep implications for AI. The arguments here are rather subtle and without going into the very technical details of Gödel’s result it is very easy to make mistakes, but a very rough version of the argument runs as follows:

Since the human mind is consistent and capable of mathematical reasoning, but there is no in principle undecidable mathematical fact for the human mind, Gödel’s result shows that the human mind cannot be modeled or replicated by a logical system.

If this is correct, it dooms a wide range of approaches to AI, including the logic-based approaches discussed below.
Turing’s undecidability theorem, which states that validity in the standard system of predicate logic is (algorithmically) undecidable, meaning that there is no algorithm and there can never be an algorithm that correctly determines in finitely many steps whether any given inference in the system of predicate logic is valid.

This result seems to show directly that we cannot “fully automate” validity checking using AI and maintain absolute reliability.

The relevance of logic to AI in this sense is hard to deny. At the same time, a young engineer setting out to change the world with AI, might think of logic in this sense as just theory with little practical relevance. Although logic in this sense is used for some AI applications (e.g. formal verification), it’s true that logical theory is a somewhat theoretical endeavor (which doesn’t make it any less exciting, of course 🤓). Next, we’ll turn to a much more practical relevance of logic to AI.

As a methodology

The second way in which logic is relevant to AI is that its the basis for an entire approach to AI itself, which is known as logic-based or symbolic AI. Its hard to overstate the influence that logic has had on the development of AI as a discipline: among other things, logic has influenced programming languages (LISP), the way we store knowledge (see Knowledge Representation and Reasoning or KRR for short), and advanced AI-technologies (such as WolframAlpha).⁷ It is also the approach that ultimately underpins amazing AIs such as IBM’s Watson and Deep Blue (from above). For a while, there was even the (not completely unreasonable) hope that logic could provide a complete foundation for AI, in the sense that everything you want to do in AI could be done using logical methods.

In the course, you’ll learn more about logic-based AI, but you should know right off the start that symbolic AI is no longer the predominant approach to AI. There are complex reasons for that, but its possible to get an idea why without knowing too much about logic and AI to begin with.

An good example of symbolic AI technologies are so-called expert systems, which are computer systems designed to behave like human experts at certain reasoning or decision making tasks, such as medical diagnosis or selecting computer parts for your new gaming PC.

Expert systems typically have two components: a knowledge base and an inference engine. The knowledge base (KB) stores the expert information and the inference engine derives new information from known facts using valid inference and the expert information.

The expert information typically takes the form of if-then rules. The expert information in the KB of an expert system for medical diagnosis, for example, could include the following:

If the patient has a runny nose, a sore throat, and a mild fever, then the patient likely has the common cold.

If we present the system with the known fact that our patient does have a runny nose, a sore throat, and a mild fever, the inference engine could easily derive that the patient likely has a common cold.⁸ If some symptom is missing, say the patient doesn’t have a fever, the engine can no longer validly infer that the patient has a cold—it could be something else.

This is roughly how expert systems work. By the way, this example makes it also easy to explain why expert systems (and for similar reasons other logic-based AI technologies) are also called symbolic AI: the rules and inference mechanism of an expert system are completely transparent, human-readable, and, in this sense, symbolic. Importantly, one can tell why an expert system makes a certain prediction by looking at how the inference engine arrived at the conclusion, which inference patterns it used and which pieces of expert information it relied on. This is of utmost importance for what’s known today as explainable AI or XAI for short.

To illustrate the problem with expert systems, let’s consider an ancient anecdote reported by Laërtius. According to the anecdote, Plato once defined a human as a featherless biped, much to the approval of everybody in the agora at the time (which is where the cool kids hung out). Along came history’s first punk, Diogenes, and presented Plato with a plucked chicken, remarking “Behold, Plato’s human.”

What this example shows is the following. Plato’s definition seems to give us the following if-then rule:

If something’s a featherless biped, then this is a human.

Diogenes presents us with an object that satisfies the two conditions in the if-part of the rule, but not the condition in the then-part. He found a counterexample to Plato’s definition.

The point of the anecdote, for us anyways, is that it is incredibly hard to formulate expert knowledge as if-then rules. Obviously, Plato knew how to distinguish a human from a plucked chicken, but turning this ability into an if-then clause caused even the philosophical giant to stumble. Finding correct if-then rules often requires a lot of effort, trial-and-error, etc. and then maintenance, bug-fixing, and so on. This is one of the main issues that stalled the advancement of symbolic AI—ultimately leading to the (second) AI winter and “downfall” of symbolic AI.

It turns out that statistics-based approaches, using neural networks and machine learning instead of knowledge bases and inference engines, are much more efficient at many tasks that people tried to solve using expert systems.

IBM’s Deep Blue, which beat world chess champion Gary Kasparov in the 1990s using a rule-based expert system is a success story of symbolic AI. It shows how super-human performance can be achieved using expert systems. At the same time, “beating” games like Go in the same sense eluded expert systems for a long time. It just seemed that the complexities of the game are too high to capture in a knowledge base, even after years of trying.

This changed with DeepMind’s AlphaGo, which is a neural network-based AI that’s been trained using statistical machine learning methods on large sets of game data. In a series of highly publicized events in the mid 2010s, AlphaGo managed to beat professional Go players at the highest level, suggesting the superiority of neural networks over expert systems for beating games.

Success stories like this have lead to the rise of what’s known as subsymbolic AI, which many take to be the predominant approach to AI today. Subsymbolic AI prefers conditional probabilities and inductive inference over if-then rules and deductive inference, and it prefers statistical models generated from big data over knowledge bases generated by experts. As a consequence, the information stored in a subsymbolic AI system, especially when it comes in the form of a neural network, is often opaque and hard for humans to understand.⁹ The systems seem to operate on a “lower level”, much like the neurons in the brain are on a “lower level” as compared to our thoughts and ideas—whence the name subsymbolic AI.

But if subsymbolic AI seems to dominate symbolic AI, what’s the place for logic in AI today?

As a tool

The third way in which logic is relevant to AI (partially) answers this question: logical theory provides is extremely sharp powerful tools for many different tasks in AI research and development. These tools are ultimately what the course is about.

We should note that while subsymbolic AI outperforms symbolic AI in many tasks, there are still areas where symbolic AI reigns supreme. One of these is the way we store important factual knowledge in AI systems, which is what Knowledge Representation and Reasoning (KRR) is all about.

While subsymbolic systems, especially generative AI systems like ChatGPT, can store factual information, they are—at least in the current state of the art—fairly unreliable with hallucinations being one of the main issues. If we want to have 100% recall of the stored information (think: your bank account, passwords, …), we need to use databases. Roughly, the difference between using a subsymbolic model to store information and using a symbolic model is the difference between trying to remember the information and writing it down.

The connection between databases and logic is very deep: Codd’s theorem shows that querying a database is, in many cases, essentially just a special way of evaluating the formulas of the logical system of predicate logic. KRR is just one example of where a logical tool is useful outside the scope of expert systems, and symbolic AI in the narrow sense of using logic as the sole foundation for AI. In the course, you’ll see that logical tools and methods are (almost) everywhere in AI, ranging from the way the transistors work that our computers are build from to the way neural network models “think”.

It is important to note that even subsymbolic AI systems still typically ultimately rely on inference, just statistical inductive inference and not the deductive inference that’s typically used in symbolic AI systems. In the course, we’ll pay special attention to the tight connections between logical systems and probability theory and statistics—as we’ll see they are two sides of the same coin.

Finally, there’s cutting edge research. The last years have seen the meteoric rise of generative AI systems, and especially large language models (LLMs). These are subsymbolic AI systems that are essentially large-scale probabilistic models of natural language. Under the hood, LLMs are neural networks with billions of parameters that are trained on huge sets of textual data using advanced machine-learning technologies. These neural networks approximate textual probabilities which estimate the likelihood of an expression being the next expression given a sequence of previously processed expressions.

LLMs have the impressive ability to mimic human language behavior. LLMs are the underlying technology of chatbots, like ChatGPT, who interact with humans by generating text responses to prompts—questions, instructions, descriptions, and the like. These responses are generated by repeatedly outputting the most likely next expression given the prompt and output generated so far. ChatGPT is so good at human-style interaction that it can fool you into thinking you’re talking to a human.

But despite their awesome performance on many linguistic tasks, when it comes to precise, exact reasoning, mathematical calculations, and the like, the performance of LLMs is rather poor. Many leading researchers frame the issue in terms of a distinction that’s been popularized by Daniel Kahneman in his famous popular science book Thinking, Fast and Slow.

In the book, Kahneman describes the distinction between two kinds of reasoning activities regularly performed by human agents:

System 1 thinking, which is fast, automatic, intuitive, unconscious, associative, and the like. Examples:
- recognizing a face,
- telling if one object is taller than another,
- performing simple calculations, like $5+7$,
- …
System 2 thinking, which is slow, deliberate, conscious, logical, calculating, and the like. Examples:
- counting the number of A’s in a text,
- solving a logic puzzle,
- performing complex calculations, like $432\times 441$,
- …

The diagnosis of the problem with LLMS shared promoted, e.g., by Andrej Karpathy is that LLMs are really good at system 1 thinking, but are lacking in system 2 capabilities. Symbolic systems, like expert systems, instead, are really good at system 2 thinking, but have little to no system 1 capabilities. There are different ways of tackling this problem, but one promising way that’s being explored by companies like OpenAI at the moment is to create hybrid systems, which both have symbolic and subsymbolic components. Think of teaching ChaptGPT to use calculator rather than letting it try to solve a calculation “in its head”.

This is where symbolic AI methods, especially logical methods, are once more coming to the forefront of AI research: building powerful, state-of-the-art hybrid AI systems requires a solid background in logical methods for AI—which is what you’ll acquire in this course.