By: Johannes Korbmacher

Logic and probability

In Chapters 1. Logic and AI and 2. Valid inference , we’ve distinguished between deductive inference (the truth of the premises guarantees the truth of the conclusion) and inductive inference (the truth of the premises makes the truth of the conclusion more likely). So far, we’ve only focused on models of deductive inference. In this chapter, you’ll learn more about how to model inductive inference.

We’ll begin by looking at how to model probabilities in a logical setting. We’ll then go through a useful method for calculating probabilities using probability truth-tables. After this, we turn to conditional probabilities, which then allow us to discuss a simple model of inductive validity. To conclude the chapter, we look at some examples of valid and invalid inductive inferences in our model.

Models of probability

The probability of an event describes the how likely it is that the event occurs. Think, for example, of how likely it is that you roll a 3 on a 6 sided-die, or how likely it is that it rains tomorrow.

What this really means is actually a matter of substantial debate. There different schools of thought on the interpretation of probability:

Objectivists argue that the likelihood we’re talking about here is an objective feature of reality, sometimes called objective chance. An example of this are frequentist interpretations of probability, which think of probabilities as a measure of how often an event would occur if we repeated the circumstances.
Subjectivists argue that the likelihood in question is a subjective, epistemic feature of world. An example of this are Bayesian interpretations of probability, which think of probabilities as a measure of our degree of belief in an event occurring.

Here, we won’t take sides in this debate. We’ll work with a pre-theoretic notion of probability and focus on the formalism.

Probabilities play many important roles in AI research. On the one hand, they are the basis for the statistical methods used in modern subsymbolic machine learning methods. On the other hand, probabilities are the main method for dealing with inductive inference and uncertainty in symbolic settings, such as expert systems.

Different applications of probabilities in AI use different (though equivalent) ways of developing the formalism. Here, we’ll develop a symbolic approach to probabilities, which models probabilities as real numbers assigned to formulas in formal languages.

But you should be aware of the fact that mathematical probability theory, in general, is a broader theory that can be applied in many different, symbolic and subsymbolic settings.

For now, we work ( again ) with a propositional language $\mathcal{L}$ with variables $p_1,\dots,p_n$ and connectives $\neg,\land,\lor$.

A probability for $\mathcal{L}$ is a function $Pr:\mathcal{L}\to\mathbb{R}$, which assigns real numbers to formulas, subject to the following three conditions:

$Pr(A)\geq 0$, for all $A\in\mathcal{L}$
$Pr(A)=1$, whenever $\vDash A$ (i.e. $A$ is a classical logical truth)
$Pr(A\lor B)=Pr(A)+Pr(B)$, whenever $\vDash \neg (A\land B)$ (i.e. $A\land B$ is unsatisfiable)

These are the so-called Kolmogorov axioms for classical probability theory. Note that they use notions from classical logic (logical truth and satisfiability).¹

These are only the basic axioms, there are also derived laws. For example, it’s easy to show that for all formulas $A$, we have: $$P(\neg A)=1-P(A).$$

To see this, we can reason as follows:

We know that $\vDash \neg(A\land \neg A)$ using Boolean logic.
It follows that $Pr(A\lor \neg A)=Pr(A)+Pr(\neg A)$ by the third axiom.
We further know that $\vDash A\lor \neg A$ using Boolean logic.
It follows that $Pr(A\lor \neg A)=1$ from the second axiom.
Putting it all together, it follows $1=Pr(A)+Pr(\neg A)$, which gives our claim by simple algebra (subtracting $Pr(A)$ on both sides).

In a similar way, you can show rules like the following:

$Pr(A)=0$, whenever $\vDash \neg A$
$Pr(A\lor B)=Pr(A)+Pr(B)-Pr(A\land B)$ (the “inclusion-exclusion” principle)
If $A\vDash B$, then $Pr(A)\leq Pr(B)$.
If $A$ and $B$ are equivalent, then $Pr(A)=Pr(B)$.

These kinds of laws hold for all probabilities. And importantly, there are many possible probability measures, which correspond to different modeling situations. But how do we give a concrete probability? Well, we have to give a rule that specifies the probability of every formula. Let’s look at an example.

Suppose we’re modeling the throw of a single, 6-sided die. Correspondingly, we have six propositional variables in our language: $$\mathsf{RESULT}_1,\mathsf{RESULT}_2,\mathsf{RESULT}_3,\mathsf{RESULT}_4,\mathsf{RESULT}_5,\mathsf{RESULT}_6,$$ where $\mathsf{RESULT}_i$ means that the result of the die-roll is $i$.

If we’re dealing with a fair die, we can define a corresponding probability measure $Pr_{\text{fair}}$ as follows:

$$Pr_{\text{fair}}(\mathsf{RESULT}_i)=\frac{1}{6}\text{, for }i=1,\dots,6$$ $$Pr_{\text{fair}}(\mathsf{RESULT}_i\land \mathsf{RESULT}_j)=0\text{, for all }i\neq j$$ $$Pr_{\text{fair}}(\neg\mathsf{RESULT}_1\land \dots\neg\mathsf{RESULT}_6)=0$$

The third rule ensures that we have at least one result: it’s impossible that the result isn’t $1$, isn’t $2$, $\dots$, isn’t $6$.

The second rule formalizes the fact that a die can’t show two numbers at the same time, it’s impossible that the result is both a $1$ and a $6$, say. In other words, we assume that the results are mutually exclusive.

The first rule, then, captures the fact that each result is equally likely, i.e. the die is fair. Since there are $6$ mutually exclusive results, the only way to achieve this is by assigning $\frac{1}{6}$ to each.

It turns out that these two rules are sufficient to define a value $Pr_\text{fair}(A)$ for each formula $A$. Showing this is not hard, but not trivial either.² Here we won’t go into the details, but instead highlight that probabilities are not recursive.

That is, the first rule is not sufficient to calculate the probabilities of all formulas. To calculate the probability of the die being 2 or 4, for example,

$$Pr_\text{fair}(\mathsf{RESULT}_2\lor \mathsf{RESULT}_4),$$

we need both rules:

We know from the derived inclusion-exclusion principle that: $$Pr_\text{fair}(\mathsf{RESULT}_2\lor \mathsf{RESULT}_4)=$$ $$Pr_\text{fair}(\mathsf{RESULT}_2)+Pr_\text{fair}(\mathsf{RESULT}_4)-Pr(\mathsf{RESULT}_2\land \mathsf{RESULT}_4)$$
We further know from the second rule that: $$Pr(\mathsf{RESULT}_2\land \mathsf{RESULT}_4) = 0.$$
So we get that: $$Pr_\text{fair}(\mathsf{RESULT}_2\lor \mathsf{RESULT}_4)=Pr_\text{fair}(\mathsf{RESULT}_2)+Pr_\text{fair}(\mathsf{RESULT}_4).$$
Since by the first rule, we have $Pr_\text{fair}(\mathsf{RESULT}_2)=\frac{1}{6}$ and $Pr_\text{fair}(\mathsf{RESULT}_4)=\frac{1}{6}$, we know that:

$$Pr_\text{fair}(\mathsf{RESULT}_2\lor \mathsf{RESULT}_4)=\frac{1}{6}+\frac{1}{6}=\frac{1}{3}$$

But note that crucially, we needed both rules in this calculation. The probabilities of the propositional variables are not enough, we also need the values of their conjunctions.³

In our simple example, this was easy: no conjunction could be true. But in more complex modeling scenarios, that makes specifying probabilities explicitly fairly difficult. This is why we’ll now describe a method for defining probabilities that’s easier to implement.

Probability truth-tables

It turns out that we can use truth-tables to specify probabilities for a whole language.⁴ To see how this works, let’s discuss the abstract theory first, and then go through a concrete example.

The basic idea is that we can specify probabilities by saying how likely different valuations are. Here, we think of valuations again as logically possible scenarios and of the likelihood of a valuation as how likely it is that the things in the actual world turn out exactly like in the scenario.

So, we have $\mathsf{RAIN}$ and $\mathsf{SUN}$ as our propositional variables, then we have 4 different valuations:

$\nu_1(\mathsf{RAIN})=1$ and $\nu_1(\mathsf{SUN})=1$
$\nu_2(\mathsf{RAIN})=1$ and $\nu_2(\mathsf{SUN})=0$
$\nu_3(\mathsf{RAIN})=0$ and $\nu_3(\mathsf{SUN})=1$
$\nu_4(\mathsf{RAIN})=0$ and $\nu_4(\mathsf{SUN})=0$

These correspond to the “world” where it rains and the sun shines ($\nu_1$), it rains but the sun doesn’t shine ($\nu_2$), and so forth.

We now measure with a probability weight $m$ how likely each of these scenarios is. For example, we could say:

$m(\nu_1)=0.5$
$m(\nu_2)=0.3$
$m(\nu_3)=0.2$
$m(\nu_4)=0$

What this means is that the likelihood of it raining and the sun shining is 0.5, the likelihood of it raining and the sun not shining 0.3, and so forth.

We could use any weight distribution here, as long as they sum up to $1$. This expresses the assumption that at least one of the different scenarios will happen.

So, more generally, a probability weight for our language is a function $m$, which assigns to each valuation $\nu$ a positive value $0\leq m(\nu)$ such that these values sum up to one: $$\sum_{\nu}m(\nu)=1$$

Once we have these values, we can calculate the probability of each formula by adding the probability weights of the worlds, where the formula is true: $$Pr_m(A)=\sum_{\nu(A)=1}m(\nu).$$

So, in our example, to get the probability of $\mathsf{RAIN},$ for example, we’d calculate $$Pr(\mathsf{RAIN})=\sum_{\nu(\mathsf{RAIN})=1} m(\nu)=$$ $$m(\nu_1)+m(\nu_2)=0.5+0.3=0.8$$

That is, in our model, the probability of it raining is 0.8. This is because the only scenarios where it rains are $\nu_1$ and $\nu_2$ and they have a combined likelihood of 0.8.

It turns out, as a matter of mathematical fact, that every probability function $Pr$ can be expressed in this way. We shall not look into the proof of this, but rather how to use this fact as a convenient method for specifying probabilities.

The point is that it’s much easier to specify a weight for each valuation than to assign a value to each formula: there are typically way fewer valuations than relevantly distinct formulas. Which brings us to the connection with truth-tables.

Remember from Chapter 5.2 that in a truth-table, each line corresponds to a valuation:

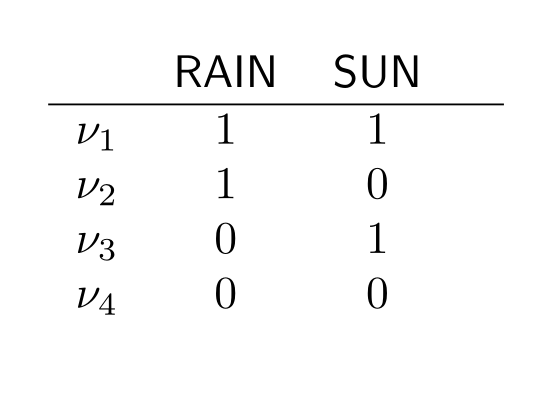
This means that in the table, we can conveniently give the information of our measure as follows:

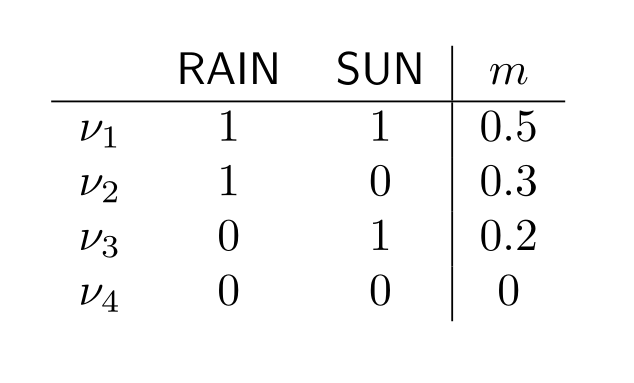
So far, so good. What makes this method really powerful is that it allows us to calculate the probability of a formula: simply calculate the values of the formula for each row in the usual way and then sum up the $m$-values for each row where the formula gets value $1$.

So, in our example, if we want to know the probability of $\mathsf{RAIN}\lor\neg\mathsf{SUN}$, we’d proceed as follows:

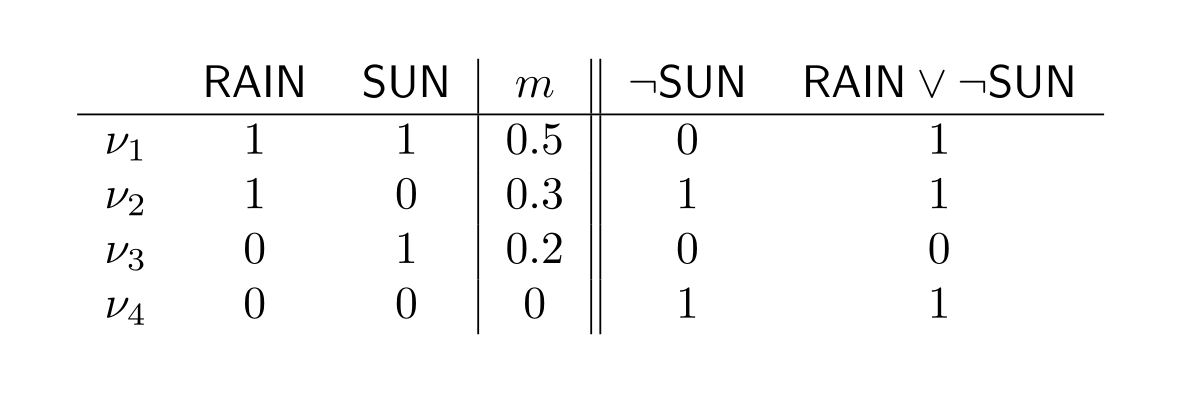
Then, we can see that: $$Pr(\mathsf{RAIN}\lor\neg\mathsf{SUN})=m(\nu_1)+m(\nu_2)+m(\nu_4)=0.5+0.3+0=0.8$$

This is a powerful method for representing and calculating probabilities. But it also has its limits. For example, it suffers from the same problem of combinatorial explosion as the truth-tables method for validity checking. For example, writing the full truth-table for our die example from above, we need $2^6=64$ rows. That means that we need to use “tricks” to handle them efficiently. In this example, we can use the fact that every row where more than one $\mathsf{RESULT}_i$ gets value $1$ will have $m$-value $0$, so we can leave it out of the table:

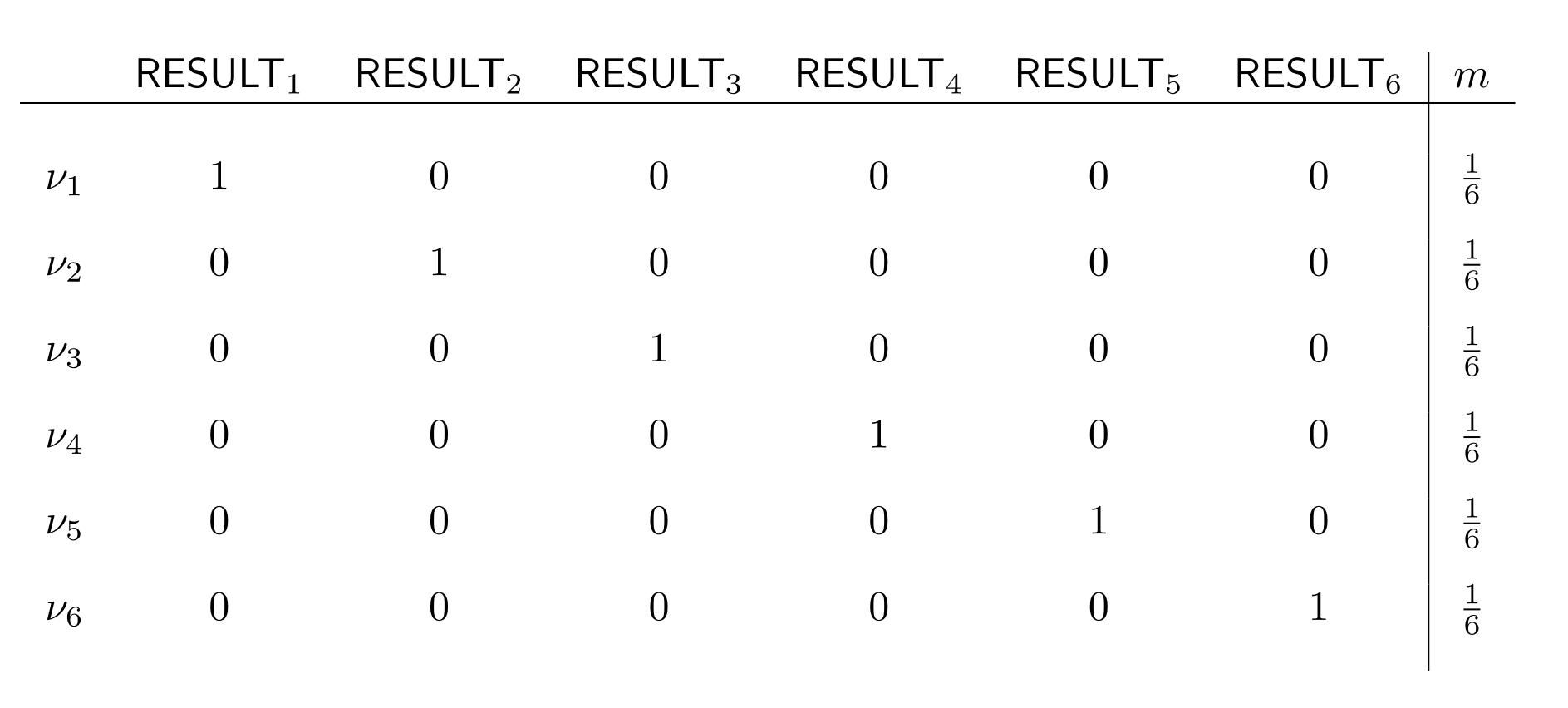
Unfortunately, computationally efficient implementations of probabilities are beyond what we can discuss in this setting.

Conditional probabilities

Having outlined what probabilities are and how we can describe them, we now turn our attention to modeling inductive inference using probabilities. As we’ve discussed already in Chapter 2. Valid inference , the idea is to use conditional probabilities for this purpose.

The conditional probability of one formula $A$ given another formula $B$ is, intuitively, a measure of how likely it is that $A$ is true assuming that $B$ is true. This idea is formally captured in the definition:

$$Pr(A\mid B)=\frac{Pr(A\land B)}{Pr(B)}$$

Here we need to assume that $Pr(B)\neq 0$ to avoid division by 0.

Let’s look at how this works in some examples:

In the $\mathsf{RAIN},\mathsf{SUN}$ example, we could ask, for example, what the probability is that it rains given that the sun is shining: $$\mathsf{Pr}(\mathsf{RAIN}\mid\mathsf{SUN})=\frac{Pr(\mathsf{SUN}\land\mathsf{RAIN})}{Pr(\mathsf{SUN})}$$

For this calculation, we need to know $Pr(\mathsf{RAIN}\land\mathsf{SUN}),Pr(\mathsf{SUN})$. We get them from the following table:

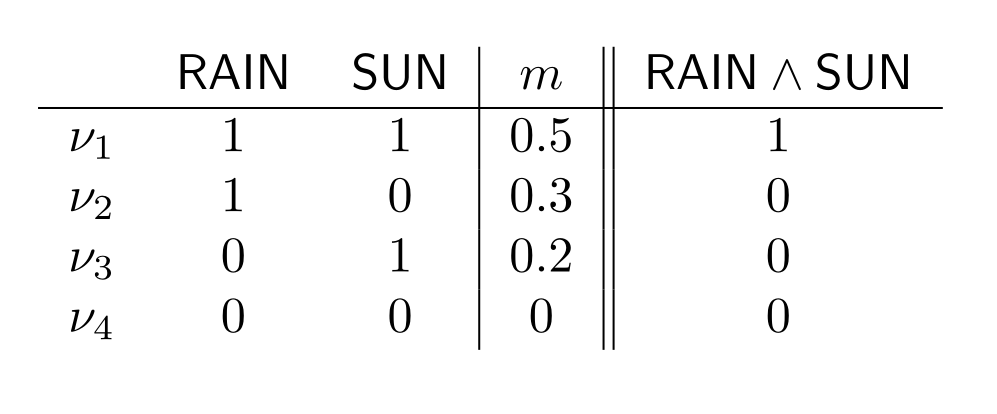
We get $Pr(\mathsf{RAIN}\land\mathsf{SUN})=0.5$ and $Pr(\mathsf{SUN})=0.5+0.2=0.7$. We get:

$$\mathsf{Pr}(\mathsf{RAIN}\mid\mathsf{SUN})=\frac{0.5}{0.7}\approx 0.71$$

So, the answer is that the chance of it raining given that the sun is shining is around 71%.
Let’s do another example to drive the point home. In our die example, let’s ask how likely it is to roll a 2 given that we roll an even number. Abbreviating $\mathsf{RESULT}_i$ to $\mathsf{R}_i$, we can represent rolling an even number with the formula $$\mathsf{R}_2\lor\mathsf{R}_4\lor\mathsf{R}_6.$$

Our question this is:

$$Pr(\mathsf{R}_2\mid \mathsf{R}_2\lor\mathsf{R}_4\lor\mathsf{R}_6 )=\frac{Pr(\mathsf{R}_2\land (\mathsf{R}_2\lor\mathsf{R}_4\lor\mathsf{R}_6))}{Pr(\mathsf{R}_2\lor\mathsf{R}_4\lor\mathsf{R}_6)}$$

We use the following simplified truth-table for the calculation:

We get:

$$Pr(\mathsf{R}_2\lor\mathsf{R}_4\lor\mathsf{R}_6)=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=\frac{1}{2}$$

$$Pr(\mathsf{R}_2\land (\mathsf{R}_2\lor\mathsf{R}_4\lor\mathsf{R}_6))=\frac{1}{6}$$

So: $$Pr(\mathsf{R}_2\mid \mathsf{R}_2\lor\mathsf{R}_4\lor\mathsf{R}_6 )=\frac{\frac{1}{6}}{\frac{1}{2}}=\frac{1}{3}$$ That is, the chance of getting a 2 given that you get an even number is $\frac{1}{3}$.

Besides helping us to define valid inductive inference, which we’ll turn to in the next section, conditional probabilities have a lot of theoretical use.

One important application that underlies many practical applications is to define the notion of probabilistic independence. We say that two formulas $A,B$ are probabilistically independent iff $$Pr(A|B)=Pr(A).$$

If $A,B$ are probabilistically independent, then whether $B$ occurs “doesn’t matter” for whether $A$ occurs.

For example, in the following example, we have that whether it rains and the sun is shining are independent:

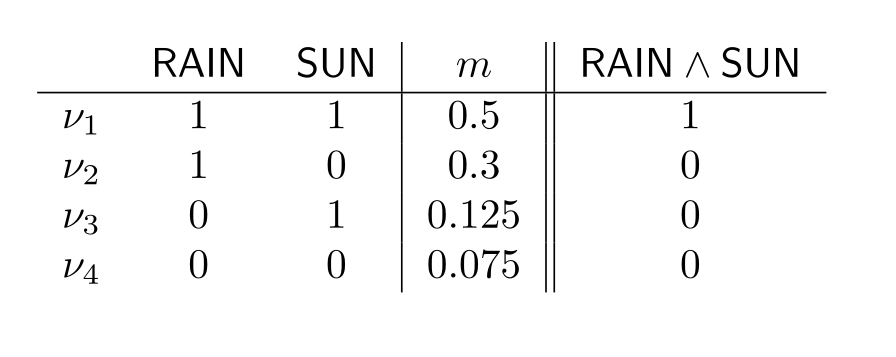
To see this, consider:

$$Pr(\mathsf{SUN}\mid \mathsf{RAIN})=\frac{Pr(\mathsf{SUN}\land\mathsf{RAIN})}{Pr(\mathsf{RAIN})}$$ $$=\frac{0.5}{0.5+0.3=0.8}=0.625=0.5+0.125=Pr(\mathsf{SUN})$$

It’s worth noting that if $A,B$ are probabilistically independent, we can calculate the probability of $A\land B$ from the probabilities of $A,B$:

If $Pr(A|B)=Pr(A)$, then $Pr(A\land B)=Pr(A)\times Pr(B)$.

This holds in our example, since $$Pr(\mathsf{RAIN})=0.5+0.3=0.8$$ $$Pr(\mathsf{SUN})=0.5+0.125=0.625$$ $$Pr(\mathsf{RAIN}\land\mathsf{SUN})=0.5=0.8\times 0.625$$

But it’s important to note that this doesn’t hold in general. In the original table:

We have:

$$Pr(\mathsf{RAIN})=0.5+0.3=0.8$$ $$Pr(\mathsf{SUN})=0.5+0.2=0.7$$ $$Pr(\mathsf{RAIN}\land\mathsf{SUN})=0.5\neq 0.8\times 0.7=0.56$$

Inductive validity

It is now time to turn to inductive validity. But before we give an account, it is important to note that inductive logic is a broad field, which is closely related to statistical inference. Given this, we should note that the account of inductive validity we present here is just one view of valid inference in a narrow sense.

The situation is similar to the one we face in deductive logic: Boolean logic, many-valued logic, fuzzy logic, etc. all give slightly different models of deductively valid inference, which are applicable in different circumstances, under different assumptions, etc.

Correspondingly, there are different models of inductive inference. The model we’ll discuss in this section is a simple version of what’s known as Bayesian inference. But we won’t go into the details of Bayesian statistics and the difference to other paradigms. Instead, we’ll focus on the idea of using conditional probability as a measure of inductive support, which is especially important in Bayesian statistics but on a general level, is characteristic of inductive inference.

The basic idea we’re pursuing is, as discussed in Chapter 2. Valid inference , the idea that an inference is inductively valid just in case the premises make the conclusion more likely. We interpret this “more likely” as: the conditional probability of the conclusion given the premises is higher than the unconditional probability of the conclusion.

Using the symbol $\mid\approx$ for inductive validity, the definition is: $$ P_1,P_2,\dots\mid\approx C \Leftrightarrow Pr(C|P_1\land P_2\land \dots)\geq Pr(C)$$ This concept is essentially what Rudolf Carnap calls the increase of firmness concept of evidential support: the premises, if we were to add them to our knowledge bank, would raise the degree with which our KB supports the conclusion.

There are a few things to note about the definition, at this point:

The right-hand side of this definition is only well-defined if $Pr(P_1\land P_2\land \dots)\neq 0$. That is, we need to assume that the premises are probabilistically consistent. What should we say if they are not? The natural answer would be that the inference should be inductively valid in the same way an inference with classically inconsistent premises is deductively valid.
The concept of inductive validity depends on a background probability. That is, technically speaking, our concept of $\mid\approx$ is relative to $Pr$ and should be written $\mid\approx_{Pr}$. In this sense, our notion of what constitutes a valid inductive inference depends on what we already know (or believe) about the world. This is an issue we’ll be revising in the next chapter, when we’ll explore logic-based learning. In practice, however, we often leave out the subscript $Pr$ and simply write $\mid\approx$.
There are, however, laws of inductive logic which don’t depend on the choice of $Pr$ and are therefore purely logical. We’ll discuss some examples below.
The notion of inductive support given by the above definition is weak. Any increase of firmness for the conclusion constitutes an inductively valid inference, not matter how small. This means that having an inductively valid inference for the conclusion from true premises is by itself not a reason to believe the conclusion.

For this, we need inductively strong inferences. These are inferences, where the conditional probability of the conclusion given the premises is high. The simplest version of this idea is where we say that: $$ P_1,P_2,\dots\mid\overset{!}{\approx} C \Leftrightarrow Pr(C|P_1\land P_2\land \dots)\gg Pr(C),$$

where $x\gg y$ means that $x$ is “much” bigger than $y$. What “much bigger” means can then depend on the context, such as, for example, what $Pr(C)$ is. An inductively strong inference may push $Pr(C)$ from $0.9$ to $0.99$ or from $0.5$ to $0.9$. What counts as a

But there are alternative notions as well: we could, for example, set a threshold $\epsilon$, typically bigger than $0.5$, for how high the probability of a conclusion needs to become in order for the inference to count as strong: $$ P_1,P_2,\dots\mid\overset{!}{\approx} C \Leftrightarrow Pr(C|P_1\land P_2\land \dots)\geq \epsilon>0.5.$$ A good inductive inference is one which makes the conclusion more likely than not.

The upshot is that in inductive logic, there is not as much uniformity as in deductive logic: different notions are available and there’s absolute agreement on what the “standard” concept should be.

We’ll continue thinking about the simple increase of firmness concept of inductive validity $\mid\approx$. We can note the following inductive laws, which are independent of the choice of $Pr$:

If $P_1,P_2,\dots\vDash C$, then $P_1,P_2,\dots\mid\approx C$.

This follows from the above observation that if $A,B$ are equivalent, then $Pr(A)=Pr(B)$. Because if $P_1,P_2,\dots\vDash C$, then, as a matter of mathematical fact we won’t show in detail, $P_1\land P_2\land\dots \land C$ is equivalent to $P_1\land P_2\land\dots$. This gives us: $$Pr(C\mid P_1,P_2,\dots)=\frac{Pr(P_1\land P_2\land \dots\land C)}{Pr(P_1\land P_2\land \dots)}=\frac{Pr(P_1\land P_2\land \dots)}{Pr(P_1\land P_2\land \dots)}=1$$

Since $1\geq Pr(C)$ for each $C$, this proves our claim.
If $C\vDash P_1\land P_2\land \dots$, then $P_1\land P_2\land \dots\mid\approx C$.

This follows from the fact that if $A\vDash B$, then $Pr(A)\leq Pr(B)$, we observed above. Because from this it follows that if $C\vDash P_1\land P_2\land \dots$, then $Pr(C)\leq Pr(P_1\land P_2\land \dots)$. Further, as before we have that $C\land P_1\land P_2\land \dots$ is equivalent to $C$ and so, we can reason as follows: $$Pr(C\mid P_1\land P_2\land \dots)=\frac{Pr(C\land P_1\land P_2\land\dots)}{Pr(P_1\land P_2\land)}$$ $$=\frac{Pr(C)}{Pr(P_1\land P_2\land\dots)}\overset{Pr(C)\leq Pr(P_1\land P_2\land \dots)}\geq Pr(C)$$

The latter law will allow us to observe the inductive validity of some well-known principles, one of which we’ll discuss on the following section.

The law is a sort of mathematical proof of the so-called deductive-nomological model of confirmation, which though not unproblematic has been hugely influential in thinking about what confirmation is.

Validities and fallacies

To conclude our theoretical discussion of inductive inference, let’s discuss two concrete examples of inductive inference, one valid, one invalid.

Enumerative induction

Enumerative induction is the principle that we can infer $\forall x P(x)$ from sufficiently many and well-chosen instances $P(a_1), P(a_2),\dots$. In our simple setting, we can express this as: $$P(a_1),P(a_2),\dots\mid\approx \forall xP(x).$$ The simple, standard example of this inference is that all observed swans, sampled well and wide, were wide, so all swans are white. Of course, this inference is deductively invalid—it can always happen that there’s a non-white swan somewhere—but we can show, mathematically, that the inference is inductively valid in the (weak) increase of firmness sense.

This follows from the previous law that if the conclusion implies the premises, an inference is inductively valid. Let’s suppose for a moment that we have extended our treatment of probabilities to a FOL language, which is rather straight-forward but takes a lot of space.⁵ Assuming that we still get our theorem (which we do), we can infer the validity of enumerative induction from the simple fact that $$\forall xP(x)\vDash P(a_i),$$ for each $i$ following the law of universal instantiation.

Even more so, given some reasonable assumptions, since the function $$Pr(\forall xP(x)\mid \dots)$$ grows monotonically, if we put every increasing numbers of instances in⁶ $$P(a_1)$$ $$P(a_1)\land P(a_2)$$ $$P(a_1)\land P(a_2)\land \dots$$ we will eventually “crack” every threshold of $\epsilon\geq 0.5$ we could chose.

This means that on our simple model of inductive validity, for sufficiently large $n$, $$P(a_1),\dots,P(a_n)\mid\overset{!}{\approx}\forall xP(x)$$

Conjunction fallacy

Here’s the original Linda problem from Tversky and Kahneman:

Linda is 31 years old, single, outspoken, and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in anti-nuclear demonstrations.

Which is more probable?

Linda is a bank teller.
Linda is a bank teller and is active in the feminist movement.

In experimental surveys, people reliably judge option 2 more likely as option 1, which is a probabilistic fallacy.

We can now see why: Since $$\mathsf{BANK}\land\mathsf{FEMINIST}\vDash \mathsf{BANK},$$ we can infer that $$Pr(\mathsf{BANK}\land\mathsf{FEMINIST})\leq Pr(\mathsf{BANK}),$$ for any $Pr$ we could chose.

There is an extensive psychological literature that tries to explain why people make this and related fallacies. But for us, from a logical perspective, the crucial point is that people do. In symbolic inductive reasoning, we have to be careful not fall into the trap of these fallacies, and the best way is to use logical methods to model inductive reasoning.