Browse course

By: Johannes Korbmacher

FOL

In this chapter, you’ll learn about first order logic (FOL), which is the benchmark for logical systems. FOL is one of the most expressive logic systems in widespread use, and it finds applications from mathematics, the sciences, to AI research.

In AI research, the main application of FOL is as a benchmark background system, in which “everything’s possible”. The impressive expressive strength of FOL allows us to formalize almost any problem we might come across, which makes FOL a great tool for knowledge engineering. At the same time, FOL has important limitations that limits its direct use for AI applications.

In this chapter, you’ll learn about the:

for FOL. After this, we’ll briefly turn to the limitations of FOL. In the next chapter, we’ll talk about the proof theory and inference strategies for FOL.

Syntax

You’ve already seen the syntax of FOL as an example in Chapter 3. Formal languages .

As quick recap, the alphabet for FOL contains:

Non-logical symbols

Both function symbols and predicates have a so-called arity, which says how many arguments they take. For example, $BiggerThan$ has arity 2, since two things stand in the relation of being bigger than: one is bigger than the other.

Logical symbols

Auxiliaries

These symbols construct formulas according to the following grammar:

$$\langle const\rangle ::= a \mid b\mid \dots $$ $$\langle var\rangle ::= x \mid y\mid \dots $$ $$\langle unop\rangle ::= \neg$$ $$\langle binop\rangle ::= \land\mid\lor\mid\to\mid\leftrightarrow$$ $$\langle quant\rangle ::= \forall\mid\exists$$ $$\langle fun^n\rangle ::= f^n\mid g^n\mid \dots $$ $$\langle term\rangle::= \langle const\rangle\mid\langle variable\rangle\mid \langle fun^n\rangle(\overbrace{\langle term\rangle,\dots,\langle term\rangle}^{n\text{ times}})$$ $$\langle pred^n\rangle ::= P^n\mid Q^n\mid \dots $$ $$\langle atom\rangle::= \langle pred^n\rangle(\underbrace{\langle term\rangle,\dots\langle term\rangle}_{n\text{ times}})$$ $$\langle fml\rangle::=\langle atom\rangle\mid\langle unop\rangle\langle fml\rangle\mid (\langle fml\rangle\langle binop\rangle \langle fml\rangle)\mid \langle quant\rangle \langle var\rangle\langle fml\rangle$$

Let’s talk for a second about what this rather complex syntax means, informally and how it can be used to express knowledge claims for the purpose of KR.

The traditional approach to natural language grammar highlights the term-predicate structure of simple sentences. A sentence like:

says of a thing, the robot, that it has a property, being smart. The sentence talks about the robot via the singular term “the robot’’ and it talks about being smart using the predicate “… is smart.''

Atomic formulas, $\langle atom\rangle$ in the grammar, model the term-predicate structure of simple sentences. Their main purpose in AI is to formalize simple pieces knowledge, like:

Using these formulas, we can directly input most basic facts into a given knowledge base.

The expressions we use to refer to objects are called terms, $\langle term\rangle$ in the formal grammar. When doing knowledge representation with FOL, we distinguish three different kinds of terms:

To each of these kinds of terms corresponds a syntactic category:

Using these kinds of expressions, we can talk about most things we might want to put information about in our knowledge base:

The crucial addition in FOL, however, are the quantifiers, they are what gives the logic its expressive strength.

In FOL we have the quantifiers $\forall$ for “for all” and $\exists$ for “there is’’ (and synonymous expressions like “every,’’ “some,’’ …).

The quantifiers allow us to formalize general knowledge claims, such as:

The variables play a crucial role in making this work. Here’s how. Take the claim that there’s a trivial knowledge base. What underlies our formalization $$\exists x(\mathsf{KB}(x)\land \mathsf{Trivial}(x))$$ is the reading:

Here “it” is an indefinite term that stands for an arbitrary but fixed object which we say exists and is a trivial knowledge base. This indefinite term is, logically speaking, a variable, which is why in our formalization “it” becomes $x$.

In many contexts, we add a distinguished identity predicate to our language $=$. Syntactically, $=$ works just like any other binary predicate: flanked by two terms it forms a formula $$t_1=t_2$$ to say that the terms $t_1,t_2$ denote the same object. When we have $=$, we often use $$t_1\neq t_2$$ to abbreviate the formula $$\neg t_1=t_2.$$

Parsing in FOL works just like in any other language. But note that the parsing tree for a formula also parses the terms involved. Here’s an example:

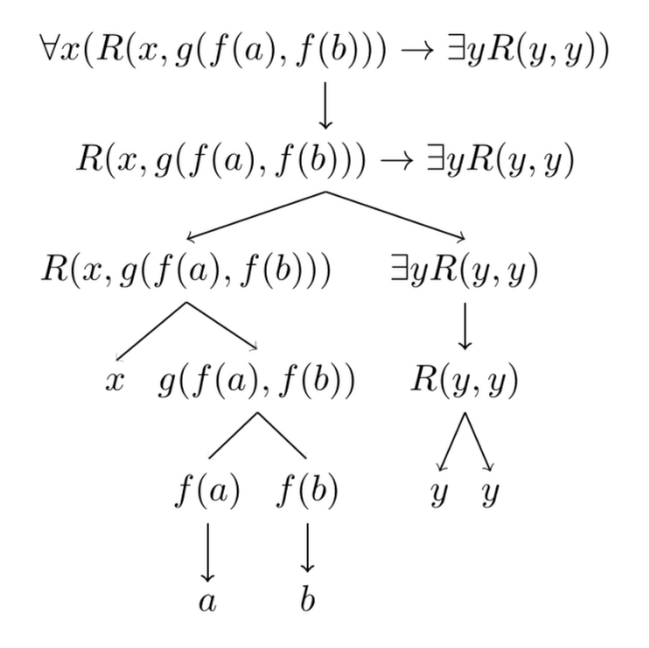
Semantics

There are different ways to interpret FOL in AI. Here, we’ll discuss the standard set-theoretic semantics. It’s the most general form of semantics for FOL, which summarizes other approaches, like database semantics or knowledge graphs.

Boolean algebra is not enough to interpret FOL. Even though Boolean truth-values and truth-function will we need more expressive structures to interpret FOL. What we need to interpret the language of FOL are the objects that our language talks about.

These object together make up the domain (of discourse). In a model for FOL, typically denoted $\mathcal{M}$, we denote the domain by $\mathcal{D}$. The domain can contain all sorts of things, but in KR-settings usually are just representations of the objects our KB talks about. In a knowledge graph, for example, we’d represent the individuals as nodes in a graph. When we’re using a database as a model for FOL, we’d use data to model the objects.

Given a domain, we need to say what our terms and predicates stand for. For the terms, that’s relatively straight-forward. For each constant, $c$, we assign a denotation from among the objects of our model: $$c^\mathcal{M}\in\mathcal{D}$$. So, we’d have, for example, a denotation $Ada^\mathcal{M}$ which is our model’s representation of Ada Lovelace. Depending on what our domain looks like, this would be a node in a graph, an entry in a database, or perhaps even a real person.

For function symbols, the denotation is simply a (mathematical) function over the domain. That means that if $f$ is an $n$-ary function symbol, then $$f^\mathcal{M}:\mathcal{D}^n\to \mathcal{D}$$ is an $n$-ary function, which takes $n$ inputs from the domain and assigns an output to them. For example, $Father^\mathcal{M}$ would be a function which assigns to the representation of each object in our model the representation of their father. We should have, for example, $$\mathsf{Father}^\mathcal{M}(Ada^\mathcal{M})=Byron^\mathcal{M}$$ In other words, the function $\mathsf{Father}^\mathcal{M}$ assigns to our representation of Ada Lovelace the representation of Lord Byron, her father.

Variables are a bit trickier to deal with. For them, we need an assignment, which tells us what they stand for. An assigment in a model with domain $\mathcal{D}$ is a function $$\alpha:\Set{x,y,z,\dots}\to\mathcal{D}$$, which says for each variable what it stands for. For example, we might have $$\alpha(x)=Ada^\mathcal{M},$$ which would mean that $x$ stands for the representation of Ada. Assignments play an important role in FOL inference, which we’ll talk about more later.

Once we’ve interpreted all our term-forming expressions over a domain, we can assign denotations to arbitrary terms using recursion: $$t^\mathcal{M}_\alpha::=\begin{cases} c^\mathcal{M} & \text{if }t=c\\ \alpha(x) & \text{if }t=x \\ f^\mathcal{M}(t_1^\mathcal{M}, \dots t_n^\mathcal{M}) & \text{if }t=f(t_1,\dots,t_n)\end{cases}$$ In this way, we get a denotation for each term $\langle term\rangle$ given a model $\mathcal{M}$ and assignment $\alpha$.

The only thing that we haven’t interpreted yet are the predicates. How does this work? Let’s look at unary predicates like $\mathsf{Red}$ first. The idea is that for each predicate $P$, we need to say which of the things in the domain $\mathcal{D}$ have the property “being $P$”. We do this directly by assigning a set $P^\mathcal{M}\subseteq \mathcal{D}$ to the predicate $P$. This set is called the extension of the predicate. In the case of $\mathsf{Red}$, for example, we’d set $\mathsf{Red}^\mathcal{M}$ to be the set of all things our model represents as red.

This generalizes to $n$-ary predicates. If we have $\mathsf{BiggerThan}$, for example, we’d assign the set $\mathsf{BiggerThan}^\mathcal{M}\subseteq\mathcal{D}\times\mathcal{D}$, which contains pairs of the form $\langle object_1,object_2\rangle$, where $object_1$ is bigger than $object_2$. Here we use the standard set-theoretic notation $\mathcal{D}^n$ to denote all the sequences of $n$ objects from the domain.

In sum, the basic concept concept of FOL semantics is that of a model, typically $\mathcal{M}$, which consists of:

Additionally, we have assignments $\alpha: \Set{x,y,z,\dots}\to\mathcal{D}$.

With all of this setup, we can re-introduce truth-values into the semantics. For FOL, our setting remains classical meaning we have the two truth-values $\Set{0,1}$ for false and true respectively.

Our aim is to assign a truth-value $\nu(A)\in\Set{0,1}$ to each FOL-formula. We do this by recursion. Once we look at how we interpreted our language, the base case is pretty clear. Take $\mathsf{Sister}(Ada,Clara)$ for example. Our model gives us:

Given this reading, we should set:

$$\nu(\mathsf{Sister}(Ada^\mathcal{M},Clara^\mathcal{M}))=1\Leftrightarrow \langle Ada^\mathcal{M},Clara^\mathcal{M}\rangle\in\mathsf{Sister}^\mathcal{M}$$

That is, in our model, the formula which says that Ada and Clara are sisters should be true just in case the pair is a member of the set of things that represent sisters.

What if variables are involved? Well, then we need assignments and our truth-value becomes relative to an assignment. So, for example, we’d have $$\nu_\alpha(\mathsf{Blue}(x))=1\Leftrightarrow \alpha(x)\in\mathsf{Blue}^\mathcal{M}$$

So, in general, then, the definition should be:

$$\nu_\alpha(P(t_1,\dots,t_n))=1\Leftrightarrow \langle (t_1)^\mathcal{M}_\alpha,\dots,(t_n)^\mathcal{M}_\alpha\rangle\in P^\mathcal{M}$$

At this point it might be important to mention that in a model, we can represent things in different ways. Of course, we should also allow models where Ada and Clara aren’t sisters, even if in reality they are.

An important exception to this is the identity predicate $=$ around. We are not allowed to freely re-interpret this predicate, it always stands for identity. That means that it’s subject to a special clause, which is:

$$\nu_\alpha(t_1=t_2)=1\Leftrightarrow t_1^\mathcal{M}=t_2^\mathcal{M}$$

Now, when it comes to the connectives $\neg,\land,\lor,\to,\dots$, we can fall back to the usual Boolean truth-functions :

$$\nu_\alpha(\neg A)=-\nu_\alpha(A)$$ $$\nu_\alpha(A\land B)=\nu_\alpha(A)\times \nu_\alpha(B)$$ $$\nu_\alpha(A\lor B)=\nu_\alpha(A)+\nu_\alpha(B)$$ $$\nu_\alpha(A\to B)=\nu_\alpha(A)\Rightarrow\nu_\alpha(B)$$

It gets interesting when it comes to the quantifiers. In addition to the Boolean truth-functions , we’ll need to find corresponding truth-functions $f_\forall,f_\exists$ for the quantifiers $\forall,\exists$.

How does this work? Let’s start with $\forall$ and take $\forall x\mathsf{Blue}(x)$, for example. What we want is to say that $\forall x\mathsf{Blue}(x)$ is true just in case all the things in our model are blue. To formally represent this, let’s introduce for each object $o\in\mathcal{D}$ an ad-hoc name $\mathbf{o}$ into our language with the stipulation that $$\mathbf{o}^\mathcal{M}=o.$$ This constant, then, allows us to consider the truth-value sequence $$\nu_\alpha(\mathsf{Blue}(\mathbf{o_1})),\nu_\alpha(\mathsf{Blue}(\mathbf{o_2})),\dots$$ for all the objects $o_1,o_2,\dots$ in the domain.

When do we want to say that $\forall x\mathsf{Blue}(x)$ is true? The answer seems to be when the sequence above just is $$1,1,1,\dots.$$ In other words, when $\nu_\alpha(\mathsf{Blue}(\mathbf{o}))=1$ for all objects $o\in\mathcal{D}$

Think about a product $$x\times y\times z\times\dots$$ where $x,y,z\in\Set{0,1}$. This number is $1$ precisely when the sequence $$x,y,z,\dots$$ is the sequence $$1,1,1,\dots.$$ This means we can give the following truth-functional analysis of the quantifiers: $$\nu_\alpha(\forall x\mathsf{Blue}(x))=\nu_\alpha(\mathsf{Blue}(\mathbf{o}_1))\times\nu_\alpha(\mathsf{Blue}(\mathbf{o}_2)\times\dots$$ where $o_1,o_2,\dots$ are all the objects in $\mathcal{D}$

We can write this in a more concise form using the mathematical notation for “long” products: $$\nu_\alpha(\forall x\mathsf{Blue}(x))=\nu_\alpha(\mathsf{Blue}(\mathbf{o}_1))\times\nu_\alpha(\mathsf{Blue}(\mathbf{o}_2))\times\dots=\prod_{o\in\mathcal{D}}\nu_\alpha(\mathsf{Blue}(\mathbf{o}))$$

Similar reasoning works for $\exists$. In order for $\nu_\alpha(\exists x\mathsf{Blue}(x))=1$, we would want to have at least one $1$ in the sequence:

$$\nu_\alpha(\mathsf{Blue}(\mathbf{o}_1)),\nu_\alpha(\mathsf{Blue}(\mathbf{o}_2)),\dots$$

We can express this using the Boolean $+$ by saying that:

$$\nu_\alpha(\exists x\mathsf{Blue}(x))=\nu_\alpha(\mathsf{Blue}(\mathbf{o}_1))+\nu_\alpha(\mathsf{Blue}(\mathbf{o}_2)+\dots$$

Mathematically, we can write this: $$\nu_\alpha(\exists x\mathsf{Blue}(x))=\nu_\alpha(\mathsf{Blue}(\mathbf{o}_1))+\nu_\alpha(\mathsf{Blue}(\mathbf{o}_2))+\dots=\sum_{o\in\mathcal{D}}\nu_\alpha(\mathsf{Blue}(\mathbf{o}))$$

The only thing left to do is to generalize this from the formulas $\forall x\mathsf{Blue}(x),\exists x\mathsf{Blue}(x)$ to arbitrary formulas of the form $\forall xA$ and $\exists xA$. For this, we just need a piece of notation: we write $\forall xA(x)$ to indicate that $A$ contains the variable $x$ that we quantify “over” and then write $A(\mathbf{o})$ for the result of replacing all the occurrences of $x$ in $A$, which are not involved in another quantifier with $\mathbf{o}$.

So, for example, if $\forall xA(x)$ is $$\forall x(\mathsf{Student}(x)\to \mathsf{OlderThan}(x,18))$$ then $$A(x)=\mathsf{Student}(x)\to \mathsf{OlderThan}(x,18))$$ and $$A(\mathbf{o})=\mathsf{Student}(\mathbf{o})\to \mathsf{OlderThan}(\mathbf{o},18)).$$

Using this notation, we can finally give the full recursive clauses for $\forall,\exists$:

$$\nu_\alpha(\forall xA(x))=\prod_{o\in\mathcal{D}}\nu_\alpha(A(\mathbf{o}))$$ $$\nu_\alpha(\exists xA(x))=\sum_{o\in\mathcal{D}}\nu_\alpha(A(\mathbf{o}))$$

This completes the rather long definition of a model for FOL, variable assignments $\alpha$, of and the associated valuation function $\nu$.

One way of looking at the aim of knowledge representation in FOL is to describe an adequate model of the way we know/think the world is like using FOL-formulas.

At this stage, we can give a definition of valid inference in FOL. We simply use the idea from Chapter 2. Valid inference of modeling deductively valid inference as truth-preservation from premises to conclusion in all models:

$$P_1,P_2,\dots \vDash C\Leftrightarrow \text{ for all }\mathcal{M},\nu,\alpha,\text{ if }\nu_\alpha(P_1)=1,\nu_\alpha(P_2)=1,\dots\text{, then }\nu_\alpha(C)=1.$$

This definition gives rise to a series of FOL laws. The following quantifier laws are especially important:

   
Duality of $\exists/\forall$ $\exists xA\vDash \neg\forall x\neg A\qquad \neg\forall x\neg A\vDash \exists xA$
Duality of $\forall/\exists$ $\forall xA\vDash \neg\exists x\neg A\qquad \neg\exists x\neg A\vDash \forall xA$
 
Distribution $\forall/\land$ $\forall x(A\land B)\vDash \forall xA\land \forall xB\qquad \forall x A\land \forall x B\vDash \forall x(A\land B)$
Distribution $\exists/\lor$ $\exists x(A\lor B)\vDash \exists xA\lor \exists xB\qquad \exists x A\lor \exists x B\vDash \exists x(A\lor B)$
 
Commutativity $\forall$ $\forall x\forall yA\vDash \forall y\forall xA$
Commutativity $\exists$ $\exists x\exists yA\vDash \exists y\exists xA$
 

There are more quantifier laws, some of which you’ll explore in the exercises.

Limitations

While Gödel’s original completeness theorem showed that the Hilbert system for FOL is sound and complete, i.e. we have $$P_1,P_2,\dots\vDash C\Leftrightarrow P_1,P_2,\dots\vdash C$$ in FOL, there are two important limiting results about FOL with severe implications for AI.

We’ve already mentioned these results in Chapter 1. Logic and AI :

These two results are explicitly about FOL. Gödel’s incompleteness theorem is concerns possible extensions of FOL axiomatizations of arithmetic, the theory of natural numbers.

While the proof of the incompleteness theorem is out of scope for this book, the result involves an impressive illustration of the expressive power of FOL:

On the other hand, Gödel’s result shows that we cannot, not matter how hard we try, develop an expert system involving a consistent knowledge bank that contains all mathematical truths. In other words, we cannot develop a consistent, mathematically omniscient AI.

Turing’s result is also about FOL. It concerns the perhaps surprising fact that while our best proof systems for FOL are sound and complete, there’s no algorithm for determining whether any given inference is valid or not. This makes inference in FOL a hard topic, which we’ll look into in the next chapter.

Just like with Gödel’s theorem, the proof of Turing’s theorem is out of scope. But what we’ll be able to appreciate are the pitfalls that naive inference algorithms in FOL can fall into, such as infinite loops in proof search, for example.

Last edited: 09/10/2024