By: Johannes Korbmacher

Boolean algebra

In this chapter, you’ll learn about some of the most fundamental laws of reasoning and computation: the laws of Boolean algebra. These laws find applications ranging from building computer circuits to web searches.

From the perspective of logical theory, Boolean algebra provides a semantics for classical propositional logic. This works by focusing on truth and falsity as the only logically relevant aspect of meaning when it comes to valid inference.

In the chapter, you will first learn about

Boolean truth-values, models, and truth-functions.

Then, we’ll use the resulting framework to define

valid inference

in semantic terms and look at the

laws

of Boolean algebra. We close with some applications.

Syntax

In this chapter, we’ll work with a simple propositional language given by the following BNF:

$$\langle prop\rangle ::= \mathsf{RAIN}\mid \mathsf{SUN} \mid \mathsf{BIKE}$$ $$\langle unop\rangle ::= \neg$$ $$\langle binop\rangle ::= \land\mid\lor$$ $$\langle fml\rangle::= \langle prop\rangle\mid \langle unop\rangle\langle fml\rangle\mid (\langle fml\rangle\langle binop\rangle \langle fml\rangle) $$

The intended interpretation of the propositional variables is:

$\mathsf{RAIN}$: it’s raining
$\mathsf{SUN}$: it’s sunny
$\mathsf{BIKE}$: I bike

Note that we left out the conditional-operators $\to$ and $\leftrightarrow$. We’ll dedicate an entire chapter to those later in the book.

Truth-values

In Boolean algebra we have two truth-values: true and false. Take $\mathsf{RAIN}$. If it is indeed raining, the truth-value of $\mathsf{RAIN}$ is true. If it is not raining, the truth-value of $\mathsf{RAIN}$ is false.

Boolean algebra further assumes that these are the only two possibilities: there is no “third” truth-value.¹ In the terminology of Chapter 1. Logic and AI , this is a modelling assumption. There are logical systems with more truth-values. Why? Well think, for example, about what the truth-value of “it’s raining tomorrow” is now. Arguably, whether it’s raining tomorrow is not decided yet, so it’s neither true nor false.

We model the two truth-values mathematical by the proverbial ones-and-zeros, where 1 stands for true and 0 for false. We denote the set of the two truth-values by: $$\mathbf{2}=\Set{0,1}.$$

A sentence has a truth-value relative to a situation. Take $\mathsf{RAIN}$ again. The sentence is true some days and false on others. Logically speaking, it’s true in some situations and false in others.

A situation in the logical sense is any way the things could turn, real or (wildly) imagined. So there’s situations where pigs fly, where the moon is made of green cheese, or where everybody loves logic-based AI.

In Boolean algebra, we model situations using valuation functions, which represent a situation in terms of the truth-values it determines for each sentence.

Models

Boolean models are functions, let’s briefly talk about what that means. A function takes one or more input arguments from one set (its domain) and to these arguments a unique output from another set (its codomain or range). Notation-wise, if the inputs of a function $f$ come from a set $X$ and the outputs from a set $Y$, we write $f:X\to Y$. If $f$ takes $n$-inputs from $X$, we write $f:X^n\to Y$.

Standard examples from math illustrate the point. Take addition $+$. This is a function that takes as input two natural numbers and spits out a single natural number, which is the sum of the two inputs. The set $\mathbb{N}$ is the set of natural numbers, so we can write: $+:\mathbb{N}^2\to \mathbb{N}$.

To denote the output of a function there are several notations. In the case of $+$, for example, the notation you’re most familiar with is this: $$2+2=4.$$ This is called infix notation, since the function goes between (“inside”) its arguments. In general, prefix notation is more common in advanced logic and mathematics. There we write: $$+(2,2)=4$$ The same fact can also be denoted by: $$+:(2,2)\mapsto 4.$$ Sometimes, we even use tables to give a function, like so:

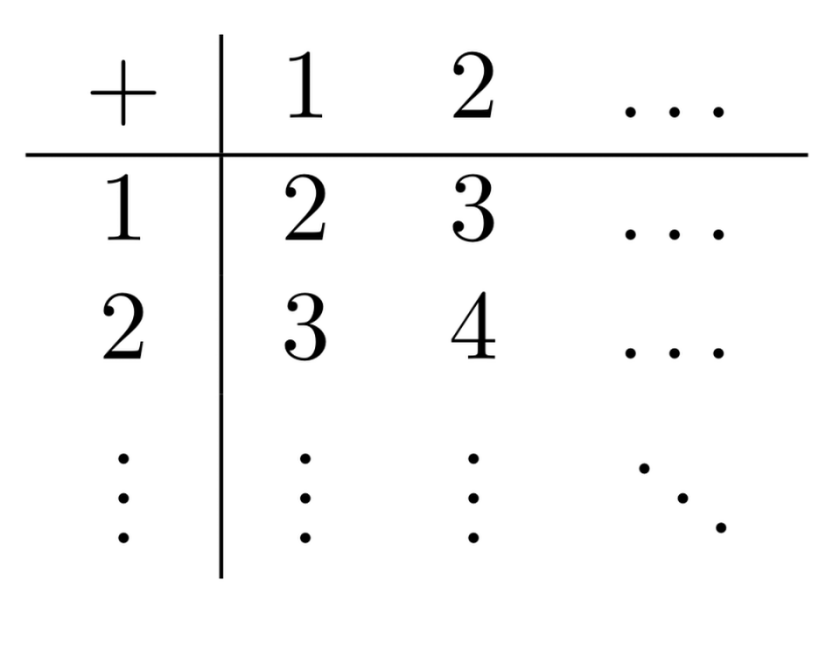
Equipped with this mathematical background, we can say that a model in Boolean algebra is a function from the set of propositional variables to the truth-values. We usually use the Greek lowercase $\nu$ (nu) to denote a given valuation function. So formally, we can define a valuation as a function $$\nu:\langle prop\rangle \to \Set{0,1}$$

But how does this model a logically possible situation? Easy!

$$\nu(\mathsf{RAIN})=1$$ means that in the situation that $\nu$ corresponds to, it is raining, $$\nu(\mathsf{RAIN})=0$$ means that it’s not.

The fact that we can use functions to model situations crucially depends on another modelling assumption, viz. that every sentence has a unique truth-value. A valuation $\nu:\langle prop\rangle \to \Set{0,1}$ will always assign a value to each of $\mathsf{RAIN},\mathsf{SUN},\mathsf{BIKE}$. E.g. $$\nu(\mathsf{RAIN})=1$$ $$\nu(\mathsf{SUN})=0$$ $$\nu(\mathsf{BIKE})=1$$ is a situation where it rains, it’s not sunny, but I’m biking.

This means that our models assume both that every sentences is either true or false and no sentence is neither true nor false. In other words, we exclude situations, where it’s, say, both raining and not raining, and we exclude situations, where it’s undecided whether it’s raining or not.

Truth-functions

At this point, we have a model of basic truth-values in situations. Each situation will provide a truth-value to each propositional variable. But what about complex formulas, like $$\neg \mathsf{RAIN}\lor\mathsf{BIKE}?$$

This is where truth-functions come into play. These are functions that take truth-values as input and give truth-values as output. In a sense, in Boolean algebra, the truth-functions model the meaning of the connectives like $\neg,\land,\lor$.

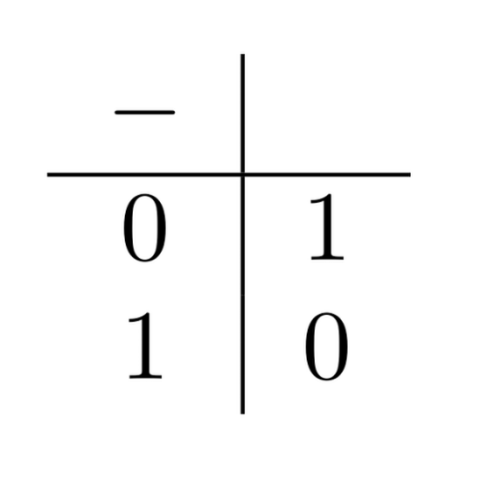
In Boolean algebra, we need 3 truth-functions, one for each connective. Their definitions are given by the following tables:

The negation function:
The conjunction function:
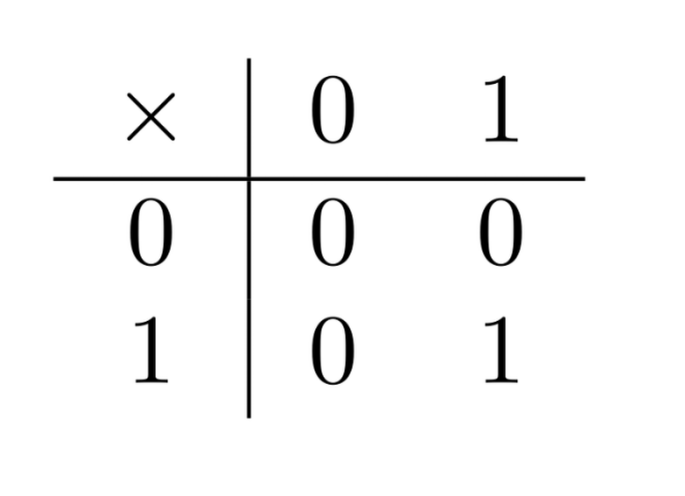
The disjunction function:

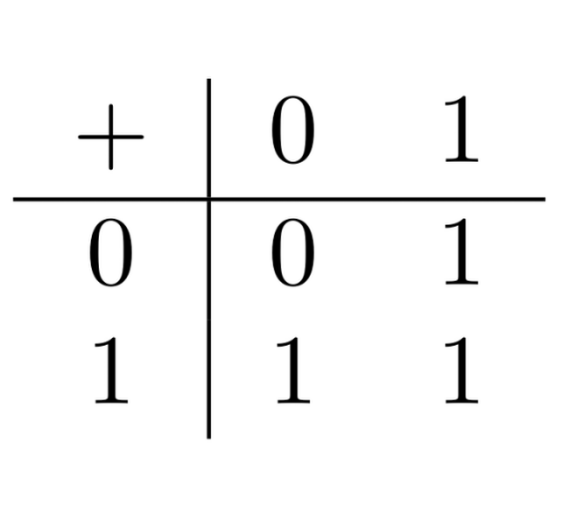
Using the truth-functions, we can calculate the truth-values for all formulas using a method known as recursion. The basic idea of recursion is that if we have a complex formula, we can calculate its truth-value from its parts using the corresponding truth-function for the operator of the formula.

So, for example, if we want to know the result of $$\nu(\mathsf{RAIN}\lor \neg\mathsf{SUNNY}),$$ we can calculate this as $$\nu(\mathsf{RAIN})+\nu(\neg\mathsf{SUNNY}).$$ So, if we know the value of $\nu(\mathsf{RAIN})$ and $\nu(\neg\mathsf{SUNNY})$. The first of the two is given by the valuation and the latter we can calculate as $-\nu(\mathsf{SUNNY})$. Suppose, for example, that $\nu(\mathsf{RAIN})=1$ and $\nu(\mathsf{SUNNY})=0$ (it’s raining and not sunny), we get that $$\nu(\mathsf{RAIN}\lor \neg\mathsf{SUNNY})=\nu(\mathsf{RAIN})+-\nu(\mathsf{SUNNY})=1+1=1.$$

The crux of recursion is that, because all propositional variables have a value and because all formulas are built up from propositional variables using the connectives, we can calculate the truth-value of every formula given a valuation. In essence: the recursive method will always “bottom out”.

In sum, if we’re given a valuation $\nu:\langle prop\rangle \to \Set{0,1}$, we can define the value $\nu(A)$ for an arbitrary formula $A$ using the following recursive rules:

$\nu(\neg A)=-\nu(A)$
$\nu(A\land B)=\nu(A)\times \nu(B)$
$\nu(A\lor B)=\nu(A)+\nu(B)$

This gives us a complete model of situations.

Validity

We’re now in a position to give a model of valid inference. In fact, we’ve basically just supplied the missing elements to fully implement the ideas from Chapter 2. Valid inference .

First, we define the semantic content $[A]$ of a formula $A$ to be $$[A]:=\Set{\nu:\nu(A)=1}.$$ Put in words, this means that the content of $A$ is the set of valuations/models, which assign to $A$ the truth-value $1$.

We then say:

$$P_1,P_2,\dots\vDash C\Leftrightarrow [P_1]\cap [P_2]\cap \dots\subseteq [C]$$

Let’s test this definition on a simple inference as a proof of concept:

Either it rains or I bike and it doesn’t rain. So, I bike.

We formalize this in our language as the claim:

$$\mathsf{RAIN}\lor \mathsf{BIKE},\neg\mathsf{RAIN}\vDash\mathsf{BIKE}$$

Let’s check out the relevant valuations:

The members of $[\mathsf{RAIN}\lor \mathsf{BIKE}]$ are:
- all valuations $\nu$ with $\nu(\mathsf{RAIN})=1$
- all valuations $\nu$ with $\nu(\mathsf{BIKE})=1$
The members of $[\neg\mathsf{RAIN}]$ are such that $\nu(\mathsf{RAIN})=0$
Since we can’t have $\nu(\mathsf{RAIN})=0$ and $\nu(\mathsf{RAIN})=1$, we know that the members of $[\mathsf{RAIN}\lor \mathsf{BIKE}]\cap [\neg\mathsf{RAIN}]$ are only the ones that $\nu(\mathsf{BIKE})=1$.
But that means that $$[\mathsf{RAIN}\lor \mathsf{BIKE}]\cap [\neg\mathsf{RAIN}]\subseteq [\mathsf{BIKE}],$$ as desired.

We have just shown mathematically that the reasoning pattern known as disjunctive syllogism is a valid inference. In similar ways, we can now test all inferences for validity.

What happens when an inference is invalid? This means that $$[P_1]\cap[P_2]\cap\dots\nsubseteq [C],$$ or, put differently, there’s a member of $[P_1],[P_2],\dots$, which is not a member of $[C]$.

Take, for example, the inference:

It rains or its sunny and it’s raining. So, it’s not sunny.

This inference is formalized as:

$$\mathsf{RAIN}\lor \mathsf{SUNNY},\mathsf{RAIN}\vDash\neg\mathsf{SUNNY}$$

It’s easy to see that this inference is invalid. Take any valuation $\nu$ with

$\nu(\mathsf{RAIN})=1$
$\nu(\mathsf{SUNNY})=1$

Remember, this is a logically possibility! ²

We then know that:

$\nu\in [\mathsf{RAIN}\lor \mathsf{SUNNY}]$
$\nu\in [\mathsf{RAIN}]$

But since $\nu(\neg\mathsf{SUNNY})=-\nu(\mathsf{SUNNY})$, we also have:

$\nu\notin [\neg\mathsf{SUNNY}]$.

We have found a countermodel.

Boolean laws

The laws of Boolean algebra are basic reasoning laws, that follow from the framework of Boolean algebra.

Using the tables, it’s easy to check the following truth-value laws for $x,y,z\in\Set{0,1}$:

Conjunction laws
Idempotence of $\times$		$x\times x=x$
Commutativity of $\times$		$x\times y=y\times x$
Associativity of $\times$		$x\times(y\times z)=(x\times y)\times z$
Identity for $\times$		$x\times 1=x$
Annihilation for $\times$		$x\times 0=0$

Disjunction laws
Idempotence of $+$		$x+x=x$
Commutativity of $+$		$x+y=y+x$
Associativity of $+$		$x+(y+z)=(x+y)+z$
Identity for $+$		$x+0=x$
Annihilation for $+$		$x+ 1=1$

Interaction laws
Distributivity $\times$ over $+$		$x\times(y+ z)=(x\times y)+(x\times z)$
Distributivity $+$ over $\times$		$x+(y\times z)=(x+ y)\times(x+ z)$
Absorption 1		$x+(x\times y)=x$
Absorption 2		$x\times(x+ y)=x$

Negation laws
Complementation 1		$x\times -x=0$
Complementation 2		$x+ -x=1$
Involution		$--x=x$
De Morgan 1		$-(x+y)=-x\times -y$
De Morgan 2		$-(x\times y)=-x+-y$

These laws are fundamental laws of thought of binary thought with wide-ranging applications.

Applications

Logical laws

From a logical perspective, the most important important application of the laws of Boolean algebra is to derive logical laws for valid inference.

Each of the laws of the previous section gives rise to a couple of corresponding laws of inference. Take the idempotence of $\times$, for example:

Let $A$ be some arbitrary formula. Consider the set

$$[A\land A]=\Set{\nu:\nu(A\land A)=1}$$

Since $\nu(A\land A)=\nu(A)\times \nu(A)$, we know by the law of idempotence for $\times$ that $\nu(A\land A)=\nu(A)$.
This means that $[A\land A]=[A]$. This means that $[A]\subseteq [A\land A]$ and that $[A\land A]\subseteq [A]$, so we can conclude that the following two inferences are valid:

$$A\vDash A\land A$$

$$A\land A\vDash A$$

Circuits

One of the most important applications of Boolean algebra is to describe the behavior of electric circuits, especially the so-called logic gates at the heart of modern computers.

To see how this works, let’s consider a simple example. At the heart of computer implementation of computation is the concept of a binary number. Essentially, binary numbers (or better binary numerals) are ways of representing natural numbers as sequences of ones-and-zeros.

The underlying ideas is that we can use the sequence $$2^0, 2^1, 2^2, 2^3,\dots$$ of exponents of $2$ to represent all natural numbers. This sequence works out to: $$1,2,4,8,\dots.$$ It’s a mathematical fact that every number can be written as a sum of numbers from this sequence.

To do so, we simply say for each number in the sequence, whether it occurs in the sum or not. For example, the sequence $$1011$$ corresponds to the number $$1\cdot 2^3+0\cdot 2^2+1\cdot 2^1+1\cdot 2^0=11.$$

An advantage of binary numbers is that they are very easy to add. Essentially, addition on binaries works component-wise:

$$\phantom{+\ }101(=5)$$ $$+\ 010(=2)$$ $$=\ 111(=7)$$

But what do we do, if we have two ones to add? Well, the answer is easy to see if we add $1$ and $1$ in binary. $1+1=2$ in the ordinary, decimal system. In binary, $2$ is written as $10$. So, you can see what we do: we carry the $1$. So, e.g.:

$$+\ 0110\ (=6)$$ $$\phantom{+\ }0101\ (=5)$$ $$=\ 1011\ (=11)$$

Now what’s astonishing from a logical perspective is that underlying this are two simple logical operations/truth-functions:

Exclusive disjunction (also known as $XOR$):

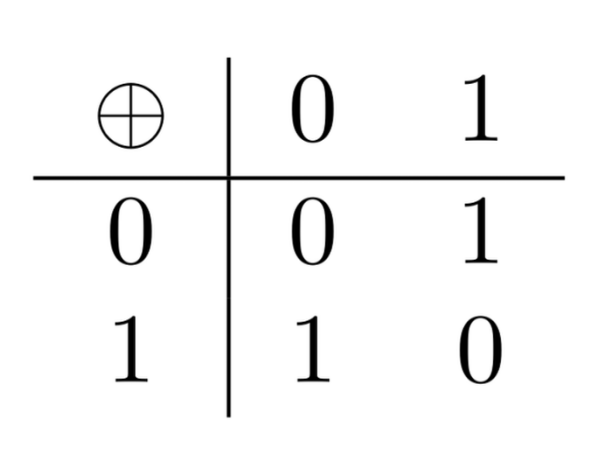
Conjunction

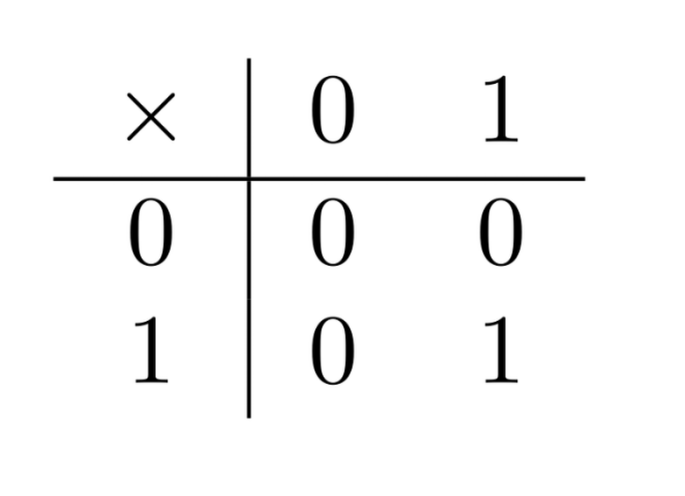
These two functions allow us to compute the result of adding two components (“bits”) of a binary number: if $x_n$ is the $n$-th component of number $x$ and $y_n$ is the $n$-th component of number $y$, then the $n$+th component of $x+y$ is: $$(x_n\oplus y_n)\oplus (x_{n-1}\times y_{n-1})$$

So, for example, for the components of $110+010$, we get:

1st component: $(0\oplus 0)\oplus (1\times 1)=1$
1st component: $(1\oplus 0)\oplus (1\times 1)=0$
2nd component: $(1\oplus 1)\oplus (0\times 0)=0$
3nd component: $(0\oplus 0)=0$

Which gives us exactly the correct result $110+010=1000$, which just means is $6+2=8$.

But this, we can express purely in terms of Boolean algebra, since we can write the function $\oplus$ as $$x\oplus y=(x+y)\times -(x\times y)$$

This has been, of course, only theory so far. But semiconductors are essentially implementations of Boolean functions and addition is indeed implemented as an optimized version of the above. This gives us a logical interpretation of addition, and shows that logic is at the heart of implementations of computation.