Valid inference

Correctness

• Valid inference = "good" inference
• Not: simple, clear, precise, ... $\Rightarrow$ rhetoric
• Validity vs fallacies:
• If it is sunny, Jan is cycling. Jan is cycling. Therefore, it is sunny.
• If it is sunny, Jan is cycling. It is sunny. Therefore, Jan is cycling.
• What's the difference?

Hypothetically

• All pigs fly. Maddy is a pig. So, Maddy flies.
• If the premises are true, then the conclusion is true.
• Possibility: Premises are false!

Definition:

An inference is valid iff the conclusion is true if (hypothetically) the premises are true

Always

• Deduction = premises guarantee conclusion
• $P_1, P_2, \dots\vDash C$
• Either it rained last night or the car is dry, the car is not dry $\vDash$ It rained last night

Mostly

• Induction = premises make likely conclusion
• $P_1, P_2, P_1, P_2, \dots\stackrel{!}{\mid\approx} C$
• 80% of 20k voters support strict laws $\stackrel{!}{\mid\approx}$ 80% of all support strict laws

Formalization

Logical form

• If it rains, the street is wet, it rains $\vDash$ The street is wet
• If it's sunny, the street is wet, it's sunny $\vDash$ The street is wet
• If pigs fly, Santa brings presents, pigs fly $\vDash$ Santa brings presents

(MP) If $A$, then $B$; $A$ $\vDash$ $B$

Propositional

• Sentences $\leadsto A, B, C, \dots$
• Not $\leadsto \neg$
• And $\leadsto \land$
• Or $\leadsto \lor$
• If ..., then ... $\leadsto~\to$

(MP) $A\to B, A\vDash B$

Quantified

• Predicates $\leadsto P(x), Q(x), R(x,y), \dots$
• Names $\leadsto a,b,c, \dots$
• All $\leadsto \forall$
• Some $\leadsto \exists$

(UI) $\forall xP(x)\vDash P(a)$

(EG) $R(a,b)\vDash \exists xR(a,x)$

Deductive logic

Features

• indefeasible
• general
• certain

Methods

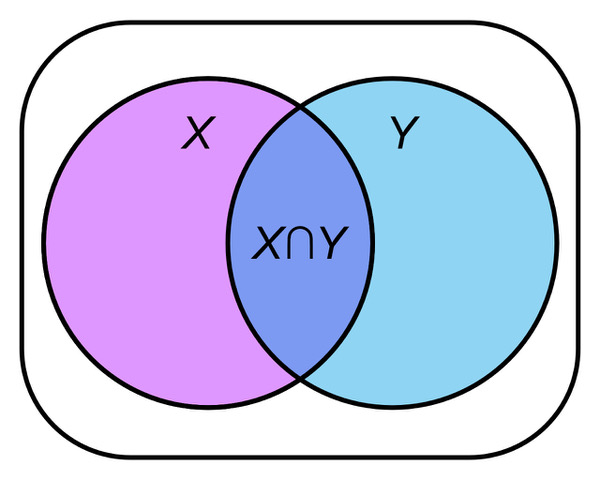
• Model = possible reasoning scenario
• $A$ is true in a model
• $[A]$ set(!) of all models
• $[A]\cap [B]$ = interesection
• $[A]\subseteq [B]$ = subset

Definition:

$P_1,P_2,\dots\vDash C$ iff $[P_1]\cap [P_2]\cap\dots\subseteq [C]$

Example

Definition:

$P_1,P_2,\dots\vDash C$ iff $[P_1]\cap [P_2]\cap\dots\subseteq [C]$

• $A\land B\vDash A$
• $[A\land B]=[A]\cap [B]$
• $[A\land B]\subseteq [A]$

Example

Definition:

$P_1,P_2,\dots\vDash C$ iff $[P_1]\cap [P_2]\cap\dots\subseteq [C]$

• $A\lor B,A\nvDash \neg B$
• $A$ true, $B$ true
• countermodel

Inductive logic

Features

• defeasible
• particular
• likely

Methods

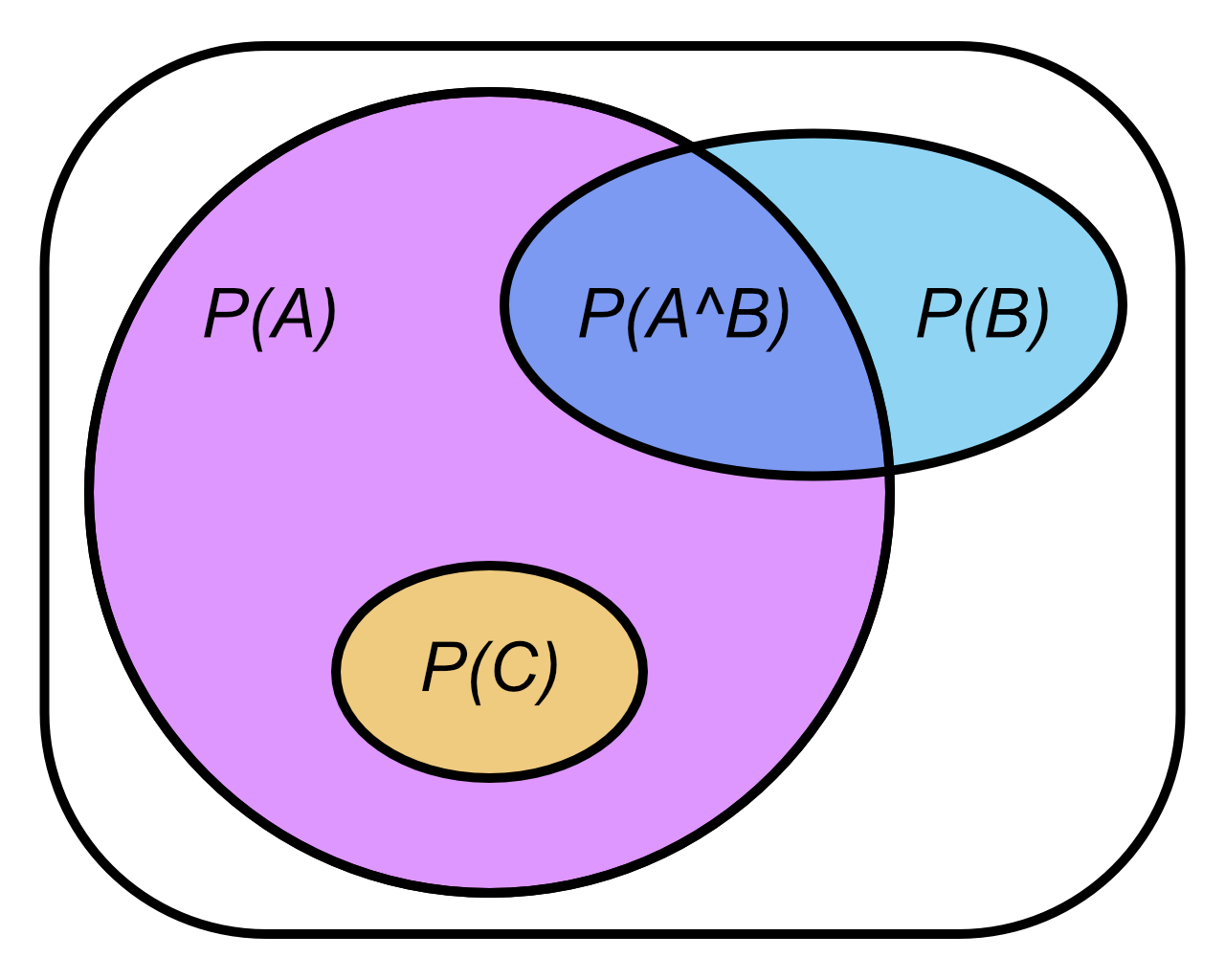
• Probability = likelihood of truth $(0,\dots,1)$
• $Pr(A)\approx$ in how many situations is $A$ true
• $Pr(A|B)\approx$ in how many situations where $B$ is true is $A$ true
• $Pr(A|B)=\frac{Pr(A\land B)}{Pr(B)}$

Definition:

$P_1,P_2,\dots\mid\approx C$ iff $Pr(C|P_1\land P_2\land \dots)>Pr(C)$

Example

Definition:

$P_1,P_2,\dots\mid\approx C$ iff $Pr(C|P_1\land P_2\land \dots)>Pr(C)$

• $A\land B\mid\approx A$
• $Pr(A|A\land B)=1$
• $Pr(A|A\land B)\geq Pr(A)$

Monotonicity

• $P_1,P_2,\dots\vDash C\Rightarrow Q,P_1,P_2,\dots\vDash C$
• $P_1,P_2,\dots\mid\approx C\nRightarrow Q,P_1,P_2,\dots\mid\approx C$
• defeasible vs indefeasible