By: Johannes Korbmacher

Formal languages

In Chapter 1. Logic and AI , we introduced formal languages as a mathematical model of language. In Chapter 2. Valid inference , we further developed the idea of formal languages as a model of logical form.

In this chapter, you’ll learn the nitty-gritty of how formal languages are defined mathematically, and we’ll look at some of the many applications of formal languages in AI and beyond.

We’ll begin by discussing:

the ideas of formal languages, and
the official definition via alphabets and grammars.

Once this definition is sufficiently clear, we’ll move to:

some examples
and the idea reading or parsing a formal language.

We conclude with some applications.

Ideas

Like much of logic, formal languages have a long history.¹ The use of abstract sentence letters as in $$A\text{ and }B$$ to express logical form can already be found in Aristotle’s Organon. Leibniz’s characteristica universalis is perhaps the first attempt at defining a formal language in the modern sense. In mathematics, the rise of formal languages is associated with rise of logical rigor in the foundations of mathematics, culminating in logicist projects, such as Gottlob Frege’s Begriffsschrift.

In logical theory, the main role of formal languages is to provide a model of logical form. Remember from Chapter 2. Valid inference that validity doesn’t depend on the concrete words or sentences involved. All of the below inferences are valid:

BERT is either my favorite dog or an LLM, and BERT not an LLM. So, BERT is my favorite dog.
Given that Ada is either on the Philosopher’s Walk or in the study, and she’s not in the study, she therefore must be on the Philosopher’s Walk.
Either Johannes or Data is teaching this class and Data is not teaching it. So, Johannes is teaching the class.

It’s easy to recognize the pattern and generate more examples of valid inferences like this. If we let $A$ and $B$ be arbitrary sentences, then the pattern is $$A\text{ or }B, \text{ not B}\vDash A.$$ This is the logical form of inferences 1.-3., which, by the way, is known as disjunctive syllogism.

From this perspective, formal languages are the result of introducing placeholders for the logically irrelevant parts of language and special symbols, so-called logical constants for the logically relevant parts of language.

In the case of disjunctive syllogism, for example, the relevant formal language will use so-called sentence letters ($p,q,r,\dots$) to stand for arbitrary sentences, and propositional connectives for the logically relevant grammatical conjunctions ($\neg$ for “not”, $\land$ for “and”, $\lor$ for “or”, $\to$ for “if …, then …”, …). We get something like this $$p\lor q,\neg p\vDash q$$ as the model for the shared logical form of inferences 1.-3. The resulting logical system, known as propositional logic, then, investigates the validity of these formal inferences.

Note that what’s happening here is very much in line with the picture from Chapter 1. Logic and AI , where we described logical systems as mathematical models of valid inference. Mathematical models, remember, are characterized by abstraction, idealization, and assumptions. Here it is easy to see, for example, where the abstraction lies: we’re abstracting away from logically irrelevant features of language, such as which concrete sentence is involved. A good example of idealization is that we’re writing a single logical constant, e.g. $\land$, for the many different ways to express conjunction in natural language: “and”, “as well as”, “together with”, …

From the perspective of logical theory, the main advantage of developing mathematical models of language and, more concretely, logical form is that it allows us to investigate valid inference with mathematical rigor, permitting us to establish (meta-)logical facts beyond any reasonable doubt. But in this course, we take a slightly more pragmatic perspective at formal languages as a logical tool.

For us, formal languages solve a fundamental problem for AI: How can we store knowledge in such a way that we can communicate it to computational models of intelligent behavior (computers)? Formal languages solve this problem because given their deterministic, mathematical nature, it is relatively easy to teach them to computers. In fact, a fundamental insight from computer science is that programming langauges are, for all intents and purposes, formal languages.

Moreover, for us as students of AI, it is important to note that database languages, which are used to create and search databases, ontology languages, which are used to create representations of factual knowledge of the world, and so on all are formal languages. In short, in knowledge representation, logical methods reign supreme.

Languages

Before we can go ahead and give the mathematical definition of what a formal language is, we need to talk a bit more about sets. Formal languages are sets. So, we need to know what a set is before we can talk about formal languages.

In 2.3.1 , you first encountered sets. We now delve a bit more into elementary set theory, the basic theory of sets.

A set is a collection of objects, called its elements or members. The elements of a set are also said to belong to the set or to be contained in the set. A set may contain any kind of objects whatsoever: numbers, symbols, people, or even other sets. For $X$ a set and $x$ an object, we write $$x\in X$$ to say that $x$ is an element of $X$ and we write $$x \notin X$$ to say that $x$ is not an element of $X$. If we have many objects $x_1, \mathellipsis, x_n$, then we also write $x_1, \mathellipsis, x_n\in X$ to say that $x_1\in X$, and …, and $x_n\in X$.

If the elements of a set are precisely $a_1, \mathellipsis, a_n$, then we can denote the set by $$\Set{a_1, \mathellipsis, a_n}.$$ This is called an extensional definition of the set. So, the set $\Set{1,a, \Set{\text{Robbie},0}}$, for example, contains precisely the number 1, the symbol $a$, and the set $\Set{\text{Robbie},0}$, which in turn contains Robbie and the number 0 as elements.

If the elements of a set are precisely the objects satisfying condition $\Phi$, then we can denote the set by $$\Set{x:\Phi(x)}.$$ This is called a definition by set abstraction. For example, $\Set{x:x\text{ is a prime number}}$ is the set that contains all and only the prime numbers. So we have that $$3\in \Set{x:x\text{ is a prime number}}$$ but $$4\notin \Set{x:x\text{ is a prime number}}.$$

Formal languages are sets of elements, which are called formulas. We usually denote formulas by uppercase letters $A,B,C,\dots$ or lowercase Greek letters $\phi,\psi,\theta,\dots$. In general, a formal language $\mathcal{L}$ is defined by two things: an alphabet, which contains the symbols the $\mathcal{L}$-formulas are built up from, and a grammar, which says how the formulas are to be constructed. Let’s discuss the two in turn.

Alphabets

Formulas are sequences of symbols, which are recruited from an alphabet. We usually write $\Sigma$ to denote the alphabet of a language.

It’s important to note that the alphabet can be any set. So, e.g.,

$$\Sigma=\Set{0,1,2,3,4,5,6,7,8,9}$$

is a perfectly fine alphabet. You can use it to define the language for all the numbers.

There is not so much more to be said about the alphabet but it’s useful to remark that in logical contexts, there are some special kinds of symbols that are usually used in the alphabets, which have special meanings.

Here is a (non-exhaustive) list. Typically, we distinguish between:

Non-logical symbols

These symbols are typically the result of logical abstraction. But in knowledge representation contexts, they can also be the result of representing extra-logical information.

Propositional variables also known as sentence letters.

These stand for sentences, like “it is raining” or “logic is awesome”. When it doesn’t matter which sentences we’re talking about, they are often $p,q,r,\dots$. In knowledge representation (KR) contexts, they can also be mnemonic, like $RAIN$ or $AWESOME$.
Constants.

These stand for proper names, like “Alan” or “Ada”. In logic, they are often $a,b,c,\dots$, but in KR-contexts, they can also be mnemonic, like $alan$ or $ada$. Sometimes, they are just ordinary numerals, like $0,1,2,\dots$ or $\pi$.
Function symbols.

These stand for functional expressions, like “+” or “the father of”. In logic, often $f,g,h,\dots$ and in KR often mnemonic, like $FatherOf$. In mathematical logic, function symbols like $+,-,\cdot, \dots$ are common, too.
Predicates.

They stand for … predicates, which are expressions that define properties or relationships, like “being blue” or “being greater than”. In logic, usually $P,Q,R,\dots$ and in KR, also mnemonics, like $BLUE$ or $GREATER$.

A special case is the identity symbol $=$, which some logicians treat as logical and some as non-logical. Otherwise, it works just like predicate.

NB: Function symbols and predicates come with an arity, which is how many arguments they take. In syntax specifications, we often write this as a superscript. So, for example, the fact that $BLUE$ applies to one thing (it’s unary) would be written $BLUE^1$.

Logical symbols

These are the result of idealization. Which logical symbols are available depends on the logical system. There symbols for many logically relevant concepts.

Variables.

These stand for arbitrary but concrete individuals or properties. They have a mainly logical function in the context of quantification, which we’ll cover more extensively later in the book.

They are typically $x,y,z,\dots$ but sometimes $\alpha,\beta,\delta$, when we’re talking about individuals. And they are typically $X,Y,Z,\dots$ when we’re talking about variables for properties.

Sentential operators.

These connect one or more sentences or phrases to form a new one. Typical examples are the classical propositional connectives:

Symbol		Meaning
$\neg,\sim$		not
$\land,\&$		and
$\lor$		or
$\to,\Rightarrow,\supset$		if …, then …
$\leftrightarrow,\Leftrightarrow,\equiv$		iff
$\vdots$		$\vdots$

But many other operators are known and/or can be introduced:

Symbol		Meaning
$\square,\lozenge$		necessity, possibility
$K,B$		knowledge, belief
$G,F,H,P$		past, future
$P,O$		permission, obligation
$!$		announcement
$?$		questions
$\vdots$		$\vdots$

Unfortunately, we won’t be able to cover most of these more advanced operators in detail.

The operators listed above are standard logical operators. But note that in programming languages, for example, we often have mnemonic conditionals, like in the following pseudocode, for example:

  IF ... THEN
      ...
  ELSE
      ...
  END IF

Similarly, programming languages often have idiosyncratic notation for the classical propositional connectives (which are, of course, easier to type on ordinary keyboards), such as $||$ for disjunction, $\&\&$ for conjunction in C, or simply $\mathsf{and}$, $\mathsf{or}$, $\mathsf{not}$ in Pyton.

Quantifiers.

These allow us to express claims about all ($\forall$) or some ($\exists$) things. More generally, quantifiers allow us to make generalizations. There are also specialized quantifiers, such as numeric quantifiers, like $\exists_3$ which says “there are exactly 3”.

Auxiliaries.

Parsing

These are symbols that help the notation of the language. They are things like commas “,” or parentheses “(” and “)”. They don’t have a meaning themselves, but they help us to disambiguate formulas. They are important for parsing (see below).

These are, in any case, only examples of some common symbols in the alphabets of formal languages. Ultimately, the sky is the limit.

The formulas, then, are sequences of symbols from the alphabet. But not every sequence of symbols is a formula, formulas are constructed from the symbols according to rules.

Grammar

The grammar of a language determines which strings of symbols from $\Sigma$ are valid expressions of the language.

In the case of most formal languages in logic, grammars use a technique known as inductive definition, which works as follows:

Our aim is to define the set $\mathcal{L}$ of (well-formed) formulas. We do this by specifying in a first step a set of atomic formulas, which are not themselves constructed. And then, in a second step, giving a set of construction rules, which tell us how to construct new formulas from old ones.

Here’s how this works for a standard language in propositional logic, where $\Sigma$ contains:

$p_1,\dots, p_n$ ($n$ propositional variables)
$\neg,\land,\lor,\to,\leftrightarrow$ (the propositional operators), and
$(,)$ (the auxiliaries).

We then say that:

$p_1,\dots, p_n \in \mathcal{L}$ and
if $A\in\mathcal{L}$, then $\neg A\in \mathcal{L}$ as well as
if $A,B\in\mathcal{L}$, then $(A\land B),(A\lor B),(A\to B),(A\leftrightarrow B)\in \mathcal{L}$

The crux of the definition is the implicit assumption that nothing else is a formula. This “closure condition” guarantees that $\mathcal{L}$ is a well-defined set, where for each sequence of symbols from $\Sigma$, we can determine whether it’s in $\mathcal{L}$ or not.

For example, we can easily see that $$(A\lor (B\leftrightarrow \neg A))$$ is a member of $\mathcal{L}$. To see this, we simply perform the construction:

We know that $A$ is a formula.
So we know that $\neg A$ is a formula.
We also know that $B$ is a formula.
So we know that $(B\leftrightarrow \neg A)$ is a formula.
So, finally, we know that $(A\lor (B\leftrightarrow \neg A))$ is a formula.

But we can also see that $\neg A\neg$ is not a formula, since no rule every allows for $\neg$ to occur in a formula without being followed by formula.

In computer science and AI, there is a wide-spread notation that significantly simplifies the above rules: the so-called Backus-Naur Form (BNF). In BNF, instead of all of the above, we can simply write:

$$A::= p_i\mid\neg A\mid (A\land A)\mid (A\lor A)\mid (A\to A)\mid (A\leftrightarrow A)$$

Here, we read the “$\mid$” as an “or”. And so this reads: a formula is either a propositional variable, or the negation of a formula, or the conjunction of two formulas, or ….

You should know that BNFs sometimes take different forms. Here is an equivalent way of giving the BNF for the same language:

$$\langle prop\rangle\mapsto p_1\mid \dots\mid p_n$$

$$\langle fml\rangle\mapsto\langle prop\rangle\mid\neg\langle fml\rangle\mid (\langle fml\rangle\land \langle fml\rangle)\mid (\langle fml\rangle\lor \langle fml\rangle)\mid $$ $$(\langle fml\rangle\to \langle fml\rangle)\mid (\langle fml\rangle\leftrightarrow \langle fml\rangle)$$

but these are just notational differences.

BNFs are a powerful method for defining formal languages. They are frequently used in logic, computer science, and AI. For example, the syntax of most programming languages is defined in BNF, see, e.g., Python. Even if you want to know what a valid email really is, you need to look up its BNF.

The formal languages we use in logic and KR are usually rather simple in that they allow for uncomplicated grammars. The complex grammatical phenomena we often encounter in natural languages, for example, which are required for to capture all linguistic nuances (which are often logically irrelevant), we need more sophisticated grammas, like context-sensitive grammars.

Examples

Here are some standard logical languages, which will frequently occur in the book:

Propositional logic

We’ve already seen the simple BNF for this:

$$A::= p_i\mid\neg A\mid (A\land A)\mid (A\lor A)\mid (A\to A)\mid (A\leftrightarrow A)$$

This works with $\Sigma=\Set{p_1,\dots,p_n,\neg,\land,\lor,\to,\leftrightarrow,(,)}$

Some remarks:

Depending on the choice of propositional variables, there are many different propositional languages. It’s always important to exactly specify what your propositional variables are.
Sometimes, we only use a subset of the operators. E.g. the language:

$$A::= p_i\mid\neg A\mid (A\land A)$$

It turns out that this language is equally expressive as the language above: everything that can be said using propositional variables and $\neg,\land,\lor,\to,\leftrightarrow$ can also be said using just $\neg,\land$. Seeing why is a topic for later in the course.
Translating natural language expressions into a formal language expression is a process known as formalization. It’s not always easy, but here are some examples for formalization with propositional languages:

The letter isn’t in the left drawer $\leadsto$ $\neg p$

It’s not the case that the letter is in the left drawer $\leadsto$ $\neg p$

The letter is in the left and in the right drawer $\leadsto$ $(p\land q)$

The letter is not in the left drawer, but it’s also not in the right one $\leadsto$ $(\neg p\land \neg q)$

The letter is in the left or in the right drawer $\leadsto$ $(p\lor q)$

The letter is neither in the left nor in the right drawer $\leadsto$ $(\neg p\land \neg q)$

If the letter is in the left drawer, then it’s not in the right drawer $\leadsto$ $(p\to \neg q)$

The letter is in the left drawer, if it’s not in the right one $\leadsto$ $(\neg q\to p)$

The letter is only in the left drawer, if it’s not in the right one $\leadsto$ $(p\to \neg q)$

The letter is in the left drawer just in case it’s not in the right one $\leadsto$ $(p\leftrightarrow \neg q)$

First-order logic

First-order logic (FOL) is extremely important in logical theory and in AI applications. In part, this is because FOL has a lot of expressive power: a lot of claims—some would say everything—can be formalized in it.

In general, the alphabet looks something like this:

$$\Set{a,b,c,\dots, x,y,z,\dots,f,g,h,\dots,P,Q,R,\dots,\neg,\land,\lor,\to,\leftrightarrow,\forall,\exists,(,),,}$$

NB: There’s no typo at the end here 😃 The last symbol is a literal comma.

For a concrete language, we’d need to pick some suitable constants $a,b,c,\dots$, function symbols $f,g,h,\dots$, and predicates $P,Q,R,\dots$. Usually, in KR-contexts, these will be mnemonic, of course.

The full syntax of FOL, then, is:

$$\langle const\rangle ::= a \mid b\mid \dots $$ $$\langle var\rangle ::= x \mid y\mid \dots $$ $$\langle unop\rangle ::= \neg$$ $$\langle binop\rangle ::= \land\mid\lor\mid\to\mid\leftrightarrow$$ $$\langle quant\rangle ::= \forall\mid\exists$$ $$\langle fu n^n\rangle ::= f^n\mid g^n\mid \dots $$ $$\langle term\rangle::= \langle const\rangle\mid\langle variable\rangle\mid \langle fun^n\rangle(\overbrace{\langle term\rangle,\dots,\langle term\rangle}^{n\text{ times}})$$ $$\langle pred^n\rangle ::= P^n\mid Q^n\mid \dots $$ $$\langle atom\rangle::= \langle pred^n\rangle(\underbrace{\langle term\rangle,\dots\langle term\rangle}_{n\text{ times}})$$ $$\langle fml\rangle::=\langle atom\rangle\mid\langle unop\rangle\langle fml\rangle\mid (\langle fml\rangle\langle binop\rangle \langle fml\rangle)\mid \langle quant\rangle \langle var\rangle\langle fml\rangle$$

As you can see, the syntax of FOL is significantly more complex than the syntax of propositional logic. But syntactically, nothing too complicated is going on. Assuming, for example, that $FRIEND$ is a binary predicate and $data$ a constant for data in our language, we can write:

$$\exists xFRIEND(data,x)$$

to say that Data has a friend.

Here are some more suggestions on how to formalize:

Not everybody handsome is smart $\leadsto$ $\neg\forall x(H(x)\to S(x))$

Everybody who’s smart is handsome $\leadsto$ $\forall x(S(x)\to H(x))$

A person who’s smart is handsome $\leadsto$ $\forall x(S(x)\to H(x))$

Someone who’s smart is handsome $\leadsto$ $\forall x(S(x)\to H(x))$

Everybody’s smart and handsome $\leadsto$ $\forall x(S(x)\land H(x))$

Somebody who’s smart exists $\leadsto$ $\exists x S(x)$

There’s somebody who’s not smart $\leadsto$ $\exists x\neg S(x)$

Somebody’s smart and somebody’s handsome $\leadsto$ $\exists xS(x)\land \exists xH(x)$

Somebody’s smart and handsome $\leadsto$ $\exists x(S(x)\land H(x))$

Nobody’s both smart and handsome $\leadsto$ $\neg\exists x(S(x)\land H(x))$

Somebody, who’s smart, is handsome $\leadsto$ $\exists x(S(x)\land H(x))$

Indeterminate terms, like pronouns, indexicals, etc., are formalized using variables. Only when clearly the same thing is meant, use the same variable, if different things could be meant, use different variables:

He’s handsome $\leadsto$ $H(x)$

She’s handsome and smart $\leadsto$ $H(x)\land S(x)$

He’s handsome and he’s smart $\leadsto$ $H(x)\land S(y)$

He’s handsome and she’s smart $\leadsto$ $H(x)\land S(y)$

That’s a smart and handsome person $\leadsto$ $H(x)\land S(x)$

Most languages used for KR are fragments of FOL, since FOL has certain theoretical limitations, which we’ll discuss later in the course.

More examples

At this point, you know enough about how logical grammars and BNFs work that you can check out your own examples. Here are some suggestions for grammars to check out:

Pick your favorite programming language (if you have one): Python we mentioned above, C is a popular low-level language, Prolog is a logic-based language.
A more complex AI example is description logic, which is a powerful KR language for designing knowledge bases.
The RFC for emails contains the BNF for valid email addresses. Check it out 🤓

Parsing

So far, we’ve looked at how to define formulas by looking at how they are constructed from simpler formulas. Now, we’ll invert the perspective and desconstruct or parse formulas.

Why? you ask? Well, the reason we need to look into this is because that’s essentially what computers do to understand formulas. The idea of parsing is to split a formula according to the rules of the grammar to recover how it was constructed.

An example shows this more clearly than words. This is the result of parsing the propositional formula $((p\land(p\to q))\to\neg q)$:

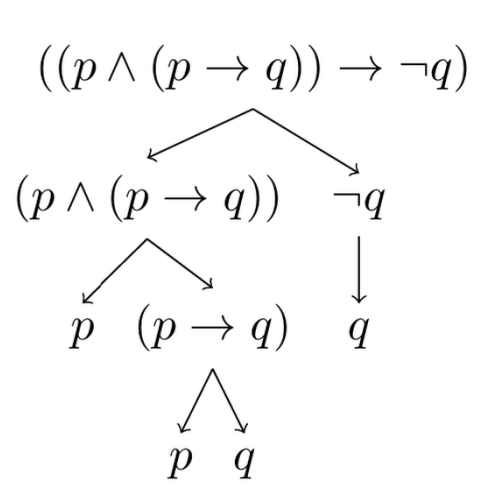
The result is what’s known as a parsing tree, it is a useful representation of the syntactic structure of a formula.

Here is an example from first-order logic:

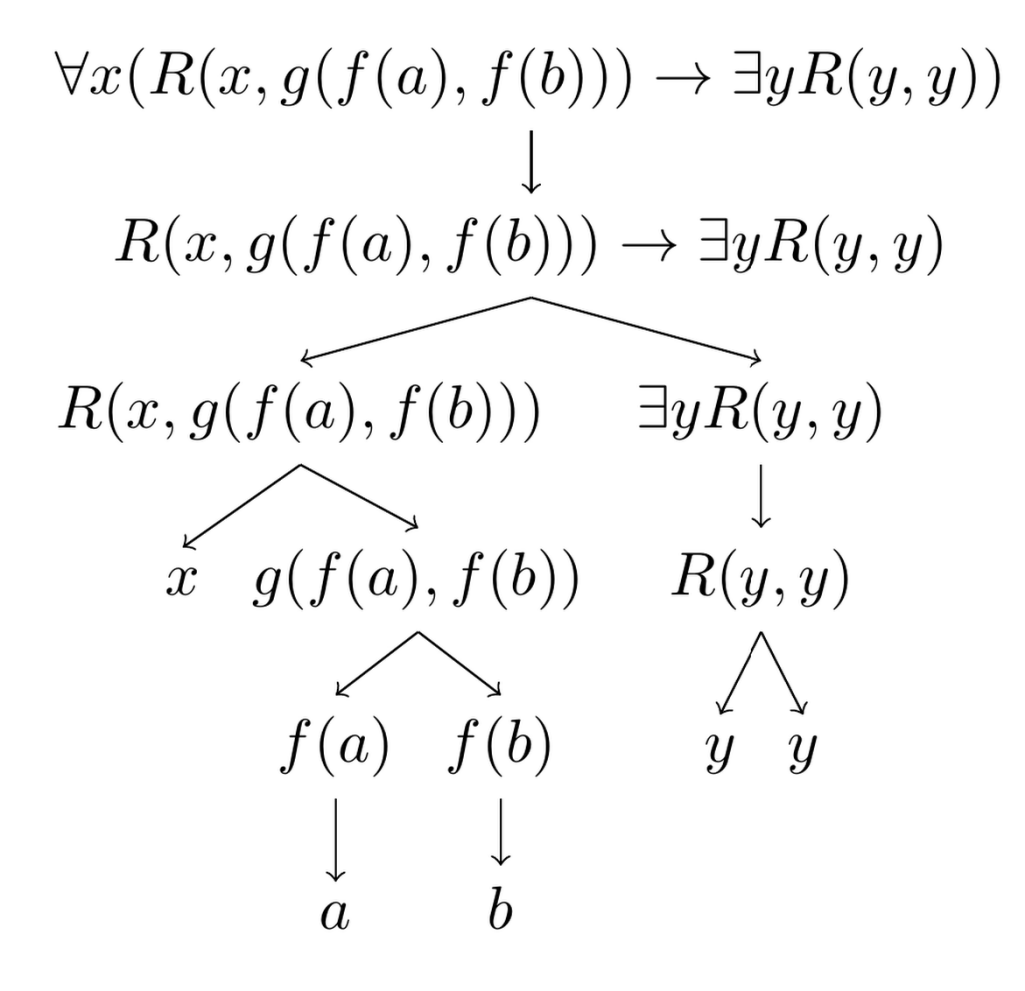
The parsing tree of a formula essentially tells you, which rules have been applied in which order to obtain the formula in question.

A fundamental insight of logical theory is that when a grammar is properly defined, we get what’s known as unique readability. Unique readability is of the utmost importance since if it fails, this means that formulas are ambiguous: they have two (or more) possible readings.

To understand the problem, consider the “formula” $p\land q\lor r$. Note that this is not really a formula because of the missing parentheses (check the rules). You could encounter this formula, for example, in a KR context, where you represent breakfast options to a computer: $p$ stands for having granola, $q$ stands for having tea, and $r$ stands for having coffee context. Now the way the “formula” is written, there are two ways of parsing it:

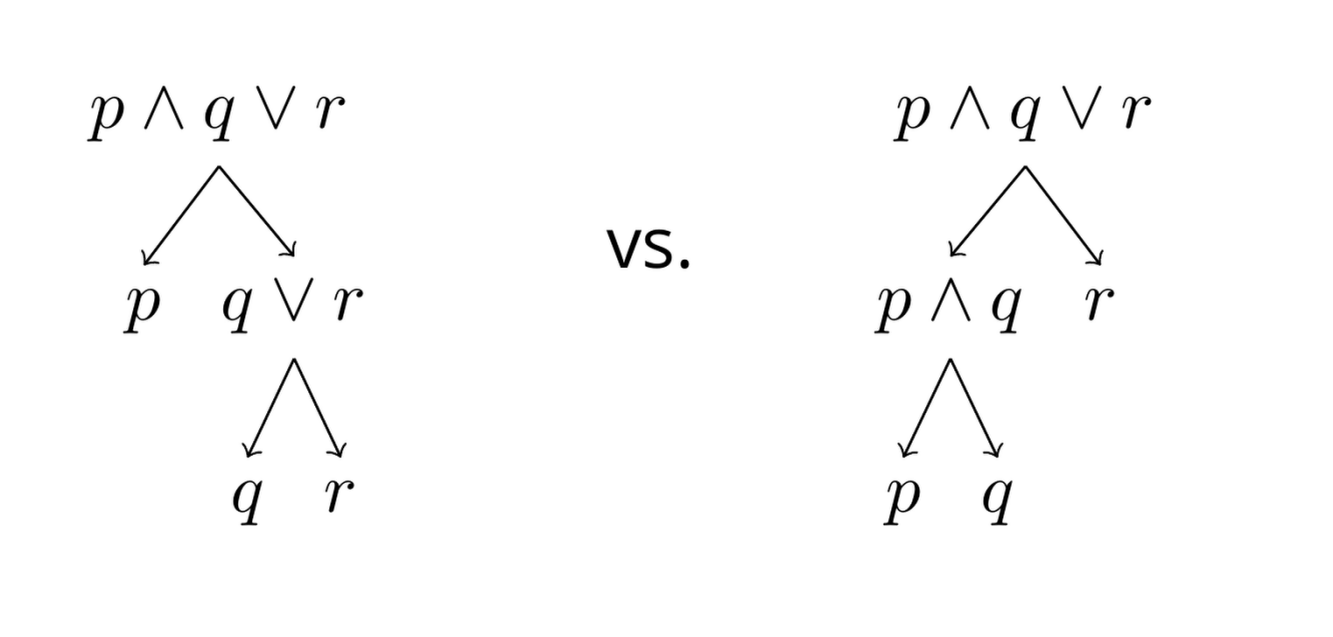
These correspond to two readings:

You can have eggs and either tea or coffee. $(p\land (q\lor r))$, the left tree
You can have eggs and tea or just coffee. $((p\land q)\lor r))$, the right tree

Obviously, these are very different things and might lead to the terrible consequence of not having anything to eat for breakfast.

This is why we need to be careful about the auxiliaries, like $(,)$, which ultimately guarantee unique readability. So, we need to be careful.

Parsing is an incredibly important subject in the foundations and practice of programming, natural language processing (NLP), and elsewhere. We don’t have time to go into the details, but think of programming for a second. A programming language is essentially a tool to write down instructions for a computer in a human-readable way. What happens “under the hood” is that the computer translates the program you write into machine instructions (the proverbial 1’s and 0’s).

To ensure that the machine instructions really correspond to what you had in mind when you wrote the program, the computer needs to understand what you meant. Since a computer is deterministic and not particularly intelligent, the only way it can do this is according to clear instructions about what means what.

But clearly, we can’t just write for each program what it means in machine instructions-otherwise, what’s the point of having the language in the first place? Instead, we specify what the individual expressions of the language mean and how combining them according to the grammar affects that meaning. In this way, we guarantee that for each program we could possibly write, we can translate it into machine instructions.

But to do so, we need to know which expressions occur in which order in the program. To determine this is the role of the parser. This shows the fundamental importance of parsing in programming and human-computer interaction.

Applications

Let’s talk for a moment about the role of formal languages in AI. We’ve already talked about the fact that programming languages are essentially just formal languages. So we can use the theory of formal languages to understand this aspect of human-machine interaction, which is crucial also in AI. Here are some other applications:

Natural language processing

One application of formula languages, parsing, and related techniques is in natural language processing (NLP). For a long time (until roughly the 1990s), formal languages played a key role in NLP in what in analogy to symbolic AI is known as symbolic NLP.

As suggested by Wikipedia, we can use a famous thought experiment known as the Chinese room to illustrate the idea:

Imagine a native English speaker who knows no Chinese locked in a room full of boxes of Chinese symbols (a data base) together with a book of instructions for manipulating the symbols (the program). Imagine that people outside the room send in other Chinese symbols which, unknown to the person in the room, are questions in Chinese (the input). And imagine that by following the instructions in the program the man in the room is able to pass out Chinese symbols which are correct answers to the questions (the output). The program enables the person in the room to pass the Turing Test for understanding Chinese but he does not understand a word of Chinese.

Jon Searle. 1999. 'The Chinese Room'

Essentially, the computer is the person in the room. The rules are parsing rules and formal grammars, which enable the room to “speak Chinese”.

The idea was to build NLP technologies in a similar way and for a while this was moderately successful. But much for the same reasons why symbolic AI in general “failedd”, symbolic NLP is no longer a strong paradigm in NLP. While symbolic methods are still around, in NLP, statistical methods, which are at the core of LLMs, for example, rule the waves.

Knowledge representation

Things are more interesting when it comes to KR. To this day, formal languages and knowledge bases (KBs) are powerful tools when it comes to storing and making accessible known facts to computational systems, such as computers or AI-systems. Mathematically speaking, a knowledge bases is just a set of formulas. In a slogan: $$\mathbf{KB}\subseteq \mathcal{L}$$

The main strengths of KBs is their reliability and precision. Mistakes in KBs are essentially only due to human error. Interestingly, though, there is ongoing research on using LLMs, for example, to store factual information, even though they can’t compete with knowledge bases yet.

What we should note, though, is that the formal languages that are used for KR are usually less expressive than FOL. This is due to some theoretical results about FOL, which provide fundamental roadblocks to using its full expressive power in computational contexts. We’ve already briefly touched upon one such reason in Chapter 1. Logic and AI , when we spoke about Turing’s undecidability theorem, which states that validity checking in FOL, specifically, cannot be fully automated. Description logic is an interesting example of an approach to KR that uses what’s effectively a fragment of FOL KR-purposes.

An active area of research is the so-called semantic web, which uses languages like OWL to make data on the internet machine readable.