By: Johannes Korbmacher

Proofs

In this chapter, you’ll learn about proof systems, an important logical tool for automated reasoning. Remember from Chapter 2. Logic and AI , that logical systems typically have three components: syntax, semantics, and proof theory. Since we’ve covered syntax in Chapter 3. Formal languages and semantics in Chapter 4. Boolean algebra , after this chapter, you’ll have seen all the components of logical systems.

First, we’ll go through the ideas, after which we’ll cover two of the most important examples of proof systems:

Hilbert systems, and
natural deduction.

Finally, you’ll learn about applications of proof systems. Specifically:

metalogic,
proof assistants,
automated theorem proving.

Ideas

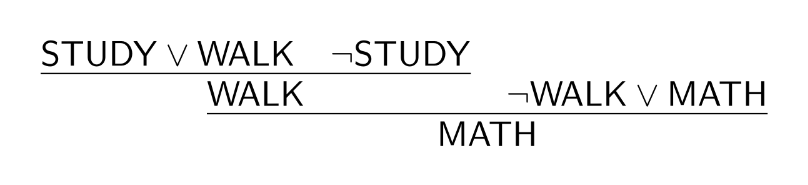
Proofs are models of step-wise inference. Think, for example, of the following inference:

Ada is either in the study or on the Philosopher’s Walk, and if she’s on the Philosopher’s Walk, she’s thinking about mathematics. Ada is not in the study, so she must be thinking about mathematics.

While the inference is deductively valid, it is rather difficult to see this immediately. It helps to split this up into a step-wise argument:

Ada is either in the study or on the Philosopher’s Walk. (Assumption)
Ada is not in the study. (Assumption)
Ada is on the Philosopher’s Walk (1.,2. via Disjunctive Syllogism)
If Ada is on the Philosopher’s Walk, then she’s thinking about mathematics. (Assumption)
Ada is thinking about mathematics. (3.,4. via Modus Ponens)

After each line, we write in parentheses a justification for the line: either it’s an assumption or something we’ve derived from other lines via a valid inference pattern. Proofs are a mathematical model of this kind of step-wise inference.

A (formal) proof is a sequence of formulas, where each formula either (i) is an assumption or known to be true or (ii) derives from the previous formulas in proof via inference rules. The final formula of a proof is the conclusion.

An inference rule is a rule that sanctions an inference from assumptions $A_1,\dots,A_n$ to a conclusion $C$. Typically, we write this in the following form:

$$\begin{array}{ccc} A_1 & \dots & A_n \\ \hline & C \end{array}$$

But there are also other notations, such as $A_1,A_2,\dots$/$C$ or $A_1,A_2,\dots\vdash C$, for example.

We write: $$A_1, A_2, \dots\vdash C$$ to say that there exists a formal proof with assumptions $A_1, A_2,\dots$ and conclusion $C$.

As we’ll see, there are many different proof systems even for just classical propositional logic. We typically clarify which system we mean by subscripting the $\vdash$ like so: $$A_1, A_2, \dots\vdash_\mathbf{S} C$$

Fully formalized, the above argument then becomes something like this:

$$\mathsf{STUDY}\lor\mathsf{WALK},\mathsf{WALK}\to\mathsf{MATH},\neg\mathsf{STUDY}\vdash\mathsf{MATH}$$

We can visually represent the corresponding proof as follows:

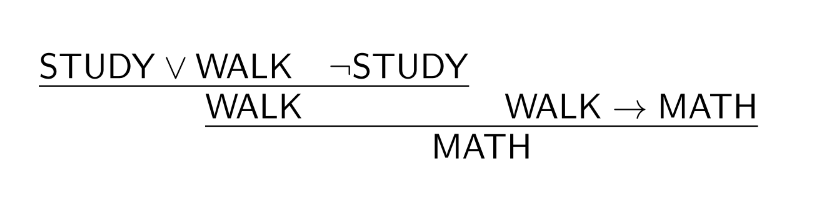
Next, we’ll go through the most important examples of different kinds of proof systems.

Proof systems

There are many different kinds of proof systems, here we’ll go through the most important examples from the perspective of logical theory.

Hilbert systems

Hilbert systems are traditionally the most common kinds of proof systems. They are modelled after mathematical axiomatic systems, where we aim to derive all relevant truths from a limited number of basic truths or axioms. All axioms are treated as known facts.

Typically, Hilbert systems have few inference rules, sometimes as few as just one.

Here’s an example of a Hilbert system for propositional logic.

All formulas of the following form are axioms:

$$ A\to ( B\to A)\tag{Axiom 1.}$$

$$( A\to ( B\to C))\to(( A\to B)\to ( A\to C))\tag{Axiom 2.}$$

$$(\neg A\to \neg B)\to ( B\to A)\tag{Axiom 3.}$$

The only inference rule is MP: $A,A\to B\vdash B$

Note that this system only uses $\to,\neg$ as its only connectives.

But there’s a “trick” to deal with the other connectives. Using the following rewriting rules, we can rewrite every formula equivalently using only $\neg$ and $\land$:

$$( A\land B)\leadsto \neg( A\to\neg B)$$ $$( A\lor B)\leadsto(\neg A\to B)$$ $$( A\leftrightarrow B)\leadsto(( A\to B)\land( B\to A))$$

This works just like the rewriting into CNF .

Here’s how derivations work in a Hilbert system. We show that $\vdash \mathsf{RAIN}\to \mathsf{RAIN}$ , i.e. we can derive the logical truth $\mathsf{RAIN}\to \mathsf{RAIN}$ (if it rains, it rains) from the axioms only:

$((\mathsf{RAIN} \to ((\mathsf{RAIN} \to \mathsf{RAIN}) \to \mathsf{RAIN})) \to ((\mathsf{RAIN} \to (\mathsf{RAIN} \to \mathsf{RAIN})) \to (\mathsf{RAIN} \to \mathsf{RAIN})))$

(Axiom 2. with $A=\mathsf{RAIN}, B=(\mathsf{RAIN}\to \mathsf{RAIN}),$ and $C=\mathsf{RAIN}$)
$(\mathsf{RAIN} \to ((\mathsf{RAIN} \to \mathsf{RAIN}) \to \mathsf{RAIN}))$

(Axiom 1. with $A=\mathsf{RAIN}$ and $B=(\mathsf{RAIN}\to \mathsf{RAIN})$)
$((\mathsf{RAIN} \to (\mathsf{RAIN} \to \mathsf{RAIN})) \to (\mathsf{RAIN} \to \mathsf{RAIN}))$

(From 1. and 2. by MP.)
$(\mathsf{RAIN} \to (\mathsf{RAIN} \to \mathsf{RAIN}))$

(Axiom 1. with $A=\mathsf{RAIN}$ and $B=\mathsf{RAIN}$.)
$(\mathsf{RAIN} \to \mathsf{RAIN})$

(From 3. and 4. by MP.)

It is far from easy to find derivations like this. It is hard to learn for both humans and machines. On the upside, Hilbert systems are economical from a mathematical perspective. They are easy to define and to investigate, making them ideal for metalogical applications.

But Hilbert systems also have practical use. They are relatively easy to apply when assumptions are involved and we translate the formulas in question using the re-writing rules mentioned above.

Let’s look at a Hilbert-style proof for: $$\mathsf{STUDY}\lor\mathsf{WALK},\mathsf{WALK}\to\mathsf{MATH},\neg\mathsf{STUDY}\vdash\mathsf{MATH}$$

First, we need to rewrite $\mathsf{STUDY}\lor\mathsf{WALK}$ using the rules to $\neg \mathsf{STUDY}\to\mathsf{WALK}$. So, what we really show is: $$\neg\mathsf{STUDY}\to\mathsf{WALK},\mathsf{WALK}\to\mathsf{MATH},\neg\mathsf{STUDY}\vdash\mathsf{MATH}$$ We get:

$\neg \mathsf{STUDY}\to\mathsf{WALK}$ (Assumption)
$\neg \mathsf{STUDY}$ (Assumption)
$\mathsf{WALK}$ (1.,2. MP)
$\mathsf{WALK}\to\mathsf{MATH}$ (Assumption)
$\mathsf{MATH}$ (3.,4. MP)

This is a pretty straight-forward derivation, just using MP twice. One way of looking at it is that the chaining algorithms we discussed in Chapter 6. Conditionals are essentially an effective way of finding Hilbert-style proofs from the knowledge base.

Natural deduction

Natural deduction systems solve the problem of being difficult to learn for humans. They are intended to mimic the actual step-by-step derivations we make “in our heads”.

Natural deduction systems have no axioms, they are entirely rule-based. The standard system for classical propositional logic, for example, looks like this:

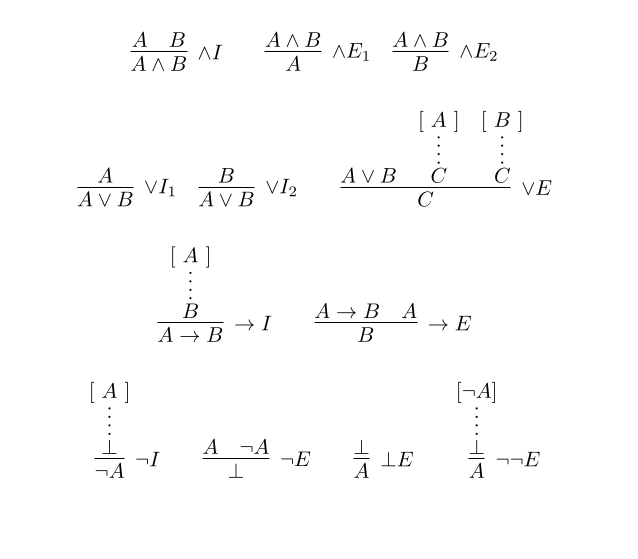
These rules need some explanation:

The symbol $\bot$ is a logical symbol that stands for a logical contradiction. It has some special rules but otherwise, it works just like any other propositional variable.

In natural deduction, you can always introduce new assumptions to your proof by simply using them in an inference rule. The crucial thing is that you can discharge assumptions, as in the rule for $\to I$:

$$\begin{array}{ccc} [A] \\ \vdots \\ B \\ \hline A\to B \end{array}$$

What this rule says is that if you have a derivation of $B$ from $A$ using the rules of natural deduction, you can treat the assumption $A$ as discharged and it no longer counts as an assumption.

This is, for example, how we would derive the logical truth $\neg(\mathsf{RAIN}\land\neg\mathsf{RAIN})$ (it’s not both raining and not raining):

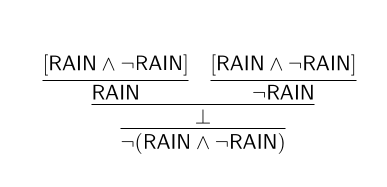
So, we get $\vdash\neg(\mathsf{RAIN}\land\neg\mathsf{RAIN})$ Note that there are no assumptions in this claim. The assumption that we made (twice!) that $\mathsf{RAIN}\land\neg\mathsf{RAIN}$ was discharged by the application of $\neg I$ at the end.

Here’s the derivation to for our running example:

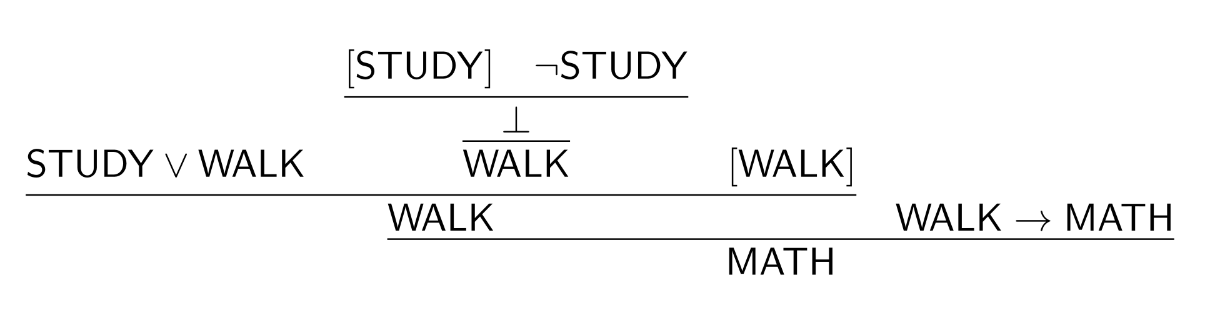
Note that while there are two assumptions that aren’t among our premises, $\mathsf{STUDY}$ and $\mathsf{WALK}$, both are discharged. So, this shows that:

$$\mathsf{STUDY}\lor\mathsf{WALK},\mathsf{WALK}\to\mathsf{MATH},\neg\mathsf{STUDY}\vdash\mathsf{MATH}$$

There are many, many different equivalent natural deduction systems for writing natural deduction proofs. The notation we’re using here is called Prawitz-style natural deduction.

Since the rule $\to E$ is essentially also just MP, we can use chaining algorithms with natural deduction as well.

Resolution-based systems

These are just the most commonly used kind of systems in logical theory. But there are way more different kinds of systems, where especially sequent calculus is of special theoretical importance.

But in the context of logic and AI, we should mention that the resolution algorithm (as well as DPLL), which we studied in the exercises for Chapter 6 , is, essentially, also a proof system.

Remember that the resolution rule, in its most general form, states that if you have two clauses ($l_i,k_j$ are literals)

$$l_1\lor l_2\lor \dots\lor p \qquad \qquad \neg p\lor k_1\lor k_2\lor\dots$$

you can infer:

$$l_1\lor l_2\lor \dots k_1\lor k_2\lor\dots$$

In rule form, we can thus write this as:

$$\begin{array}{ccc} l_1\lor l_2\lor \dots\lor p & & \neg p\lor k_1\lor k_2\lor\dots \\ \hline & l_1\lor l_2\lor \dots k_1\lor k_2\lor\dots \end{array}$$

Written as a rule like this, for formula-formula inferences rather than working with sets of literals, we need to answer one question: What happens if $p$ and $\neg p$ are the only members of their respective clauses? That is, what happens if we have:

$$\begin{array}{ccc} p & & \neg p \\ \hline & ? \end{array}$$

The answer seems to be obvious: in this case, we’ve arrived at a contradiction. So, $?$ should be $\bot$.

The resolution rule in this sense is sound: if the premises are true, then so is the conclusion. In other words, the rule corresponds to a valid inference.

We can, for example, use the resolution rule to check the validity of our running example: $$\mathsf{STUDY}\lor\mathsf{WALK},\mathsf{WALK}\to\mathsf{MATH},\neg\mathsf{STUDY}\vdash\mathsf{MATH}$$ First, we need to use CNF re-writing and equivalently rewrite $\mathsf{WALK}\to\mathsf{MATH}$ as $\neg\mathsf{WALK}\lor\mathsf{MATH}$. Then we can apply resolution as follows:

But the resolution rule alone doesn’t give us an adequate proof system. To see this, note that we can never derive a more complex formula from a simpler formula using resolution. Take for example the valid inference $\mathsf{RAIN}\vDash\mathsf{RAIN}\lor\mathsf{SNOW}$. There is no way to apply the resolution rule to get the conclusion, $\mathsf{RAIN}\lor\mathsf{SNOW}$, from the premise $\mathsf{RAIN}$. To do so, we need to widen our concept of a proof.

So far, we’ve looked at proofs as derivations of formulas from formulas by means of a step-wise arguments. This was a mathematical model of what we might call “direct inference”.

To understand resolution-based systems as proof systems, we need to widen that perspective somewhat: we need to think of a proof as a formal procedure that establishes a valid inference between premises and conclusion:

A proof for $A_1,A_2,\dots\vdash C$ in a resolution-based system is a derivation of $\bot$ from the clauses of the CNF’s of $A_1,A_2,\dots, \neg C$.

This is essentially the idea that we used in the resolution (and DPLL) algorithm, just expressed as a formal proof system: we show that it’s logically impossible to make the premises true and the conclusion false.

In the resulting system, then, we can prove $\mathsf{RAIN}\vDash\mathsf{RAIN}\lor\mathsf{SNOW}$. First, we need to determine the CNF of $\neg(\mathsf{RAIN}\lor\mathsf{SNOW})$, which is just $\neg\mathsf{RAIN}\land\neg\mathsf{SNOW}$. The clauses are therefore $\neg\mathsf{RAIN}$ and $\neg\mathsf{SNOW}$. So, what we need to find is a derivation of $\bot$ from the clauses $\mathsf{RAIN},\neg\mathsf{RAIN},\mathsf{SNOW}$. But that’s just an immediate application of the resolution rule to the first two clauses:

$$\begin{array}{ccc} \mathsf{RAIN} & & \neg \mathsf{RAIN} \\ \hline & \bot \end{array}$$

This shows that in the resolution-based proof system, we get: $$\mathsf{RAIN}\vdash\mathsf{RAIN}\lor\mathsf{SNOW}$$

Applications

The applications of proof systems in science and technology is great. But for AI-purposes, we should highlight at least the following three:

Metalogic

A running theme of the course is the foundational role of logic in AI research: we’re studying valid inference as paradigm intelligent behavior. Proof systems play an important part in this perspective on logic as AI.

The reason for this is that proof systems essentially provide is with a computationally tractable model of step-wise inference: proof systems are precisely defined in finite terms that are easy™️ to implement.

This perspective motivates an interest for AI researchers into metalogical results, especially the so-called soundness and completeness theorems. A proof system is called sound if in the system, only things that actually follow can be derived:

$$P_1,P_2,\dots\vdash C\Rightarrow P_1,P_2,\dots\vDash C$$

This is a sort of “sanity check” for a proof system. A system that doesn’t satisfy soundness, is for obvious reasons not very useful.

Conversely, a system is called complete if in the system all consequences can be derived:

$$P_1,P_2,\dots\vDash C\Rightarrow P_1,P_2,\dots\vdash C$$

Completeness, in contrast to soundness, is not easy to obtain. A complete proof system can derive all consequences, the ones we’ve thought of and the ones we haven’t. This is quite a feat.

A milestone result in metalogical research were the soundness and completeness theorems proved by Kurt Gödel and others. A special case of this result is that the systems we’ve discussed in this chapter are sound and complete with respect to the Boolean algebra semantics:

Soundness and completeness theorem: In propositional logic, we have

$$P_1,P_2,\dots\vDash C\Leftrightarrow P_1,P_2,\dots\vdash C$$

where $\vdash$ denotes derivability in our Hilbert, natural deduction, or resolution system.

A sound and complete system gives an precise characterization of logical consequence in a step-wise computable fashion.

Proof verification

Going more in a practical direction, proof verification is a core application of proof systems in AI. Here, we’re talking about AI in a broader sense, where we’re “outsourcing” intelligent behavior to a computational model. The aim of proof verification is to take mathematical arguments in natural language, calculations and proofs alike, and verify them by showing their validity in a logical proof system.

A proof assistant or interactive theorem prover is a computer program that interactively checks formal arguments provided in a formal language. To illustrate, here are the proofs of our Hilbert $Axioms_{1–3}$ in the interactive theorem prover Lean:

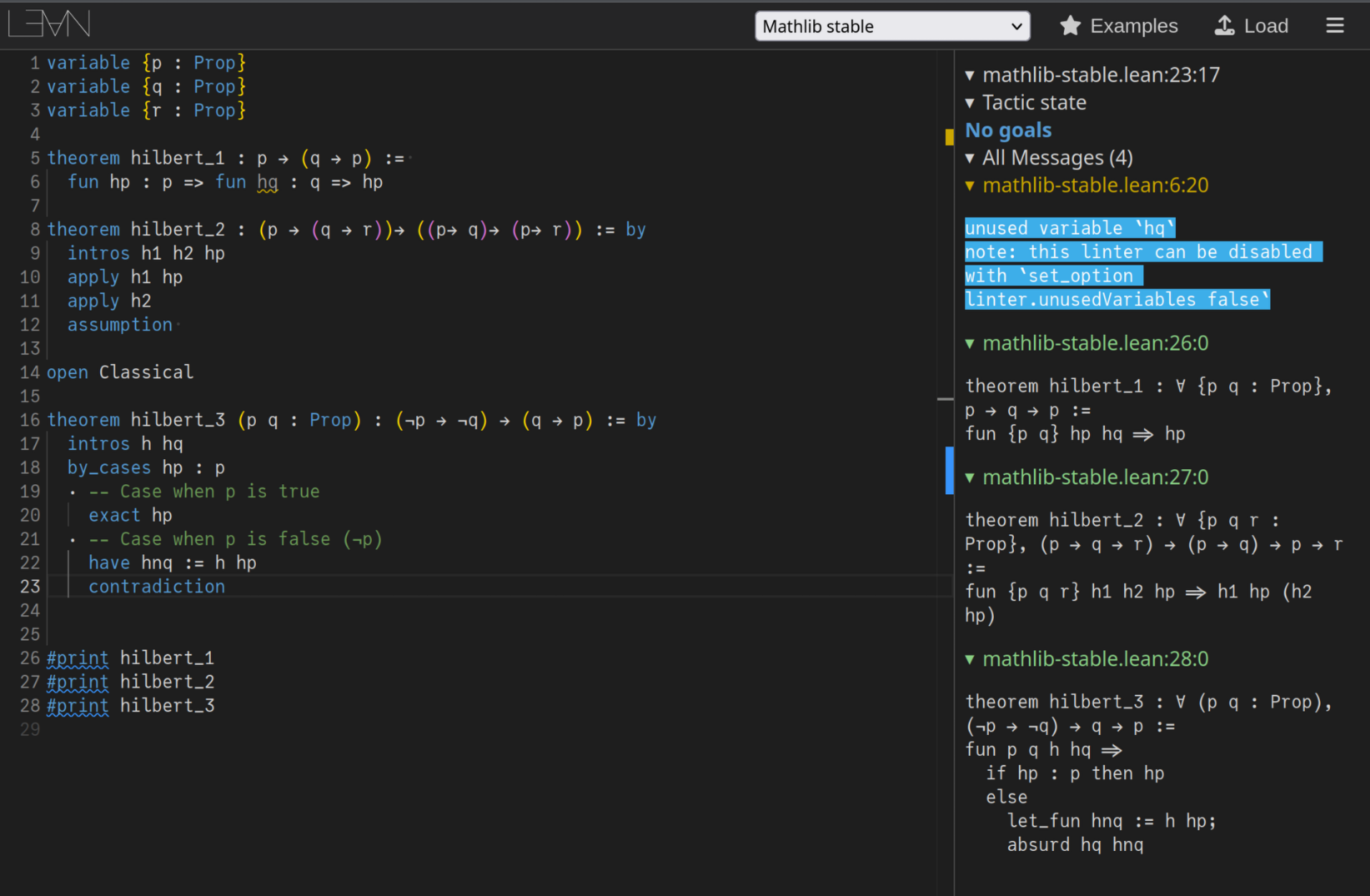
As you can see, Lean works very much like a programming language with an interpreter running “on the side”. In the interpreter window, you can see whether the proof that you’ve so-far is correct.

What’s important to understand is that interactive theorem provers help us to drastically reduce the epistemic burden on checking for correctness of mathematical proofs and complex calculations: any correct mathematical argument can be verified in theorem provers like Lean, so the question of whether a given proof is correct reduces to the question whether the theorem prover used to verify it is correct. We no longer need to check each proof individually, we just need to check the verifier itself.

There is a wide range of proof assistants on the market such as:

The project of formally verifying mathematical results is a very undertaking in current research, which has yielded impressive results like, Lean’s mathlib, and is actively pursued by leading research mathematicians, like Terence Tao.

Automated theorem provers

The final application we should briefly mention is automated reasoning. We’ve already seen some automated reasoning methods, such as satisfiability checking in the context of planning. Automated theorem proving takes another perspective on automated reasoning: it aims to automate mathematical proofs.

A particularly exciting instance of automated reasoning is neural theorem proving, which is a combination of logic-based methods, like interactive theorem provers, and modern sub-symbolic methods. The idea is to train neural networks how to use interactive theorem provers, like Lean. This project has been fairly successful so far and has lead to AI’s that can solve problems from the mathematics Olympiad.