Tutorial 10. Many-valued logics
Exercise sheet
3-valued truth-tables
In Ch. 5. Boolean satisfiability , we’ve described a truth-table method to test for valid inference $P_1,P_2,\dots\vDash C$, which worked by testing whether $P_1\land P_2\land \dots\to C$ is a logical truth in classical logic.
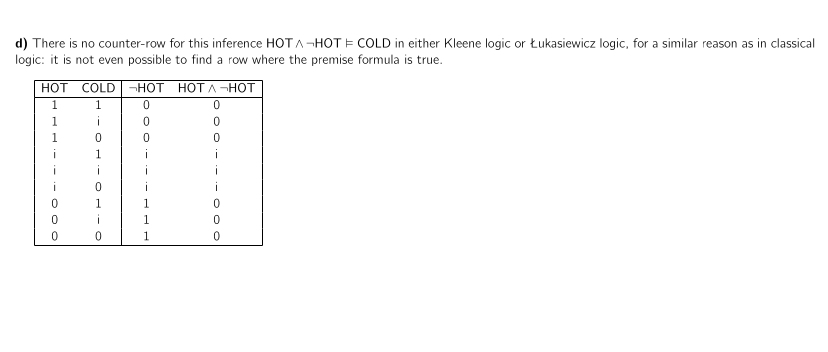
This method doesn’t work in Kleene logic because there are no logical truths but there are valid inferences. But there is an adjusted truth-table method that works for both Kleene and Łukasciewicz.
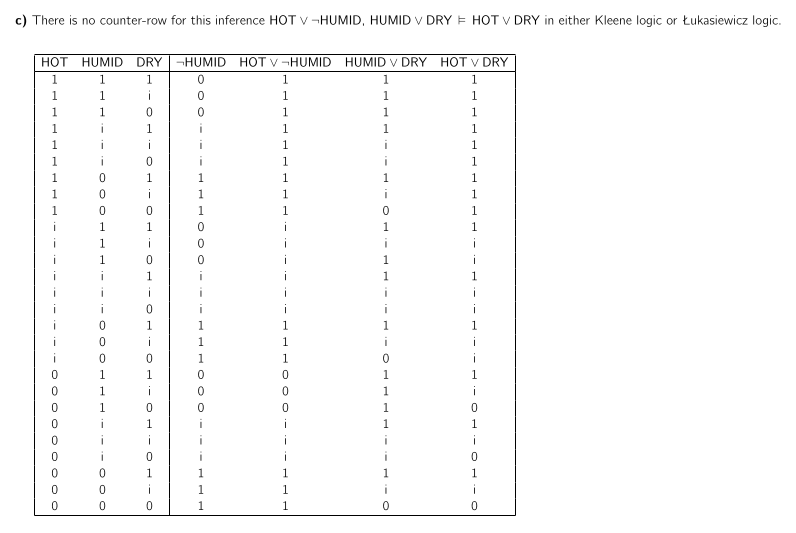
For this method, we need to have one row for each possible assignment of the truth-values $0,i,1$ to the variables in the formula (for $2$ propositional variables that already gives us $3\times 3=9$ rows). Then we recursively calculate the truth-values of both $P_1\land P_2\land \dots$ and $C$ for each row, and we check if in every row where $P_1\land P_2\land \dots$ has value 1, $C$ also has value $1$. If so, the inference is valid, if not it isn’t.
Use this adjusted truth-table method to to determine whether the following inferences are valid in both Kleene and Łukasciewicz logic.
a)
$\mathsf{HOT},\mathsf{HOT}\to \mathsf{HUMID}\vDash \mathsf{HUMID}$
b)
$\mathsf{HOT}\vDash \mathsf{RAIN}\to \mathsf{HOT}$
c)
$\mathsf{HOT}\lor \neg \mathsf{HUMID},\mathsf{HUMID}\lor \mathsf{DRY}\vDash \mathsf{HOT}\lor\mathsf{DRY}$
d)
$\mathsf{HOT}\land \neg \mathsf{HOT}\vDash \mathsf{COLD}$
e)
$\mathsf{HOT}\vDash \mathsf{HUMID}\to\mathsf{HUMID}$
f)
$\neg\mathsf{HOT}\vDash \mathsf{HOT}\to\mathsf{HOT}$
Solutions




Fuzzy logic
Test for each of the following inferences whether it’s valid or not in the fuzzy logic Ł. If the inference is valid, provide an argument, if the inference is invalid provide a countermodel.
a)
$\mathsf{RAIN}\land\neg\mathsf{RAIN}\vDash \mathsf{HOT}$
b)
$\mathsf{HOT}\vDash \mathsf{HOT}\lor(\mathsf{RAIN}\land \mathsf{HOT})$
c)
$\mathsf{HOT}\lor \neg \mathsf{HUMID},\mathsf{HUMID}\lor \mathsf{DRY}\vDash \mathsf{HOT}\lor\mathsf{DRY}$
d)
$\mathsf{HOT}\land \neg \mathsf{HOT}\vDash \mathsf{HOT}$
e)
$\mathsf{HOT}\vDash \mathsf{HUMID}\lor\neg\mathsf{HUMID}$
Solutions
For fuzzy-logic-consequence we check all valuations to see if the smallest premise value will always be lower than the conclusion value. The idea is that this shows us that whenever the premises get ‘closer’ to $1$, the conclusion does too, so there is a truth-strengthening connection between them.
(a) This is invalid. Consider a valuation where $R$ is fuzzy or vague, $v(R)=0.5$, but the conclusion is definitely false $v(H)=0$. Then we have $v(\neg R)=0.5$ and $v(R\land\neg R)=0.5$ which is greater than the conclusion value.
(b) This is valid. We want to show that we always get: $v(H)\leq v(H\lor(R\land H))$.
- Break down the calculation $v(H\lor(R\land H))=\mathrm{max}(v(H),\mathrm{min}(v(R),v(H)))$.
- Consider two ways the atomic parts might be interpreted: $v(H)\leq v(R)$ or $v(H)>v(R)$. Every valuation has to be one of these types. We will show that the result holds on either type.
- If we are looking at the first type of valuation, we have $\mathrm{min}(v(R),v(H))=v(H)$, but that makes $\mathrm{max}(v(H),\mathrm{min}(v(R),v(H)))=\mathrm{max}(v(H),v(H))=v(H)$. So we have $\mathrm{max}(v(H),\mathrm{min}(v(R),v(H)))\leq v(H)$ as desired.
- If we are looking at the second type of valuation, we have $\mathrm{min}(v(R),v(H))=v(R)$, but that makes $\mathrm{max}(v(H),\mathrm{min}(v(R),v(H)))=\mathrm{max}(v(H),v(R))=v(H)$. Again, we have $\mathrm{max}(v(H),\mathrm{min}(v(R),v(H)))\leq v(H)$ as desired.
(c) This is invalid. Consider a valuation where $U$ is fuzzy or vague, $v(U)=0.5$, but the other statements are definitely false $v(H)=0$ and $v(D)=0$. Then we have $v(H\lor\neg U)=\mathrm{max}(v(H),1-v(U))=0.5$. We also have $v(U\lor D)=\mathrm{max}(v(U),v(D))=0.5$. Take the minimum $\mathrm{min}(\mathrm{max}(v(H),v(\neg U)),\mathrm{max}(v(U),v(D)))=0.5$. But this value is greater than the conclusion value $v(H\lor D)=\mathrm{max}(v(H),v(D))=0$, so we have a counter-model.
(d) This is valid. We want to show that we always get: $v(H\land\neg H)\leq v(H)$. It’s immediate from $v(H\land\neg H)=\mathrm{min}(v(H),1-v(H))$. This guarantees that the premises cannot exceed the value of H itself.
- To illustrate, suppose that $v(H)=0$ then we get $v(H\land\neg H)= 0$.
- Suppose that $v(H)=0.1$ then we get $v(H\land\neg H)= 0.1$.
- Suppose that $v(H)=0.5$ then we get $v(H\land\neg H)= 0.5$.
- Suppose that $v(H)=0.9$ then we get $v(H\land\neg H)= 0.1$.
- Suppose that $v(H)=1$ then we get $v(H\land\neg H)= 0$.
Fuzzy rules
Remember that a fuzzy rule $$\textbf{IF } A \textbf{ THEN } B$$ means that $B$ holds to the extend that $A$.
Imagine an HVAC -system, with a fuzzy control unit. We want the system to behave as follows:
- If it’s hot or humid, then power up the AC unit.
- If it’s cold or humid, then power up the heating unit.
- If you power up the AC unit, power down the heating unit.
- If you power up the heating unit, power down the AC unit.
a)
Using only the propositional variables
$$\mathsf{HOT},\mathsf{HUMID},\mathsf{AC},\mathsf{HEAT}$$
formule fuzzy rules that represent our fuzzy control rules from above.
b)
Check whether the rules behave reasonably by going through what happens with some concrete numerical values representing:
- hot high, humidity high
- hot medium, humidity high
- hot low, humidity high
- hot high, humidity medium
- hot medium, humidity medium
- hot low, humidity medium
- hot high, humidity low
- hot medium, humidity low
- hot low, humidity low
Are there any problematic cases? If so, can we fix them?
Solutions
(a) Here is the best way to write the rules in our limited formal language. Remember, we want to interpret these like fuzzy-logic-consequence: whenever the antecedent side gets ‘closer’ to $1$, we want the conclusion to do the same.
IF HOT$\lor$HUMID, THEN AC
IF $\neg$HOT$\lor$HUMID, THEN HEATER
IF AC, THEN $\neg$HEATER
IF HEATER, THEN $\neg$AC
(b) One example of a problem for these rules: situations with low heat and high humidity. To be precise, consider a valuation where $v(\mathsf{HOT})=0.2$ and $v(\mathsf{HUMID})=0.8$. This makes $v(\neg\mathsf{HOT})=1-v(\mathsf{HOT})=0.8$.
We calculate $v(\mathsf{HOT}\lor\mathsf{HUMID})=0.8$.
So the first rule requires $0.8\leq v(\mathsf{AC})$.
We also calculate $v(\neg\mathsf{HOT}\lor\mathsf{HUMID})=0.8$.
So the second rule requires $0.8\leq v(\mathsf{HEATER})$.
This is okay so far, but the final rules create a problem.
For instance, the last rule requires $0.8\leq 1-v(\mathsf{AC})$.
There is no value that gives $0.8\leq v(\mathsf{AC})$ and $0.8\leq 1-v(\mathsf{AC})$.
So these rules do not ‘work’ as intended in all possible fuzzy valuations.
T-norms
The general theory of fuzzy logics uses the concept of a t-norm , which is short for “triangular norm.” T-norms are used to define a fuzzy conditional that behaves in a natural way as a “logical” conditional for fuzzy logic. These logical conditionals of fuzzy find applications in fuzzy knowledge bases, where they allow the application of chaining methods for example.
We’ll not go into the details of the construction of the conditional here, but rather focus on what the t-norm for Łukasiewicz fuzzy logic.
a) Strong conjunction
The t-norm for fuzzy logic can be expressed by introducing an extra connective $\otimes$ (“strong conjunction”) to the language with $\neg,\land,\lor$. This connective uses the fuzzy truth-function: $$f_\otimes(x,y)=\max(0,x+y-1).$$ That is the recursive truth-values for $A\otimes B$ are calculated as follows:
$$\nu(A\otimes B)=\max(0,\nu(A)+\nu(B)-1).$$
Check that the following characteristic properties hold for the operation $f_\otimes$:
- $f_\otimes(x,y)=f_\otimes(y,x)$
- If $x\leq x’$ and $y\leq y’$, then $f_\otimes(x,y)\leq f_\otimes(x’,y’)$
- $f_\otimes(x,f_\otimes(y,z))=f_\otimes(f_\otimes(x,y),z)$
- $f_\otimes(x,1)=x$
Hint: Here you cannot check all possible cases, since $x,y,z\in\mathbb{R}$ can take infinitely many values. Instead, you need to reason “algebraically” about how the values hang together. Here are some tips on what to use:
-
For the first, you need to use the mathematical fact that $x+y=y+x$.
-
For the second, you need to consider the cases where $f_\otimes(x,y)$ can be $0$ and the mathematical fact that sums of bigger numbers are bigger.
-
For the third, you need to use the fact that $x+(y+z)=(x+y)+z$.
-
For the fourth, you’re on your own 😃
b) Fuzzy logical conditional
In Łukasiewicz’s logic, the logical conditional $\to$ is interpreted by the following truth-function:
$$f_\to(x,y)=\min(x,1-x+y)$$
That means that:
$$\nu(A\to B)=\min(x,1-\nu(A)+\nu(B))$$
Check that the following holds in Łukasiewicz’s logic:
$$\mathsf{RAIN}\otimes (\mathsf{RAIN}\to \mathsf{WET})\vDash \mathsf{WET}$$
Solution
(a) Strong Conjunction.
The $f_\otimes$ function calculates its output in two different ways, depending on the input values. We get a default value $f_\otimes(x,y)=0$ when $x+y\leq 1$, but we get $f_\otimes(x,y)=x+y-1$ when $1<x+y$. For these exercises we prove both cases separately.
(1) We prove the goal in two cases using $x+y=y+x$.
-
If $f_\otimes(x,y)=0$ then $x+y\leq 1$. This implies that $y+x\leq 1$ and so $f_\otimes(y,x)=0$.
-
If $f_\otimes(x,y)\neq 0$ then $f_\otimes(x,y)=x+y-1=y+x-1=f_\otimes(y,x)$.
(2) We prove the goal in two cases.
-
If $f_\otimes(x,y)=0$ then obviously $f_\otimes(x,y)\leq f_\otimes(x’,y’)$.
-
If $f_\otimes(x,y)\neq 0$ then we reason:
- $x\leq x’$ and $y\leq y’$
- so we have $x+y\leq x’+y’$
- so we have $x+y-1\leq x’+y’-1$
- therefore $f_\otimes(x,y)\leq f_{\oplus}(x’,y’)$
(3) We prove the goal in two cases using $x+(y+z)=(x+y)+z$.
-
If $f_\otimes(x,f_\otimes(y,z))=0$ then SOMETHING
-
If $f_\otimes(x,y)\neq 0$ then we reason: SOMETHING
(4) We prove the goal in two cases.
-
If $f_\otimes(x,1)=0$ this means that $x+1\leq 1$ and so $0=x$.
-
If $f_\otimes(x,1)\neq 0$ then $f_\otimes(x,1)= x+1-1 = x$.
(b) Fuzzy Conditional.
The $f_\to$ function calculates its output in two different ways, depending on the input values. We default to the antecedent value $f_\to(x,y)=x$ when $2x-y\leq 1$, but we get $f_\to(x,y)=1-x+y$ when $1<2x-y$.
For fuzzy-logic-consequence we check all valuations to see if the smallest premise value will always be lower than the conclusion value. So we want to show that we always get: $v(R\otimes (R\to W))\leq v(W)$.
Break down the calculation $v(R\otimes (R\to W))=f_\otimes(v(R),v(R\to W))=f_\otimes(v(R),f_\to(v(R),v(W)))$.
We can think about how $f_\otimes(v(R),f_\to(v(R),v(W)))$ is calculated in two ways.
- The first possibility is quick: If $f_\otimes(v(R),f_\to(v(R),v(W)))=0$ then obviously $v(R\otimes (R\to W))\leq v(W)$.
- The second possibility requires more thinking: suppose that $f_\otimes(v(R),f_\to(v(R),v(W)))\neq 0$.
- That means $f_\otimes(v(R),f_\to(v(R),v(W)))=v(R)+f_\to(v(R),v(W))-1$.
- We now think about how $f_\to(v(R),v(W))$ is calculated in two ways.
- First, if $2v(R)-v(W)\leq 1$ that gives us two pieces of information. We have $f_\to(v(R),v(W))=v(R)$ which plugs into our original calculation to give us $f_\otimes(v(R),f_\to(v(R),v(W)))=2v(R)-1$ and we also have $2v(R)-1\leq v(W)$. It follows that $f_\otimes(v(R),f_\to(v(R),v(W)))\leq v(W)$.
- Second, if $1<2v(R)-v(W)$, then $f_\to(v(R),v(W))=1-v(R)+v(W)$ and $f_\otimes(v(R),f_\to(v(R),v(W)))=v(R)+(1-v(R)+v(W))-1=v(W)$. It follows that $f_\otimes(v(R),f_\to(v(R),v(W)))\leq v(W)$.
Research
Find out what fuzzy sets are.
a)
How are fuzzy sets related to fuzzy logic?
b)
How are fuzzy sets used in AI?
Discussion
Kleene logic has no logical laws/tautologies, as discussed in class. For example, if we don’t know whether it’ll rain or now and model this by $$\nu(\mathsf{RAIN})=i,$$ in Kleene’s logic, we’ll get the consequence that $$\nu(\mathsf{RAIN}\lor\neg\mathsf{RAIN})=i.$$ In a sense, this is what we want (we don’t know whether it’ll rain or not), but in a sense this is also unsatisfactory: we know that one of the two will happen, we just don’t know which. Is this a problem for applications of Kleene logic in AI-decision making systems? Argue your answer in one or two paragraphs.