logicalmethods.ai – Boolean algebra

Tutorial 4. Boolean algebra

Exercise sheet

Relay logic

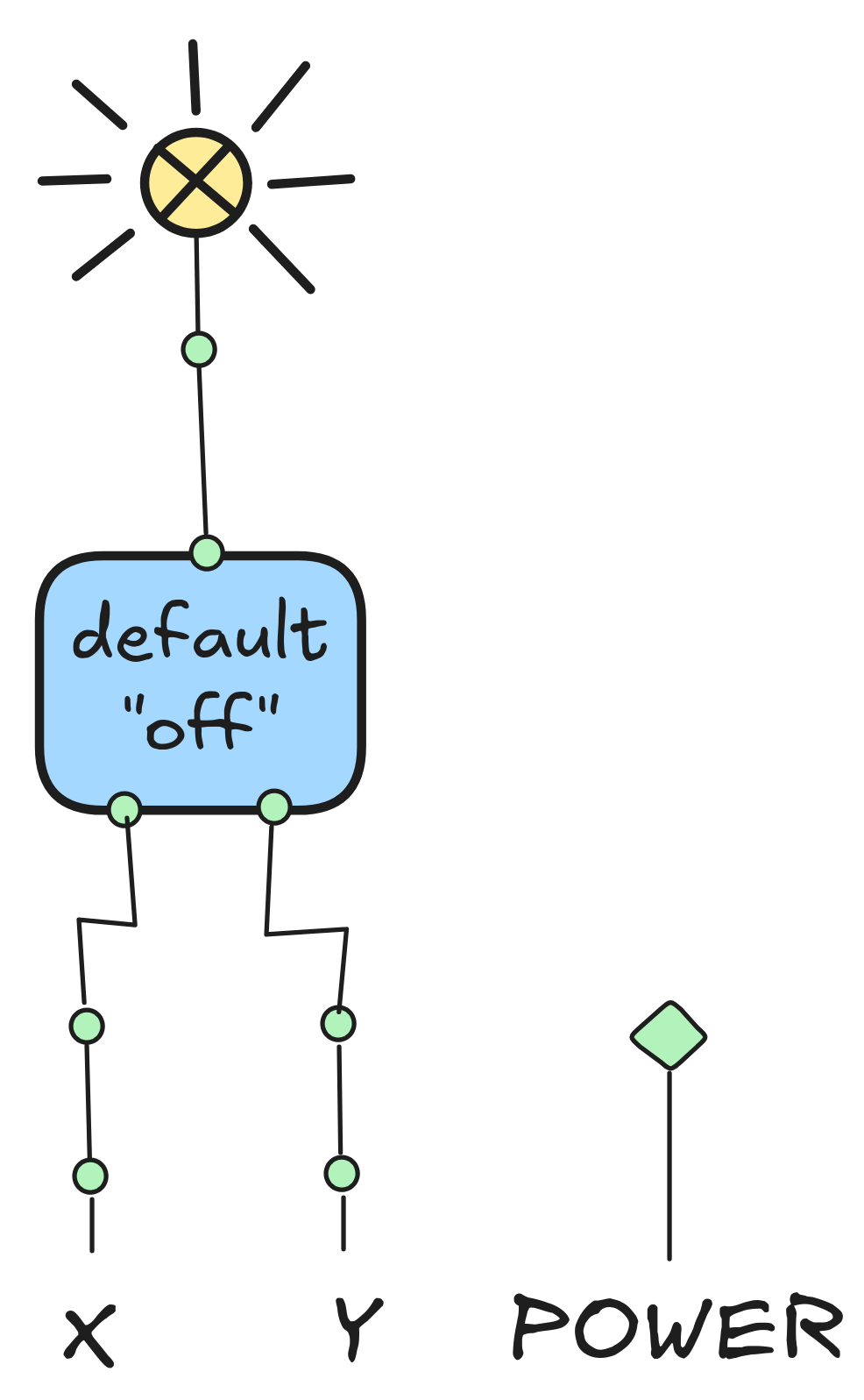
In the chapter you’ve learned about relay logic, that is the implementation of the Boolean functions using the default “off” and default “on” relay:

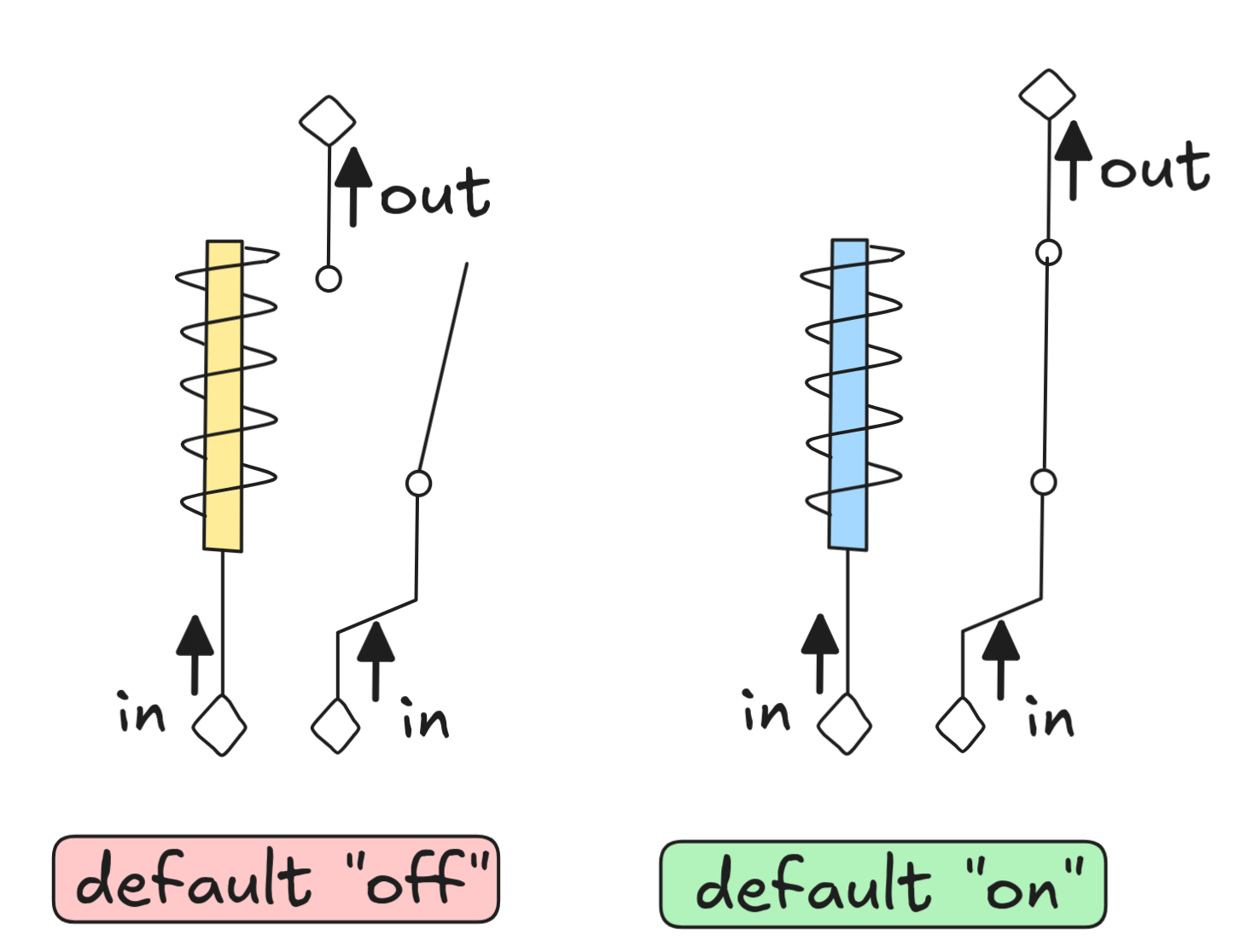
We showed how to make circuits which behave just like NOT and AND using these relays. As a reminder, here are the concrete implementations:

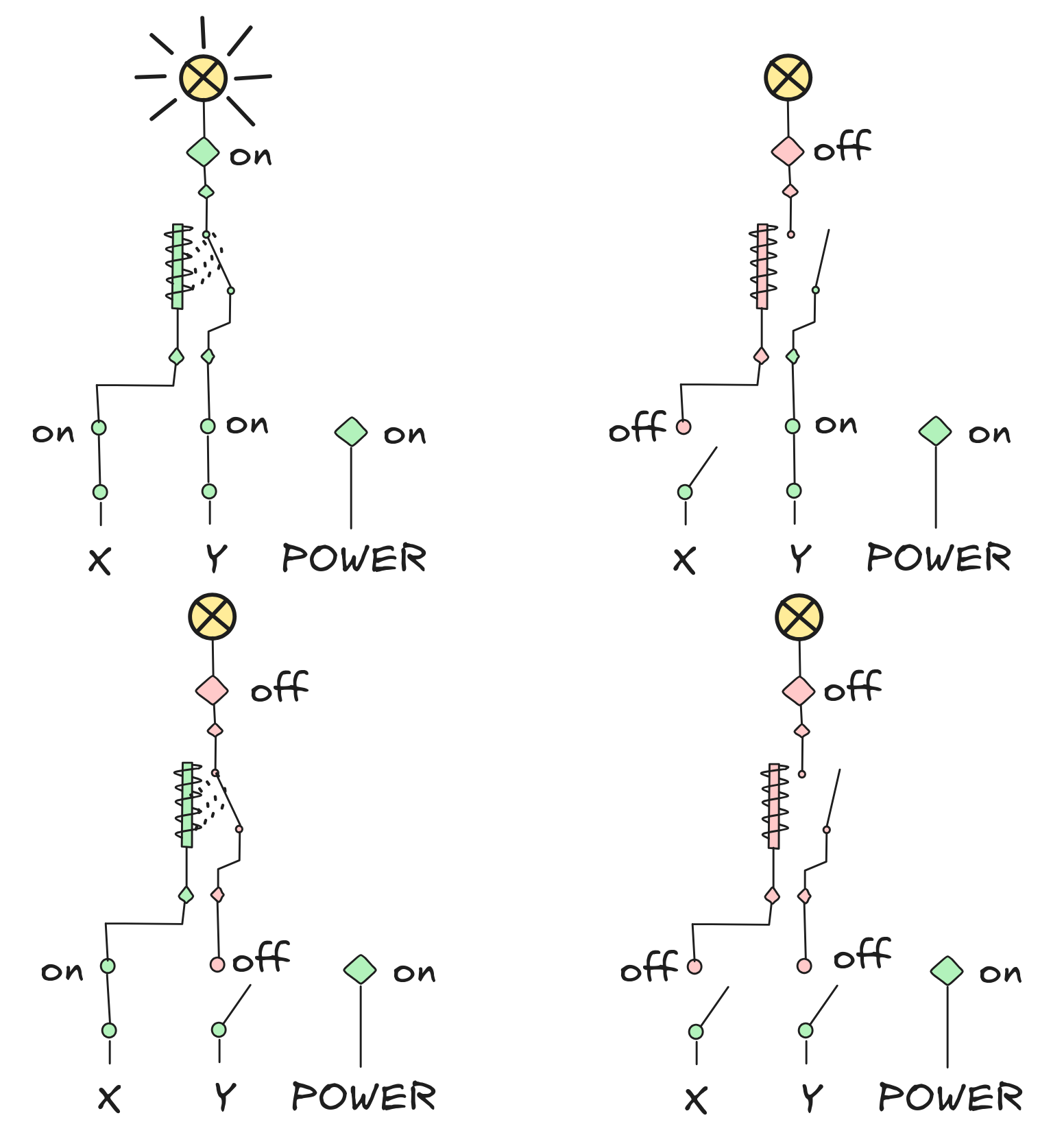
Note that we’ve depicted all possible configurations of the relay to demonstrate that the circuit behaves “according to spec”, that is: just like the corresponding Boolean truth-function.

For this exercise, you’ll implement some more Boolean truth-functions using relays. You can draw the diagrams in whatever way works and clearly illustrates the idea. To show what I mean, here’s one way to simplify the diagram for the AND-circuit (in the configuration for both inputs being 1):

Make sure that to verify that your circuit is according to spec! Note that you may need both kinds of relays for the implementations.

Implement OR

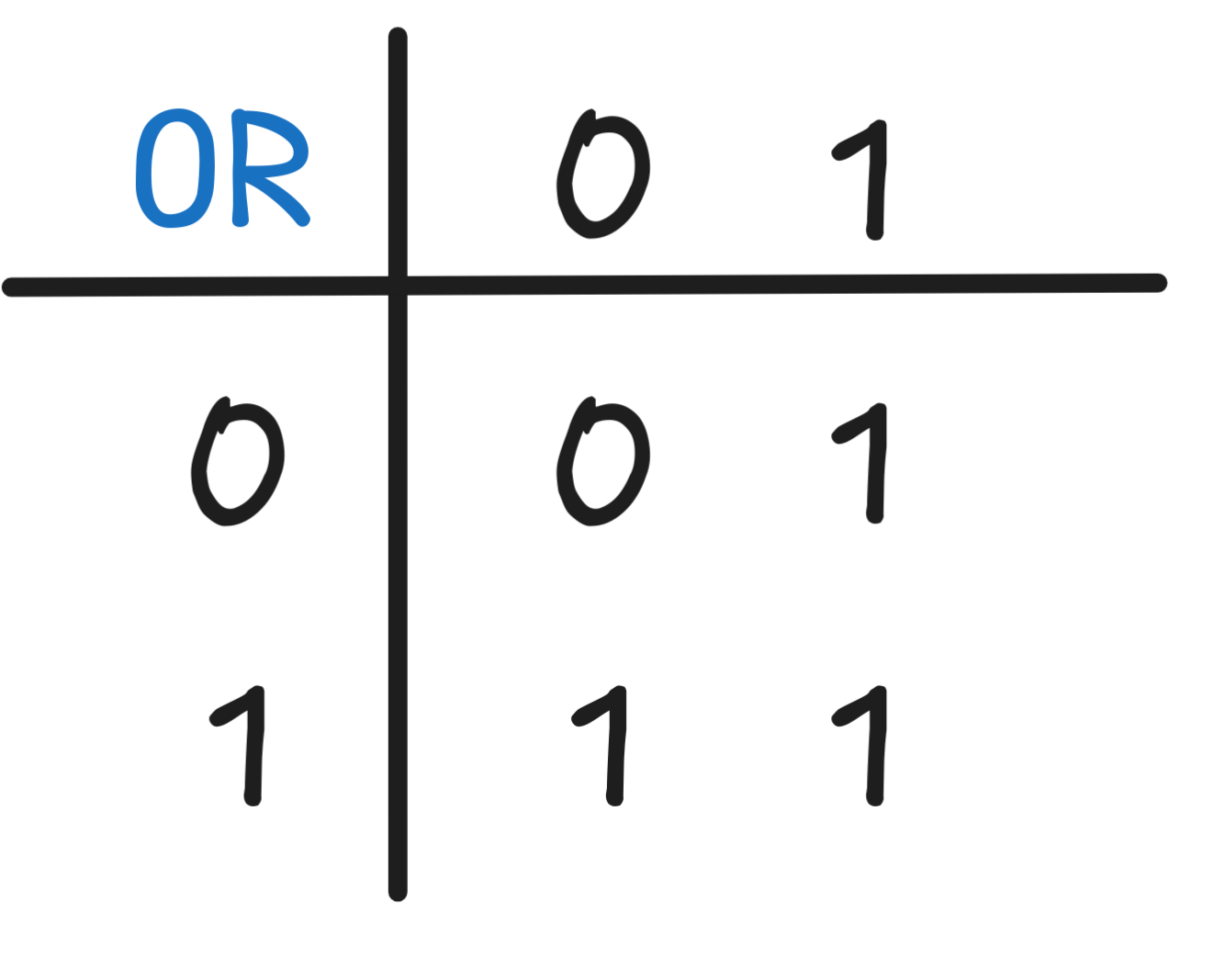
Implement NAND

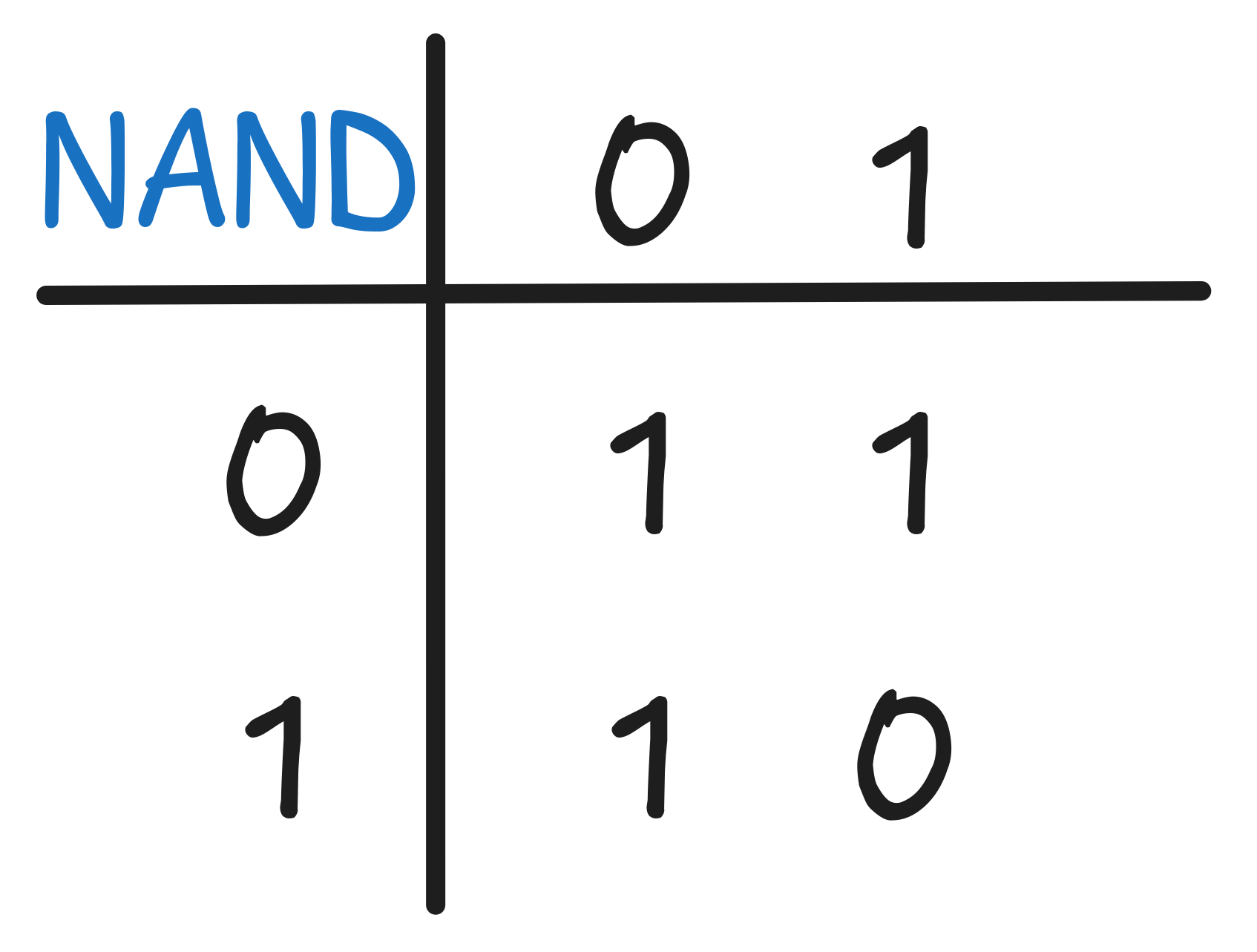
Implement XOR

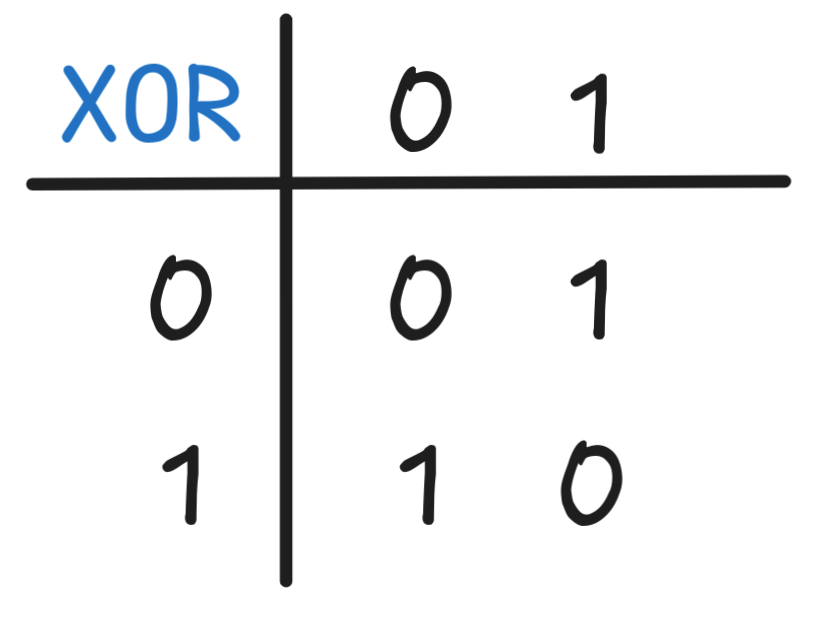
Solution

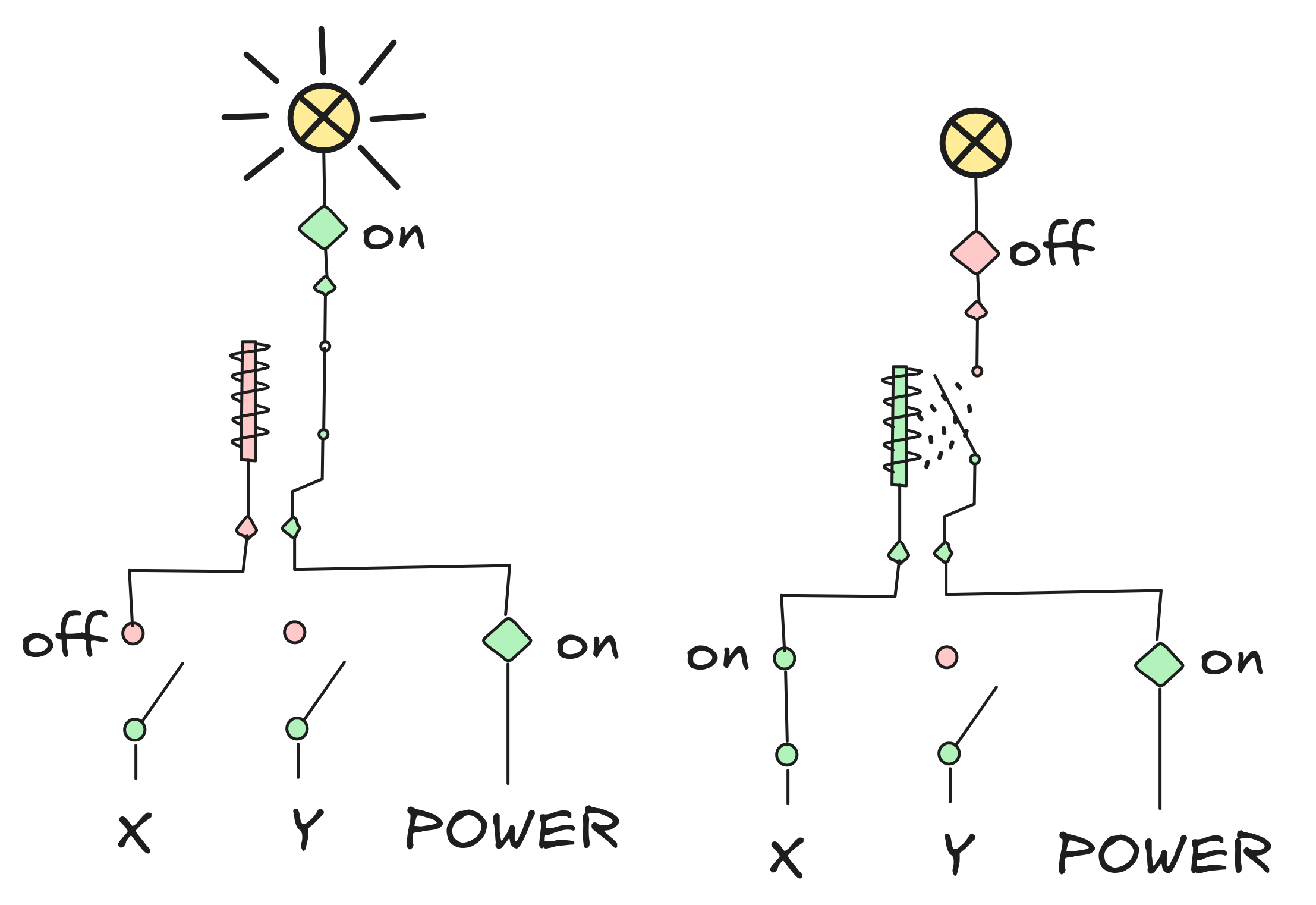
Here are some implementations. They re not the only ones, they illustrate different ideas. What matters is that your circuit works:

An OR implementation, which uses the idea that X OR Y is NOT ((NOT X) AND (NOT Y)):

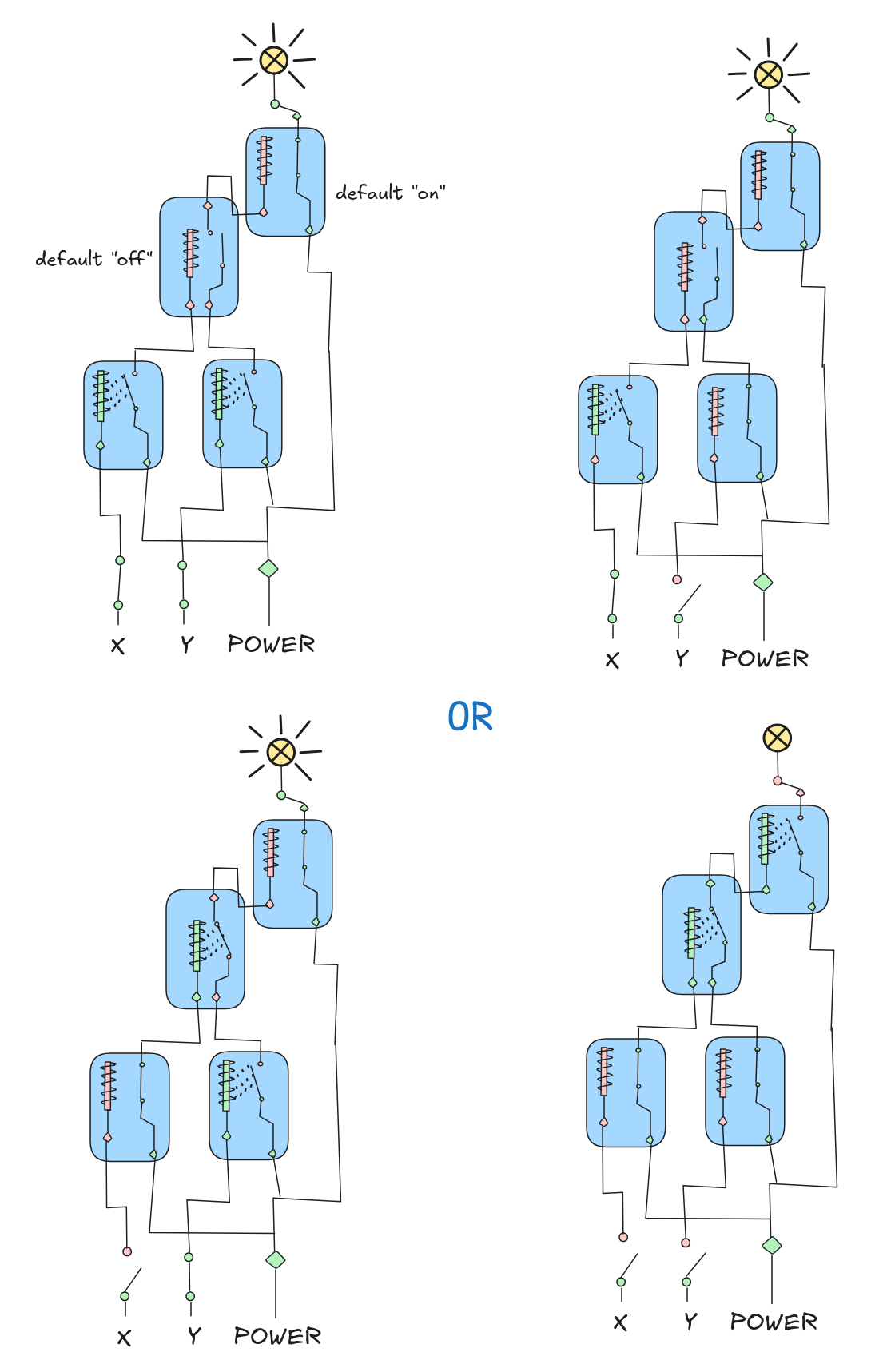
A NAND implementation, which is based on the observation that default “off” is essentially AND and default “on” essentially NOT:

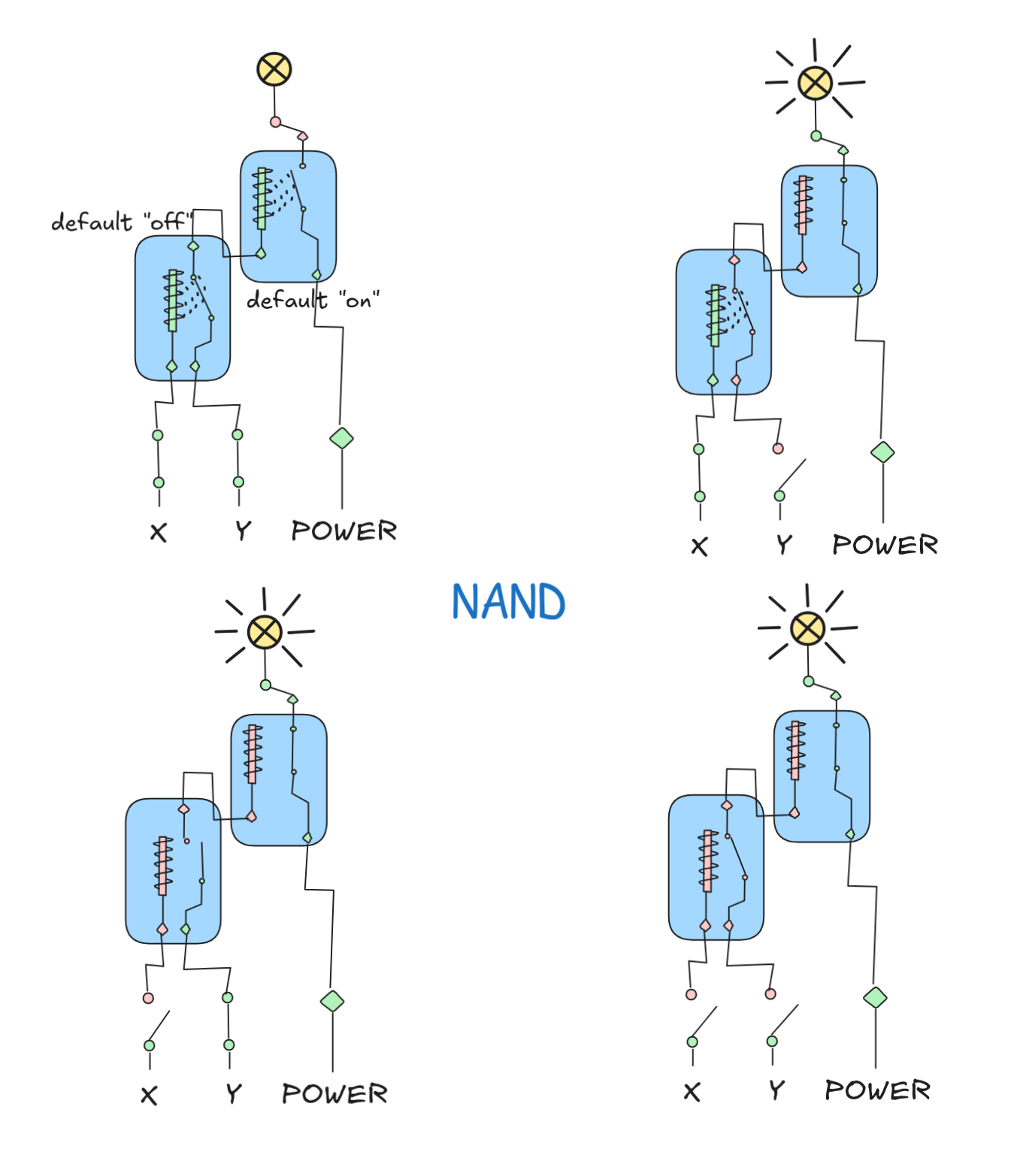
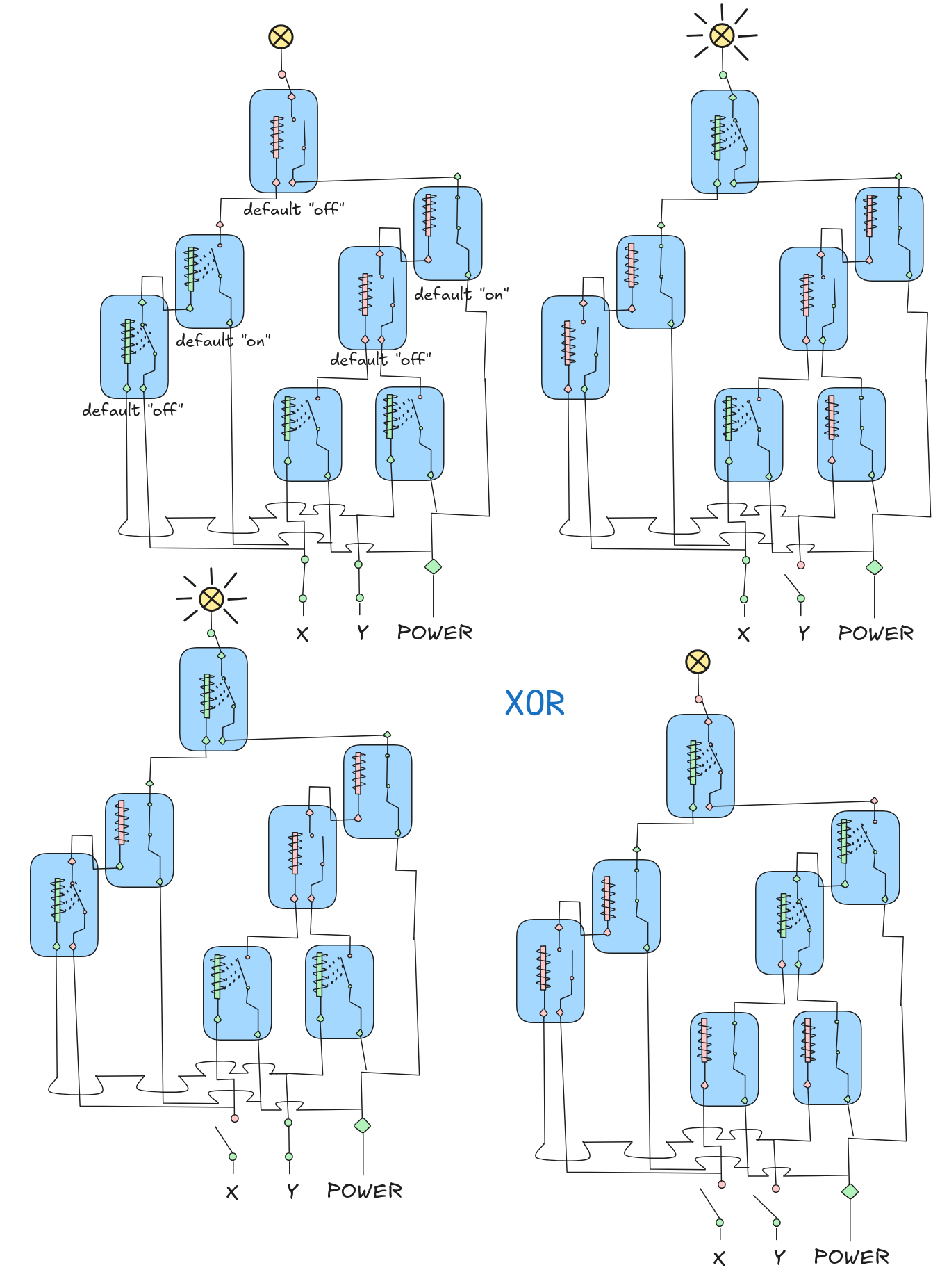
An XOR implementation, based on the idea that X XOR Y is (X OR Y) AND (X NAND Y):

Defining functions

We’ve mentioned the idea of truth-functional completeness: we can express all truth-functions purely in terms of NOT, AND, and OR.

To illustrate what this means, here’s how we express OR in terms of NOT and AND. First, we write OR as a Boolean expression with two variables, which represent the two inputs:

Using the function table for OR, we can calculate the value of this expression for all values of X and Y. The representation of OR in terms of NOT and AND is, then, the following Boolean expression:


NOT ((NOT X) AND (NOT Y))

We (by which I mean you 😉), we can verify this by going through the possible values for X and Y and check that for each such value, we have that:


X OR Y = NOT ((NOT X) AND (NOT Y))

Verify this equation for all values of X and Y.
Represent XOR in terms of NOT, AND, and OR.
Represent NAND in terms of NOT and AND.
Here’s an interesting one: represent NOT in terms of NAND.

Solution

Here are the calculations for all values:
- X = 1, Y = 1: NOT ((NOT 1) AND (NOT 1)) = NOT (0 AND 0) = NOT 0 = 1
- X = 0, Y = 1: NOT ((NOT 0) AND (NOT 1)) = NOT (1 AND 0) = NOT 0 = 1
- X = 1, Y = 0: NOT ((NOT 1) AND (NOT 0)) = NOT (0 AND 1) = NOT 0 = 1
- X = 0, Y = 0: NOT ((NOT 0) AND (NOT 0)) = NOT (1 AND 1) = NOT 1 = 0
This is exactly the distribution of OR.
Here’s a representation: (X OR Y) AND NOT (X AND Y)
- X = 1, Y = 1: (1 OR 1) AND NOT (1 AND 1) = 1 AND (NOT 1) = 1 AND 0 = 0
- X = 0, Y = 1: (0 OR 1) AND NOT (0 AND 1) = 1 AND (NOT 0) = 1 AND 1 = 1
- X = 1, Y = 0: (1 OR 0) AND NOT (1 AND 0) = 1 AND (NOT 0) = 1 AND 1 = 1
- X = 0, Y = 0: (0 OR 0) AND NOT (0 AND 0) = 0 AND (NOT 0) = 0 AND 1 = 0
Here’s a representation: NOT (X AND Y)!!
- X = 1, Y = 1: NOT (1 AND 1) = NOT!! 1 = 0
- X = 0, Y = 1: NOT (0 AND 1) = NOT!! 0 = 1
- X = 1, Y = 0: NOT (1 AND 0) = NOT!! 0 = 1
- X = 0, Y = 0: NOT (0 AND 0) = NOT!! 0 = 1
You can just use:
X NAND X
because
- X = 1: 1 NAND 1 = 0
- X = 0: 0 NAND 0 = 1

Boolean laws

Use the laws of Boolean algebra to derive the following equation:


X AND (X OR Y) = X OR (X AND Y)

Solution

This is rather straight-forward: just note that both sides are equal to X by the law of “Absorption”.

Addition

We’ve studied how you can add two numbers in binary. We’ll use this to verify the equation:

5 + 7 = 12.

Transform the summands 5 and 7 into binary notation. The result will be 3-bit binary numbers.
Calculate each bit of the sum step by step using the Boolean functions for the full adder (note that you must initialize the carry to 0 for the first calculation to work).

Solution

Here are the two numbers in binary:
- 5 in binary is 0101 since (0 x 2³) + (1 x 2²) + (0 x 2¹) + (1 x 2⁰) = 0 + 4 + 0 + 1 = 5
- 7 in binary is 0111 since (0 x 2³) + (1 x 2²) + (1 x 2¹) + (1 x 2⁰) = 0 + 4 + 2 + 1 = 7
Here are the calculations, where dᵢ is the i-th digit of 5 in binary, and eᵢ is the i-th digit of 7 in binary, and cᵢ is the i-th carry bit:
- 0-th bit:
  - sum bit: (d₀ XOR e₀) XOR 0 = (1 XOR 1) XOR 0 = 0 XOR 0 = 0
  - carry bit =(d₀ AND e₀ ) OR (0 AND (d₀ XOR e₀)) = (1 AND 1) OR (0 AND (1 XOR 1) = 1 OR (0 AND 0) = 1 OR 0 = 1
- 1-th bit:
  - sum bit: (d₁ XOR e₁) XOR c₀ = (0 XOR 1) XOR 1 = 1 XOR 1 = 0
  - carry bit = (d₁ AND e₁ ) OR (c₁ AND (d₁ XOR e₁)) = (0 AND 1) OR (1 AND (0 XOR 1) = 0 OR (1 AND 1) = 0 OR 1 = 1
- 2-th bit:
  - sum bit: (d₂ XOR e₂) XOR c₁ = (1 XOR 1) XOR 1 = 0 XOR 1 = 1
  - carry bit = (d₂ AND e₂ ) OR (c₁ AND (d₂ XOR e₂)) = (1 AND 1) OR (1 AND (1 XOR 1)) = 1 OR (1 AND 0) = 1 OR 0 = 1
- 3-th bit:
  - sum bit: (d₃ XOR e₃) XOR c₂ = (0 XOR 0) XOR 1 = 0 XOR 1 = 1
  - carry bit = (d₃ AND e₃) OR (c₂ AND (d₃ XOR e₃)) = (0 AND 0) OR (1 AND (0 XOR 0) = 0 OR (1 AND 0) = 0 OR 0 = 0
  So the result is 1100, which is 12 since (1 x 2³) + (1 x 2²) + (0 x 2¹) + (0 x 2⁰) = 8 + 4 + 0 + 0 = 12.

Models

Suppose that we have a language L with three propositional variables RED, BLUE, and GREEN, which we use to reason about the color of a pixel in the RGB color model .

Determine all the valuations for that language.
If we change our language RED₁, BLUE₁, and GREEN₁ to talk about the color of a first pixel, and RED₂, BLUE₂, and GREEN₂ to talk about the color of a second pixel, what happens to the number of valuations? Don’t determine them all, just think about what happens.
How many valuations are there in the language that has a propositional variable for each RGB-value of each pixel on a 4K-resolution screen . (You can’t actually calculate that value, but you can write an expression that represents it.)

Solution

There are 2⁴ = 8 total valuations for that language. We can give them in the following table:

	RED	GREEN	BLUE
v₁:	1	1	1
v₂:	1	1	0
v₃:	1	0	1
v₄:	1	0	0
v₅:	0	1	1
v₆:	0	1	0
v₇:	0	0	1
v₈:	0	0	0

We now have 2⁶ = 64 valuations. One way of seeing this is that there are 8 ways of distributing the truth-values over 3 propositional variables. That means that if we double the number of variables to 6, we can combine each of the original assignments with one of the new ones, which means we have 8 x 8 = 64 assignments.
This would give us 2 to the power of 3 x 8,294,400 many valuations. This number is huge enough so that we can’t write it down. Ever.

Each such valuation would correspond to an image on a 4K-screen. So that’s the total number of possible images on a 4K-screen 😃.

Deductive inference

Translate the inference into a suitable formal language.
Determine whether the formal inference is valid using Boolean logic.

Solution

Here’s a formal representation of the inference in the propositional language with propositional variables SCHOOL and HOME to say that little Jimmy is at school and home, respectively:
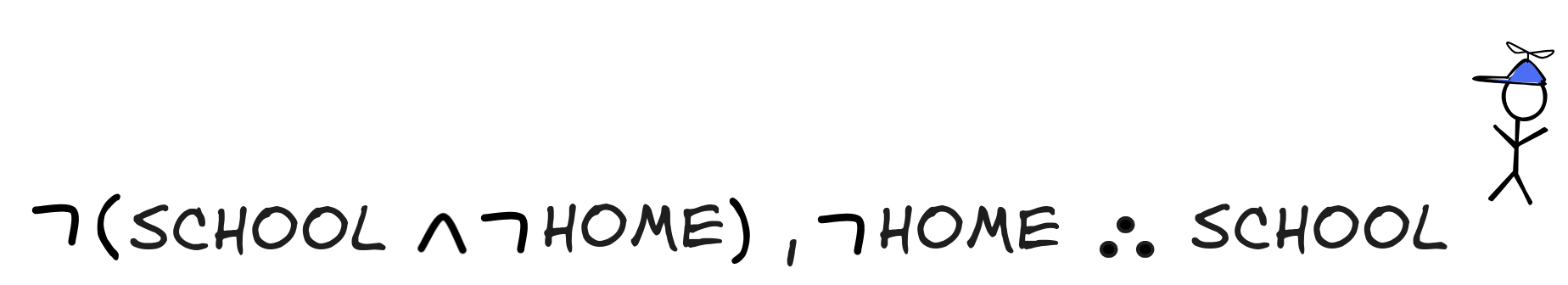
To see check whether the inference is valid, we need to go through all possible valuations of the language and see if whenever the premises are true, so is the conclusion. There are four possible valuations, given by the following table:

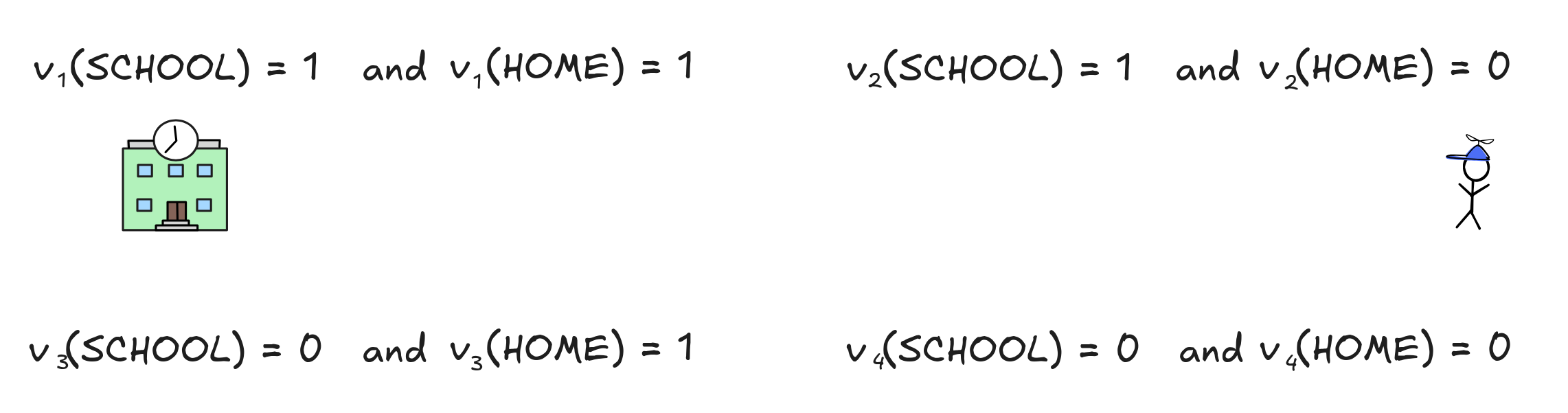
The value of the formulas involved are calculated as follows:

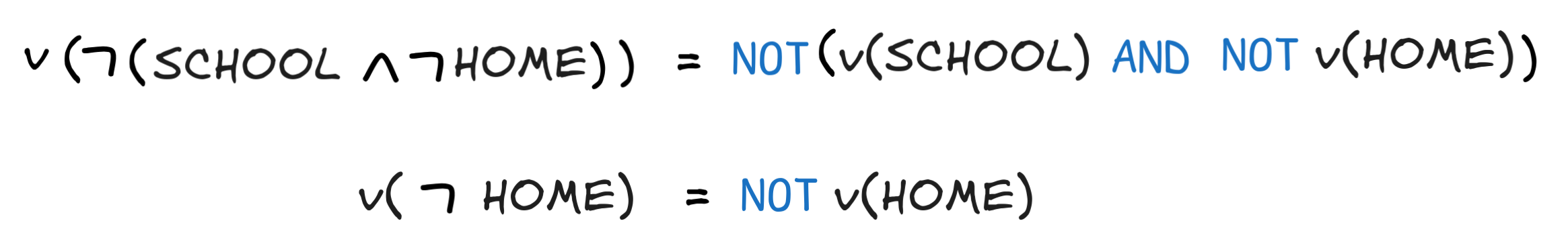
So, for each possible v, we can calculate the values of the premises using Boolean algebra:

Inspecting the possible values, we can find a valuation where both premises are true and the conclusion is false, viz. v₄, where Jimmy is neither at school nor at home.

But that means that the set of valuations where both premises are true is not a subset of the set of valuations where the conclusion is true:

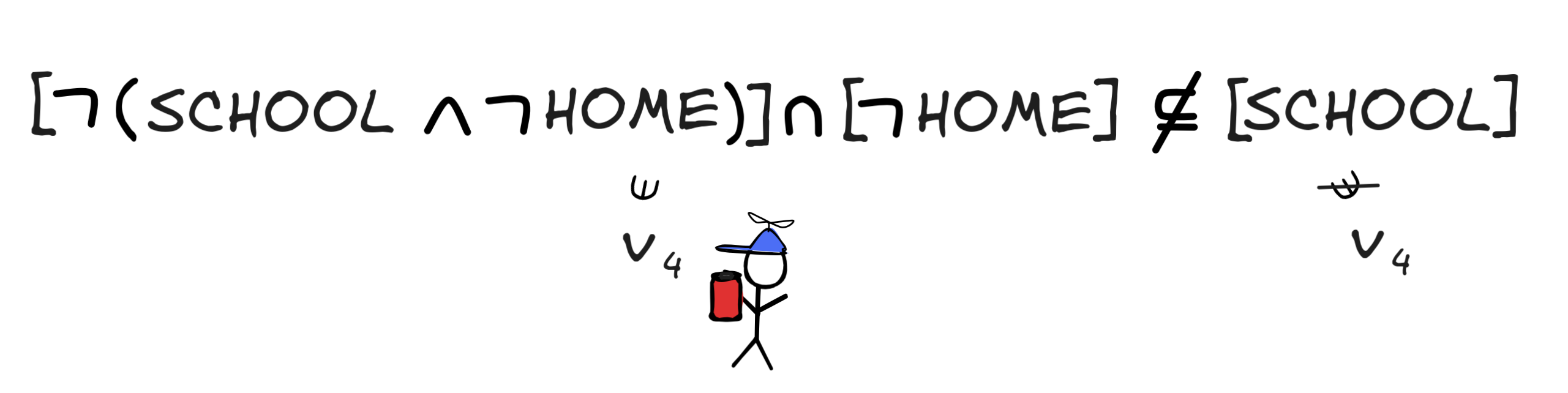
In other words, the inference is invalid:

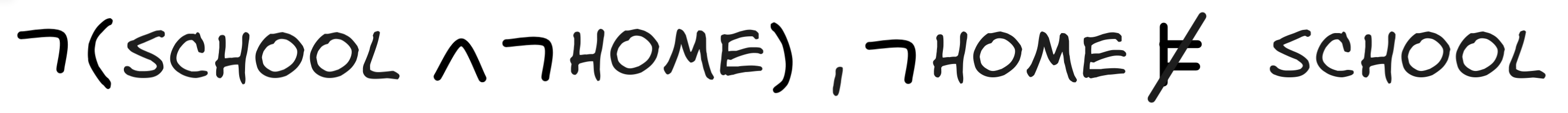
Logical laws

So far, we’ve only shown of particular inferences (about the weather or little Jimmy) that they are valid or invalid. For this exercise, you’ll show that all inferences of a certain form are valid, regardless what they’re about.

For this, we’ll focus on disjunctive syllogism, which we take to be the following inference schema, where A and B can be any two formulas whatsoever:

To show that this inference is valid, following the definition of deductive validity, we need to show that:

This means, according to the definition of ⊆, that we need to show that any valuation v:

If v

, then v

This is the claim, we’ll set out to show:

Assume that v is an arbitrary valuation, meaning you don’t know anything about, such as which values it assigns to which formula. Assume further that v A B A . Apply the definition of
A = { v : v(A) = 1},
as well as the definition of intersection as

S T = { x : x S and x T}

to infer what this means for the values of A v B and ¬A under v.
Using the general clauses for calculating the values under an assignment,

v( A) = NOT v(A)

v(A B) = v(B) AND v(A)

v(A B) = v(A) OR v(A)

to transform the result of a last step into two Boolean equations.
“Solve” this Boolean equation for the value v(B) of B, that is infer what that value must be. Conclude from this that v B and the inference is valid.

Solution

Let v be a valuation such that v A B A . By the definition of , this means that v A B and v A . And by the definition of , this means that v(A B) = 1 and v( A) = 1.
Applying the clauses, we get:
- v(A) OR v(B) = 1
- NOT v(A) = 1
From NOT v(A) = 1, we can infer that v(A) = 0. So, the first equation becomes 0 OR v(B) = 1. The only value for v(B) for which this is true is v(B) = 1. And if v(B) = 1, then v B .

So, what we’ve seen is that for all valuations v, if v A B A , then v B . In other words,

A B A B