Tutorial 6. Logical conditionals
Exercise sheet
Boolean conditional
We’ve interpreted the conditional symbol
 using the Booleans NOT
and OR. But we could also have directly defined a Boolean function IF
with the following truth-table:
using the Booleans NOT
and OR. But we could also have directly defined a Boolean function IF
with the following truth-table:
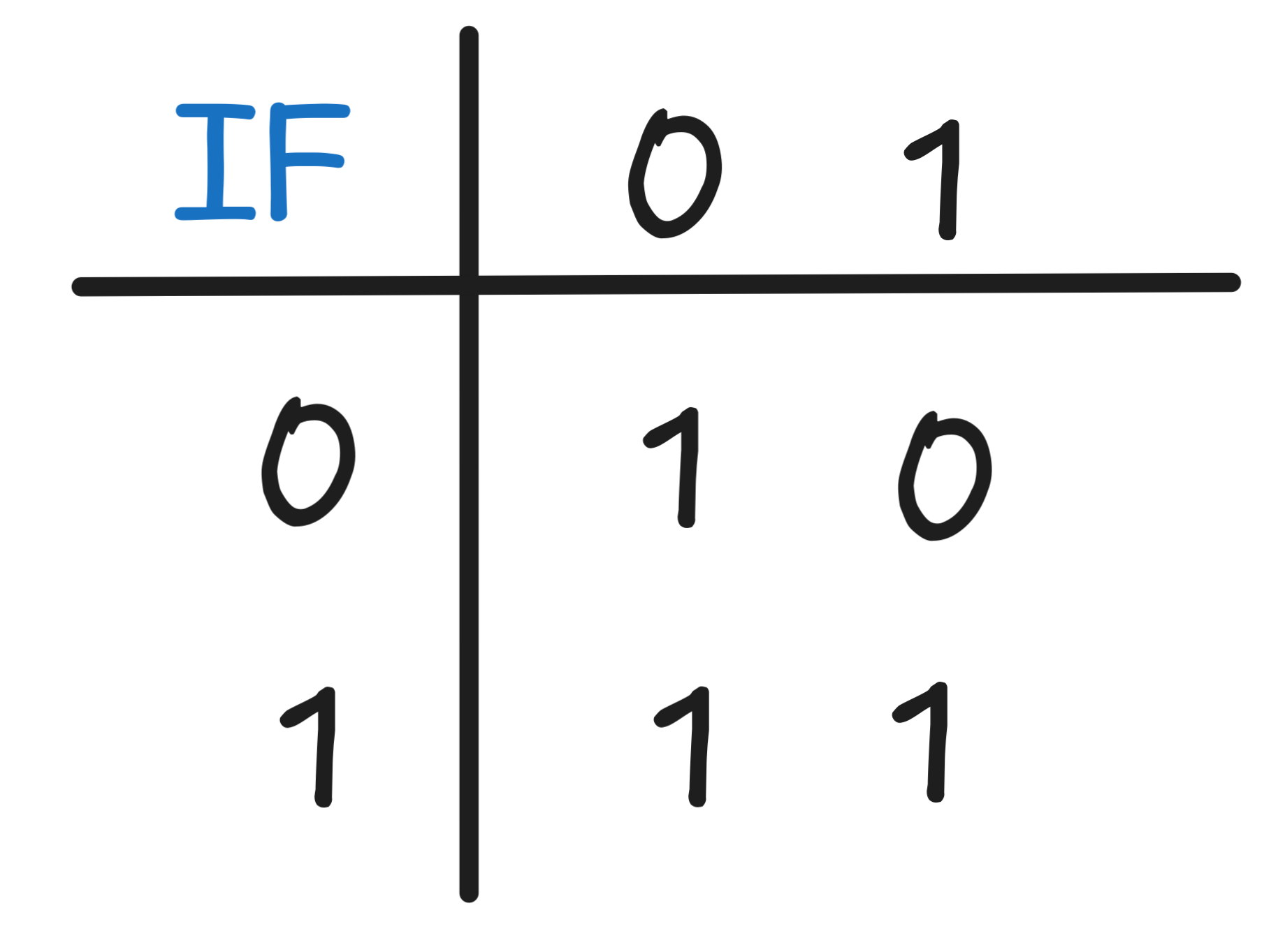
Note that X IF Y is the conditional from the value of X to the value
of Y to make the reading of the Boolean align with its natural reading.
Find a representation of this Boolean function using only NOT and AND. That is find a Boolean expression exp in the two variables X and Y, which contains only the Boolean functions NOT and AND, and which meets the specification that for all values of X and Y, we have:
exp = X IF Y.
Verify your work! That is don’t just provide an expression, but show that for all values of X and Y the above equation holds.
Solution
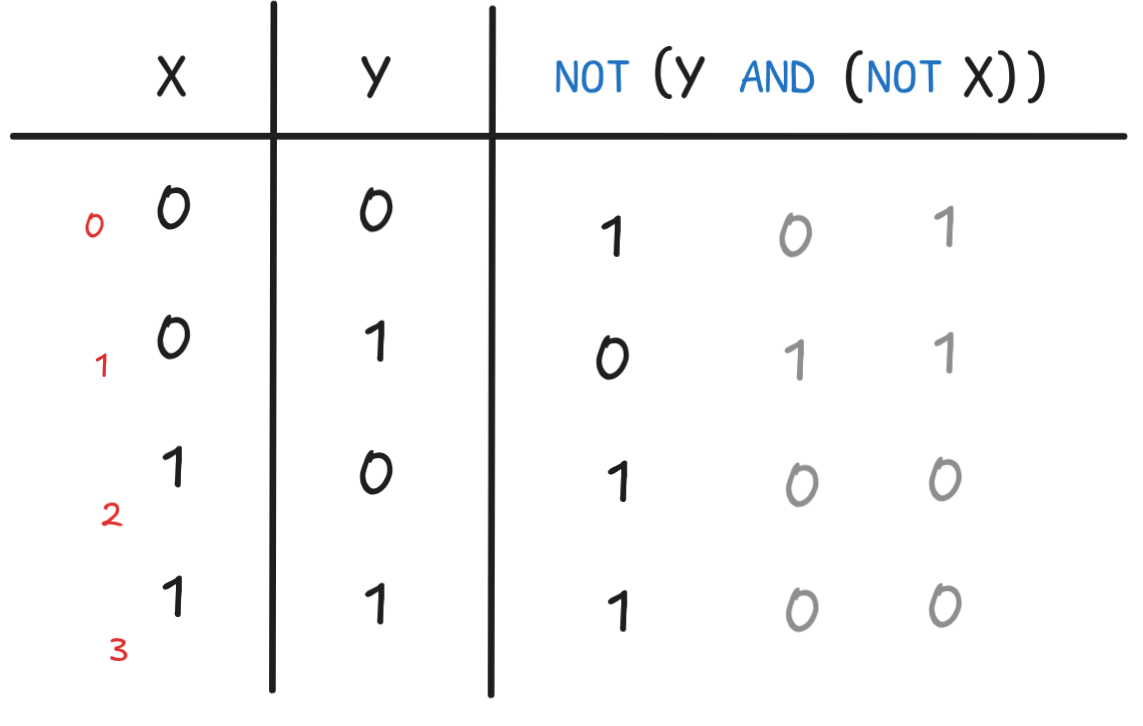
The most straight-forward solution is:
NOT(Y AND (NOT X))
Here’s a truth-table to show that NOT(Y AND (NOT X)) = X IF Y:
Equivalence
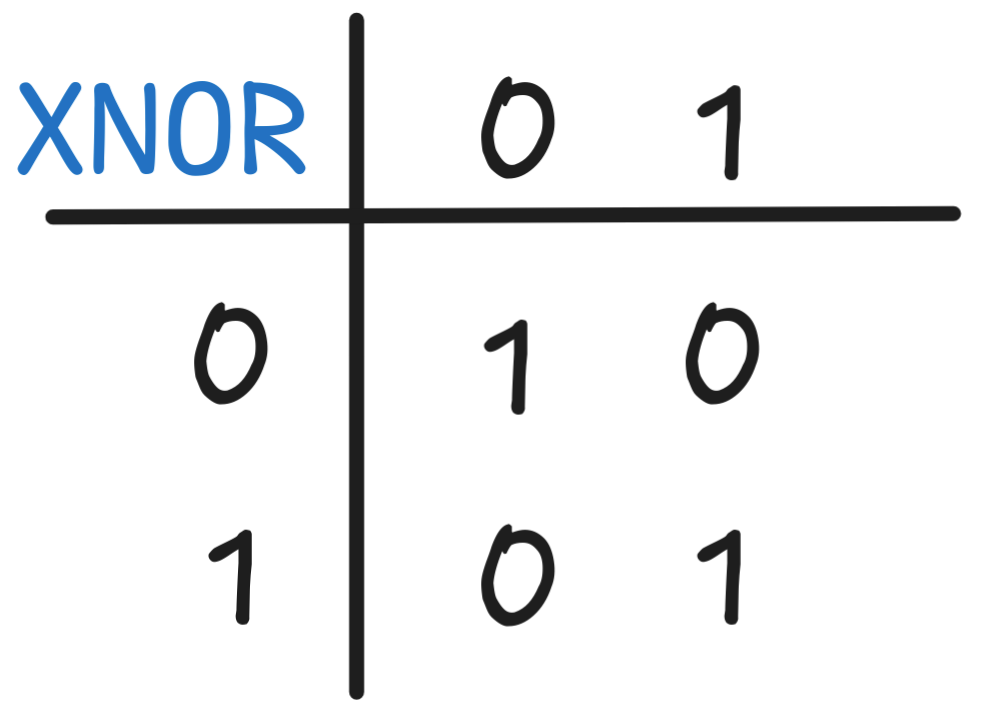
Remember the truth-table for XNOR from the last exercises set:
Find a formula representation of this Boolean truth-function using only the
propositional variables p and q and the connectives
 and
and
 ! That is, find such formula satisfying these constraints, which meets
the assignments v of truth-values to p and q, we have:
! That is, find such formula satisfying these constraints, which meets
the assignments v of truth-values to p and q, we have:
Verify your work! That is don’t just provide a formula, but show that for each assignment the above equation holds.
Solution
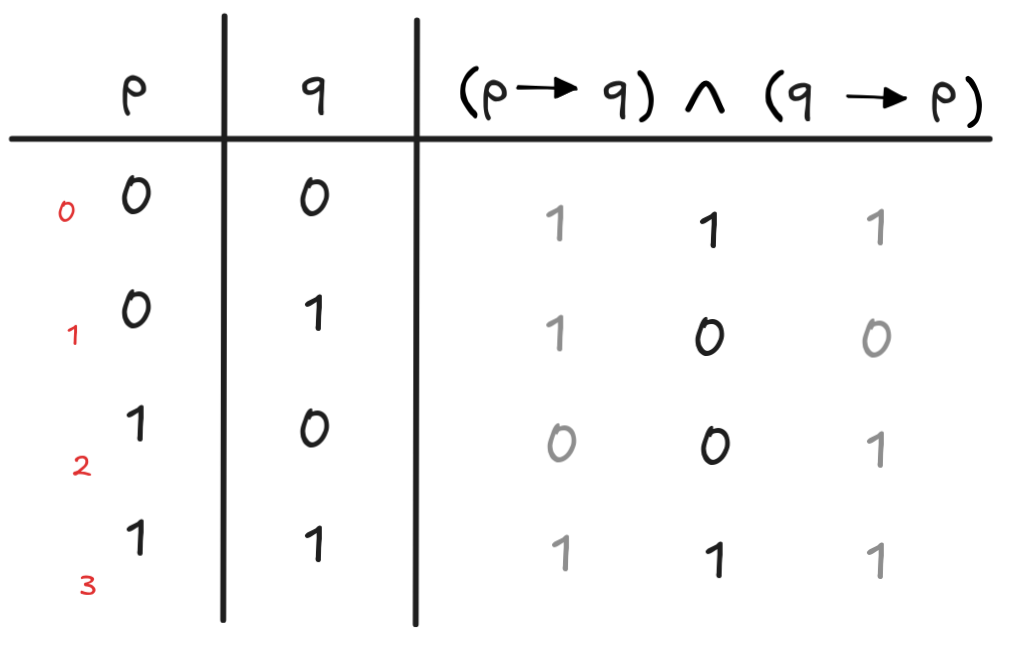
One of the conceptually clearest solutions is the formula:
(p
 q)
q)
 (q
(q
 p)
p)
Here’s a truth-table to verify our work:
Conditional inferences

Check the following conditional inferences for deductive validity using
SAT-solving. You can use truth-tables or resolution, as you prefer.
-
(RAIN
 WIND),
WIND),
 RAIN
RAIN

 WIND
WIND -
(RAIN
 WIND)
WIND)
 (
(
 WIND
WIND

 RAIN)
RAIN) -
(
 RAIN
RAIN
 RAIN)
RAIN)
 RAIN
RAIN -
(RAIN
 ( SUN
( SUN
 RAINBOW))
RAINBOW))
 ((RAIN
((RAIN
 SUN)
SUN)
 RAINBOW)
RAINBOW) -
 (RAIN
(RAIN
 WIND)
WIND)
 RAIN
RAIN
 Document your work carefully, that is explain each step you’re carrying out,
and why the work you did shows that the inference in question is valid or invalid.
Document your work carefully, that is explain each step you’re carrying out,
and why the work you did shows that the inference in question is valid or invalid.
Solution
-
(RAIN
 WIND),
WIND),
 RAIN
RAIN

 WIND. We show this using resolution.
WIND. We show this using resolution.The aim is to show that {(RAIN
 WIND),
WIND),
 RAIN ,
RAIN ,

 WIND } is satisfiable.
WIND } is satisfiable.First, we transform into CNF. The conditional becomes
 RAIN
RAIN
 WIND using r₀, and
WIND using r₀, and

 WIND } becomes WIND using r₁.
WIND } becomes WIND using r₁.This leaves us with the sets
{No resolution is possible, and we can read off a counter-model where v(RAIN) = 0 and v(WIND) = 1. RAIN, WIND } {
RAIN, WIND } {
 RAIN } { WIND }.
RAIN } { WIND }. -
(RAIN
 WIND)
WIND)
 (
(
 WIND
WIND

 RAIN). We show this using resolution.
RAIN). We show this using resolution.The aim is to show that { (RAIN
 WIND),
WIND),
 (
(
 WIND
WIND

 RAIN) } is unsatisfiable.
RAIN) } is unsatisfiable.First, we transform into CNF, beginning by transforming the conditionals using r₀, giving us
 RAIN
RAIN
 WIND
and
WIND
and
 (
(

 WIND
WIND

 RAIN).
RAIN).Applying r₁ and r₃ recursively to the latter, we obtain
 WIND
WIND
 RAIN. This gives us the sets: {.
RAIN. This gives us the sets: {. RAIN, WIND }
{
RAIN, WIND }
{
 WIND } { RAIN }
WIND } { RAIN }We derive the empty set { } in two steps:
-
With {
 RAIN, WIND } and {
RAIN, WIND } and {
 WIND }, we resolve
to {
WIND }, we resolve
to {
 RAIN}.
RAIN}. -
With {
 RAIN} and { RAIN }, we resolve to the empty set {
} proving the unsatisfiability of the set.
RAIN} and { RAIN }, we resolve to the empty set {
} proving the unsatisfiability of the set.
-
-
(
 RAIN
RAIN
 RAIN)
RAIN)
 RAIN. We show this using
truth-tables.
RAIN. We show this using
truth-tables.The aim is to show that {(
 RAIN
RAIN
 RAIN),
RAIN),
 RAIN } is
unsatisfiable. Here’s the truth-table to the effect:
RAIN } is
unsatisfiable. Here’s the truth-table to the effect: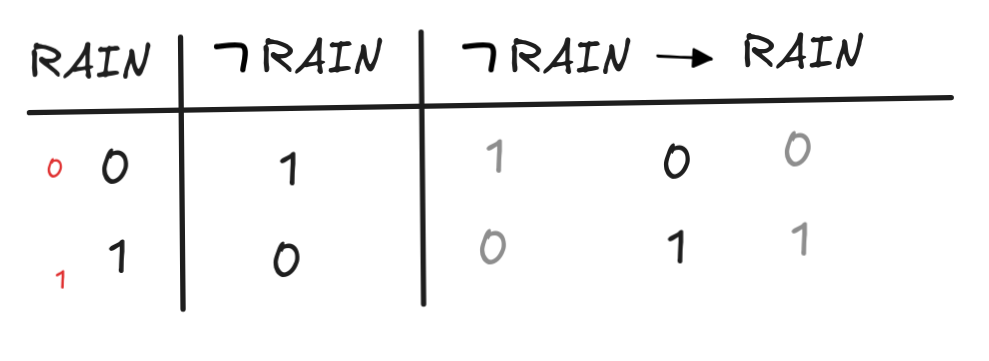
In fact, you can see that
 RAIN
RAIN
 RAIN is equivalent to
RAIN. In logical theory, this is called
Clavius'
Law
.
RAIN is equivalent to
RAIN. In logical theory, this is called
Clavius'
Law
. -
(RAIN
 ( SUN
( SUN
 RAINBOW))
RAINBOW))
 ((RAIN
((RAIN
 SUN)
SUN)
 RAINBOW). We use resolution.
RAINBOW). We use resolution.The task is to show that
{ (RAINis not satisfiable. ( SUN
( SUN
 RAINBOW)),
RAINBOW)),
 ((RAIN
((RAIN
 SUN)
SUN)
 RAINBOW) }
RAINBOW) }First, we trans form to CNF. Recursively applying r₀, we get
from RAIN
RAIN

 SUN
SUN
 RAINBOWRAIN
RAINBOWRAIN ( SUN
( SUN
 RAINBOW).
RAINBOW).For the second formula,
we get ((RAIN
((RAIN
 SUN)
SUN)
 RAINBOW),using r₀ and then
RAINBOW),using r₀ and then (
(
 (RAIN
(RAIN
 SUN)
SUN)
 RAINBOW)using r₂ Finally, r₁ give us:
RAINBOW)using r₂ Finally, r₁ give us:
 (RAIN
(RAIN
 SUN)
SUN)

 RAINBOW)RAIN
RAINBOW)RAIN SUN
SUN

 RAINBOW
RAINBOWThis give us the sets:
{ RAIN,
RAIN,
 SUN, RAINBOW } { RAIN } { SUN } {
SUN, RAINBOW } { RAIN } { SUN } {
 RAINBOW }
RAINBOW }The derivation of { } using resolution is a simple, three-step affair:
-
{
 RAIN,
RAIN,
 SUN, RAINBOW} and { RAIN } give us {
SUN, RAINBOW} and { RAIN } give us {
 SUN, RAINBOW}.
SUN, RAINBOW}. -
{
 SUN, RAINBOW} and { SUN } give us { RAINBOW }
SUN, RAINBOW} and { SUN } give us { RAINBOW } -
{ RAINBOW } and {
 RAINBOW } give us { }.
RAINBOW } give us { }.
-
-
 (RAIN
(RAIN
 WIND)
WIND)
 RAIN, which we show using
truth-tables.
RAIN, which we show using
truth-tables.The aim is to show that {
 (RAIN
(RAIN
 WIND),
WIND),
 RAIN } is unsatisfiable.
RAIN } is unsatisfiable.Here’s the table:
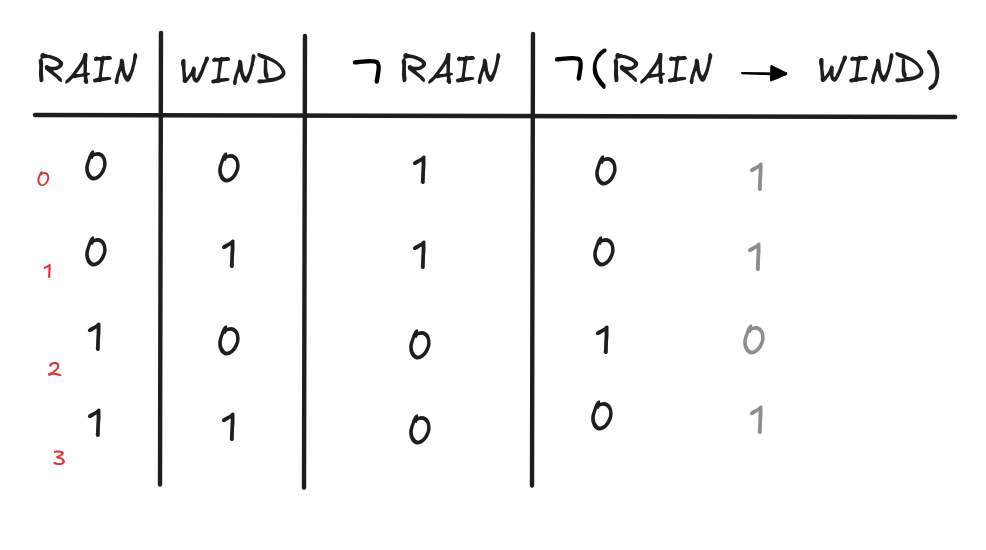
Since there’s no row where both
 (RAIN
(RAIN
 WIND) and
WIND) and
 RAIN are
RAIN are 1, the set is unsatisfiable.
Valid inference and conditionals
There’s a deep connection between deductively valid inference in Boolean logic and material conditionals, which is given by the following important equivalence:
 C if and only if not-SAT{
C if and only if not-SAT{
 ((P₁
((P₁
 P₂
P₂
 … )
… )
 C)}
C)}-
A logical formula A is called a logical truth iff for all assignments v of truth-values to its propositional variables, the formula is true, i.e. v(A) = 1. Verify that the simple formula
(RAINis a logical truth in this sense.
 RAIN)
RAIN) -
Rephrase the right-hand side of above equivalence in terms of the logical truth rather than unsatisfiability.
-
Give an argument that the above equivalence is true.
Hint: To do so, you need to use the general form of the reduction of valid inference to unsatisfiability, which we’ve discussed in the lecture
P₁, P₂, …Think about what the latter condition means for the truth of the corresponding conditional. C if and only if not-SAT { P₁, P₂, … ,
C if and only if not-SAT { P₁, P₂, … ,
 C }
C }
Solution
-
We could do a truth-table, but let’s do a step-by step calculation, instead, where we go through the two possibilities: v(RAIN) = 1 or v(RAIN) = 0:
- If v(RAIN) = 1, then v(RAIN

 RAIN) = v(RAIN) OR
v(
RAIN) = v(RAIN) OR
v(
 RAIN)= …
RAIN)= …
... = v(RAIN) OR (NOT v(RAIN)) = 1 OR (NOT 1) = 1 OR 0 = 1.- If v(RAIN) = 0, then v(RAIN

 RAIN) = v(RAIN) OR
v(
RAIN) = v(RAIN) OR
v(
 RAIN)= …
RAIN)= …
... = v(RAIN) OR (NOT v(RAIN)) = 0 OR (NOT 0) = 0 OR 1 = 1.So, in all possible cases, we have v(RAIN

 RAIN) = 1.
RAIN) = 1. - If v(RAIN) = 1, then
-
First, note that not-SAT{
 ((P₁
((P₁
 P₂
P₂
 … )
… )
 C)} means that the formula
C)} means that the formula
 ((P₁
((P₁
 P₂
P₂
 … )
… )
 C) is
unsatisfiable, meaning it has value
C) is
unsatisfiable, meaning it has value 0under every valuation. But the formula starts with a and so v(But if we know that this expression evaluates to
and so v(But if we know that this expression evaluates to ((P₁
((P₁
 P₂
P₂
 … )
… )
 C)) = NOT v((P₁
C)) = NOT v((P₁
 P₂
P₂
 …)
…)
 C)
C)0under each valuation, this means that v((P₁ P₂
P₂
 …
)
…
)
 C) = 1 under each valuation. In other words, (P₁is a logical truth. This gives us an alternative criterion for valid inference according to which:
C) = 1 under each valuation. In other words, (P₁is a logical truth. This gives us an alternative criterion for valid inference according to which: P₂
P₂
 … )
… )
 CP₁, P₂, …This criterion shows the particularly deep connection between valid inference and conditionals.
CP₁, P₂, …This criterion shows the particularly deep connection between valid inference and conditionals. C if and only if (P₁
C if and only if (P₁
 P₂
P₂
 … )
… )
 C is a
logical truth
C is a
logical truth -
This is the hardest part and more advanced logical reasoning. One way to proceed is to start from the known criterion that
P₁, P₂, …Let’s think about not-SAT { P₁, P₂, … , C if and only if not-SAT {
P₁, P₂, … ,
C if and only if not-SAT {
P₁, P₂, … ,
 C }.
C }. C }. This means that for
each valuation, either v(P₁) = 0, v(P₂) = 0, … , or v(
C }. This means that for
each valuation, either v(P₁) = 0, v(P₂) = 0, … , or v(
 C) = 0.
Using transformations, we can see that (P₁
C) = 0.
Using transformations, we can see that (P₁
 P₂
P₂
 …)
…)
 C is equivalent to
C is equivalent to
 P₁
P₁

 P₂
P₂
 …
…
 C. That is: v((P₁Using the recursive rules, we get:
C. That is: v((P₁Using the recursive rules, we get: P₂
P₂
 … )
… )
 C) = v(
C) = v(
 P₁
P₁

 P₂
P₂
 …
…
 C).v(But if v(P₁) = 0, then
C).v(But if v(P₁) = 0, then P₁
P₁

 P₂
P₂
 …
…
 C) = (NOT v(P₁)) OR (NOT v(P₂)) OR … OR v(C)(NOT v(P₁)) OR (NOT v(P₂)) OR … OR v(C) = …… = (NOT 0) OR (NOT v(P₂)) OR … OR v(C) = …… = 1 OR OR (NOT v(P₂)) OR … OR v(C) = 1Similarly, if v(P₂) = 0, then(NOT v(P₁)) OR (NOT v(P₂)) OR … OR v(C) = …… = (NOT v(P₂)) OR (NOT 0) OR … OR v(C) = …… = 1 OR OR (NOT v(P₂)) OR … OR v(C) = 1And so on. Finally, if v(
C) = (NOT v(P₁)) OR (NOT v(P₂)) OR … OR v(C)(NOT v(P₁)) OR (NOT v(P₂)) OR … OR v(C) = …… = (NOT 0) OR (NOT v(P₂)) OR … OR v(C) = …… = 1 OR OR (NOT v(P₂)) OR … OR v(C) = 1Similarly, if v(P₂) = 0, then(NOT v(P₁)) OR (NOT v(P₂)) OR … OR v(C) = …… = (NOT v(P₂)) OR (NOT 0) OR … OR v(C) = …… = 1 OR OR (NOT v(P₂)) OR … OR v(C) = 1And so on. Finally, if v( C) = 0, then v(C) = 1 and so (NOT v(P₁)) OR (NOT v(P₂)) OR … OR v(C) = …… = (NOT v(P₁)) OR (NOT v(P₂)) OR … OR 1 = 1.Since these are all the possibilities if not-SAT { P₁, P₂, … ,
C) = 0, then v(C) = 1 and so (NOT v(P₁)) OR (NOT v(P₂)) OR … OR v(C) = …… = (NOT v(P₁)) OR (NOT v(P₂)) OR … OR 1 = 1.Since these are all the possibilities if not-SAT { P₁, P₂, … , C }, we know
that v((P₁
C }, we know
that v((P₁
 P₂
P₂
 … )
… )
 C) = 1 for all valuations.
By similar reasoning, we can see that if v((P₁
C) = 1 for all valuations.
By similar reasoning, we can see that if v((P₁
 P₂
P₂
 … )
… )
 C) = 1 for all valuations, then not-SAT { P₁, P₂, … ,
C) = 1 for all valuations, then not-SAT { P₁, P₂, … ,
 C } since
otherwise, there would be a valuation v with v((P₁
C } since
otherwise, there would be a valuation v with v((P₁
 P₂
P₂
 … )
… )
 C) = 0.
C) = 0.
Chaining
Consider the following KB:
- RAIN
 CLOUDS
CLOUDS - (CLOUDS
 SNOW)
SNOW)
 STORM
STORM - RAIN
 PUDDLES
PUDDLES - PUDDLES
 HUMID
HUMID - HUMID
 CLOUDS
CLOUDS - SUN
 DRY
DRY - (WIND
 SNOW)
SNOW)
 DRIFTING
DRIFTING
We add to this KB the following two facts:
-
Run the forward-chaining and the backward-chaining algorithm to show that we can derive STORM from the KB. That is, describe the steps you’d take for each algorithm one-by-one, and why at some point you hit the termination condition.
-
Use the example to illustrate how forward-chaining can find shorter derivations than backward-chaining.
-
Use both forward and backward-chaining to show that we can’t derive DRIFTING from the KB using the facts. Does one algorithm outperform the other?
Solution
-
Our goal is derive STORM. The facts are RAIN and SNOW. First, we use forward chaining:
-
So, in the first iteration, we run through all the conditionals and see if we can derive anything from those facts using genMP. We come across the two conditionals RAIN
 CLOUDS and RAIN
CLOUDS and RAIN
 PUDDLES. We derive CLOUDS and PUDDLES and add them two our facts. But our goal is not reached.
PUDDLES. We derive CLOUDS and PUDDLES and add them two our facts. But our goal is not reached. -
So, in the second step, the facts are RAIN, SNOW, CLOUDS, and PUDDLES. Again, we check the conditionals for possible MP applications and find (CLOUDS
 SNOW)
SNOW)
 STORM
and PUDDLES
STORM
and PUDDLES
 HUMID. We derive both STORM and HUMID. Our
goal is reached and we terminate the search.
HUMID. We derive both STORM and HUMID. Our
goal is reached and we terminate the search.
Next, we use backward chaining:
-
Our goal is STORM, so we inspect the conditionals until we find one that contains STORM as the consequent. We find (CLOUDS
 SNOW)
SNOW)
 STORM. We recognize that SNOW is
already among our facts, so we replace the goal STORM temporarily
with CLOUDS. Since we still have goals, we continue.
STORM. We recognize that SNOW is
already among our facts, so we replace the goal STORM temporarily
with CLOUDS. Since we still have goals, we continue. -
We inspect the rules for one with CLOUDS in the consequent and find RAIN
 CLOUDS. Since RAIN is among our facts, we
have no goals left and terminate the search.
CLOUDS. Since RAIN is among our facts, we
have no goals left and terminate the search.
Both algorithms lead to the same result and, in fact, give the same derivation.
-
-
In the forward-chaining algorithm, there were no choices involved and we simply looked through all chainings of MP by length until we found one. Since we went through the derivations by length starting with the shortest derivations, we were guaranteed to come across the shortest derivation first (if there is one).
For backward-chaining, finding this particular derivation depended on the order in which we looked through the rules. If, for some implementation reason, we would have first come across HUMID
 CLOUDS in the second step, we would have added HUMID to our goals rather than RAIN. Then, we’d have continued two more iterations going through PUDDLES
CLOUDS in the second step, we would have added HUMID to our goals rather than RAIN. Then, we’d have continued two more iterations going through PUDDLES
 HUMID and RAIN
HUMID and RAIN
 PUDDLES until we hit a known fact. This would have lead to a much longer derivation. This means that with backward-chaining, whether we come across the shortest derivation first, highly depends on external factors, like the ordering of the conditionals in our KB.
PUDDLES until we hit a known fact. This would have lead to a much longer derivation. This means that with backward-chaining, whether we come across the shortest derivation first, highly depends on external factors, like the ordering of the conditionals in our KB. -
To test this with forward-chaining, we go through all possible derivations. We’ve described the first two steps above, which gave us STORM and PUDDLES. Continuing further, we derive HUMID using PUDDLES and PUDDLES
 HUMID and then CLOUDS from HUMID and HUMID
HUMID and then CLOUDS from HUMID and HUMID
 CLOUDS. At this point, we have RAIN, SNOW, STORM, PUDDLES, HUMID, and CLOUDS among our facts and can’t apply genMP anymore. Since DRIFTING isn’t among these facts, we conclude it can’t be derived.
CLOUDS. At this point, we have RAIN, SNOW, STORM, PUDDLES, HUMID, and CLOUDS among our facts and can’t apply genMP anymore. Since DRIFTING isn’t among these facts, we conclude it can’t be derived.With backward-chaining, instead, we check for conditionals involving DRIFTING in the consequent and only find (WIND
 SNOW
SNOW
 DRIFTING). This adds WIND to our goals, since SNOW is already a fact. In the second iteration, we can’t find a conditional that has WIND in the consequent, so we terminate our search and conclude that DRIFTING can’t be derived.
DRIFTING). This adds WIND to our goals, since SNOW is already a fact. In the second iteration, we can’t find a conditional that has WIND in the consequent, so we terminate our search and conclude that DRIFTING can’t be derived.Here, backward-chaining was way more efficient. This is because forward-chaining needs to go through all possible derivations to determine whether there is one, which derives our desired goal. Backward-chaining is more “surgical” in that it only looks through promising candidates and terminates earlier because there are none.
Planning
We’ve made things a more difficult for IA by introducing a third block into the puzzle:
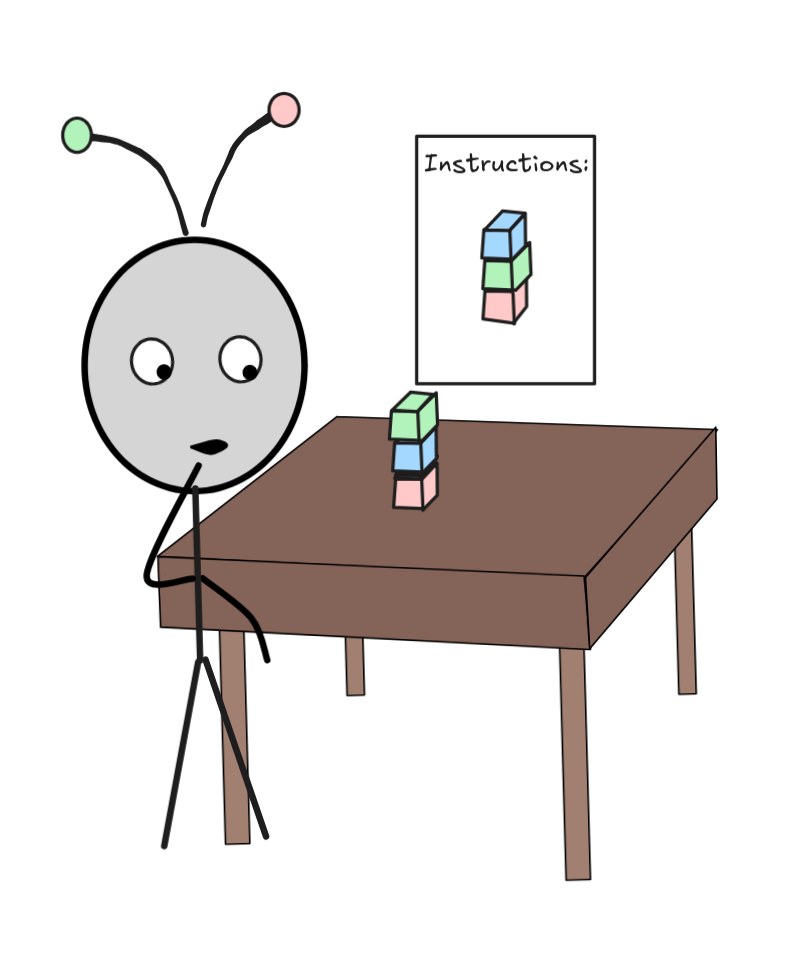 le
Adjust our planning solution to accommodate the more complicated setup. That is:
le
Adjust our planning solution to accommodate the more complicated setup. That is:
-
Determine how we need to adjust the language to accommodate the third block.
-
Which rules do we need to add to our a KB to accommodate the third block.
-
Represent the initial setup state and the goal state in the language.
-
Find a model that satisfies the KB, as well as the setup and goal state. Then read off a course o action. You don’t need to do this formally—using resolution or chaining—but just find such a model using human intelligence.
Solution
-
On the language side, we need to add all the instances of the schemata On(X,Y,t), Stack(X,Y,t), Unstack(X,Y,t) for X,Y
 {R,G,B} and
t
{R,G,B} and
t
 {0, 1, 2, …}, where the statements involving B represent the
facts involving the new blue block.
{0, 1, 2, …}, where the statements involving B represent the
facts involving the new blue block. -
In terms of the rules, all previous rules can remain the same just involving B, so
 On(X,X) for X
On(X,X) for X
 {R,B,G}, and so on. We do need
to add principles that exclude new weird configurations that are logically
possible, such as On(R,G,t)
{R,B,G}, and so on. We do need
to add principles that exclude new weird configurations that are logically
possible, such as On(R,G,t)
 On(G, B,t)
On(G, B,t)
 On(B,R,t) for
some time t. On previous rules only excluded 2-step loops, like On(R,G,t)
On(B,R,t) for
some time t. On previous rules only excluded 2-step loops, like On(R,G,t)
 On(G,R,t), but not 3-step loops like the one above. We could just add the schema:On(X,Y,t)
On(G,R,t), but not 3-step loops like the one above. We could just add the schema:On(X,Y,t) On(Y, Z,t)
On(Y, Z,t)

 On(Z,X,t)
On(Z,X,t)There is one kind of rule that we would need to include concerning the actions that wasn’t relevant before. Now that there are three blocks, we should watch out that we can only unstack one block from another if there’s no other block on the top. That is, we need to postulate,
Unstack(R,G,t)
 On(B,R,t)Unstack(R,B,t)
On(B,R,t)Unstack(R,B,t)
 On(G,R,t)Unstack(G,B,t)
On(G,R,t)Unstack(G,B,t)
 On(R,G,t)...
On(R,G,t)...Similarly, we can only stack one block on top of another, if there’s no other block on top yet:
Stack(R,G,t)
 On(B,G,t)Stack(R,B,t)
On(B,G,t)Stack(R,B,t)
 On(G,B,t)...
On(G,B,t)...The persistence conditions remain the same.
-
Our set-up, then is:
On(G,B,0) On(B,R,0)
On(B,R,0)And the goal state is:
On(B,G,t) On(G,R,t)
On(G,R,t)for some suitable t. As you can see, we can achieve this for t=4 (five steps).
-
Here’s one strategy. I only note the relevant formulas, all unnamed formulas are assumed to be false:
-
First step:
-
State: On(G,B,0), On(B,R,0)
-
Action: Unstack(G,B,0) (possible because neither On(R,G,0) nor On(B,G,0))
-
-
Second step:
-
State:
 On(G,B,1), On(B,R,1)
On(G,B,1), On(B,R,1) -
Action: Unstack(B,R,1) (possible because now
 On(G,B,1))
On(G,B,1))
-
-
Third step:
-
State:
 On(G,B,2),
On(G,B,2),
 On(B,R,2)
On(B,R,2) -
Action: Stack(B,R,2) (possible because at this point neither On(G,R,2) nor On(B,R,2))
-
-
Fourth step:
-
State: On(B,R,3),
 On(B,R,3)
On(B,R,3) -
Action: Stack(G,B,3)
-
-
Fifth step:
- State: On(G,B,4),
 On(B,R,4)
On(B,R,4)
- State: On(G,B,4),
-
You can straight-forwardly check that all conditions are satisfied.
Discussion
Check out the Wason selection task on Wikipedia.
Some researchers have argued that the experiment shows that people don’t reason with the material conditional in this case. Do you agree? Why?