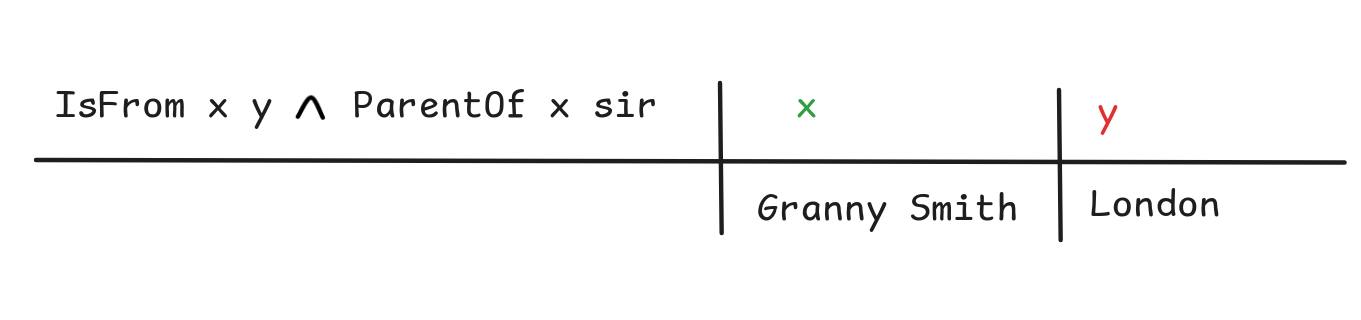logicalmethods.ai

Tutorial 8. FOL

Exercise sheet

Decoding FOL

Paraphrase the following FOL formulas in natural language:

x (FatherOf x brotherOf jimmy FatherOf x jimmy)
x ( Fish x y (Fish y BiggerThan y x ))
x SiblingOf jimmy x x( SiblingOf jimmy x y ( Sibling x y YoungerThan y x))
x y (Thief x Thief y x = y)

Solution

There is a person who’s the father of Jimmy’s brother but not Jimmy’s father.
For each fish, there’s a bigger fish.
If Jimmy has a sibling at all, then one of Jimmy’s siblings is older than all of their siblings.
There are at least two different thieves.

Knowledge Engineering in FOL

Knowledge engineering is the complex process of developing a framework in which to encode knowledge about a specific domain. There are different approaches to this problem, but here we’ll try out an FOL-based approach.

The problem we’re tackling is to represent information about a given setup using FOL formulas. The first step on the approach is to decide on a suitable vocabulary. Since we’re working with FOL languages, this means that we need to pick suitable constants, function symbols, and predicates to represent the information. Picking the right vocabulary is crucial for success when dealing with a knowledge engineering problem: choosing the wrong vocabulary can make representations clunky and hard to work with, even if—in some sense—still correct.

Picking the right language is closely related to finding a suitable ontology for the problem. That is, we need to say which objects exist in the information, which functions and properties are at play. We also need to answer questions like whether we can reduce some properties to others do have a simpler language. For example, should we have a separate predicate for Uncle² or should we define it using Male¹, Sibling², and Parent², where rather than Uncle x y we use:


Male y 

 
 
 
z (Parent z x 

 Sibling y z)

Uncle x y is much simpler, but the previous formula contains more information. There is a trade-off that needs to be weighed carefully for every proposed knowledge engineering solution.

The second step in FOL knowledge engineering is to take the given information and to encode it with FOL formulas. Here, the main challenge is adequacy: we need to find formulas whose FOL truth-conditions resemble the given information as closely as possible, while remaining within the confines of FOL.

For a concrete knowledge engineering problem, lets consider the following marketing information about IA provided by its developer:

Our IA is the top-of-the-line AI system from AI-Labs. It is a hybrid system that has both symbolic and sub-symbolic sub-routines. This means that IA is both capable of carrying out all traditional reasoning tasks, such as natural deduction or SAT solving, as well as different learned tasks, such as image and voice recognition. This is in contrast to its predecessor model KnowIt∀, which only had symbolic routines and could only carry out reasoning tasks. It also makes IA superior to the competition’s model, DeepL, which is a purely sub-symbolic AI-system and while able to carry out all learned tasks, can only carry out some simple reasoning tasks.

Devise a suitable FOL language for encoding the information about the three AI-systems. Justify your design choices.
Encode as much information as possible from the advert as FOL formulas. Is there information you chose not to include? If so, why?
It’s a bad idea to include a function symbol makerOf in this language. Explain why.

Solution

There are different ways of doing this. One way to go is this:
- Constants: ∀I, KnowIt∀, DeepL, image_recognition, voice_recognition, natural_deduction, sat_solving
- Predicates: IsSymbolic², IsSubSymbolic², IsReasoningTask¹, IsLearnedTask¹, IsCapableOf²
This language has names for certain tasks, like voice recognition or natural deduction, which means that it includes them in its ontology. This means, for example, that in models of that language these tasks will be objects in the domain. An alternative approach would be to include corresponding properties, like IsCapableOfNaturalDeduction¹, which however leads to a proliferation of predicates.
At a minimum, the following information should be included:
- IsSymbolic ∀I IsSubSymbolic ∀I
- x (IsReasoningTask x IsCapableOf ∀I x)
- x (IsLearnedTask x IsCapableOf ∀I x)
- IsCapableOf ∀I natural_deduction, IsCapableOf ∀I sat_solving
- IsCapableOf ∀I voice_recognition, IsCapableOf ∀I image_recognition
- IsSymbolic KnowIt∀ IsSubSymbolic KnowIt∀
- x (IsCabaleOf KnowIt∀ x IsReasoningTask x)
- IsSymbolic DeepL IsSubSymbolic DeepL
- x (IsLearnedTask x IsCapableOf ∀I x)
- x (IsReasoningTask x IsCapableOf ∀I x)
Implied but not explicitly stated is: x (IsReasoningTask x IsCapableOf ∀I x)
We might add a constant ai_labs and a predicate IsMakerOf² to the language to say that:
- IsMakerOf ai_labs ∀I
The alternative of adding a function symbol makerOf and writing makerOf ∀I = ai_labs is a bad idea since then we’d have to account for the meaning of terms like makerOf ai_labs, which have unclear meaning.

Knowledge Representation with FOL Models

For this exercise, we are working with an FOL language with the following vocabulary:

Constants: jimmy, linus, sir, sir,lady, gran, ny, london, soccer
Predicates: Loves², IsFrom², ParentOf², LivesIn²

Now consider the following facts about our protagonist, little Jimmy:

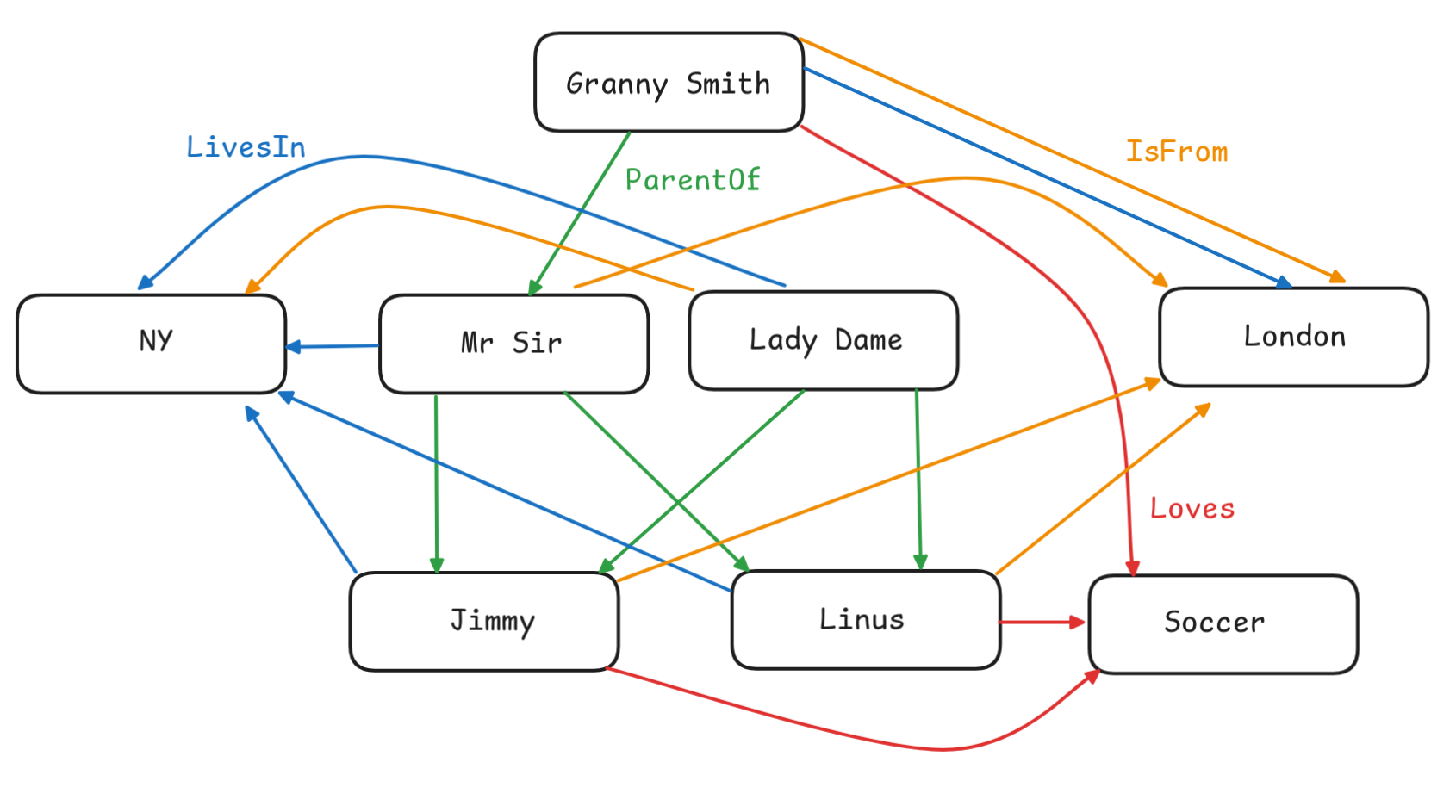
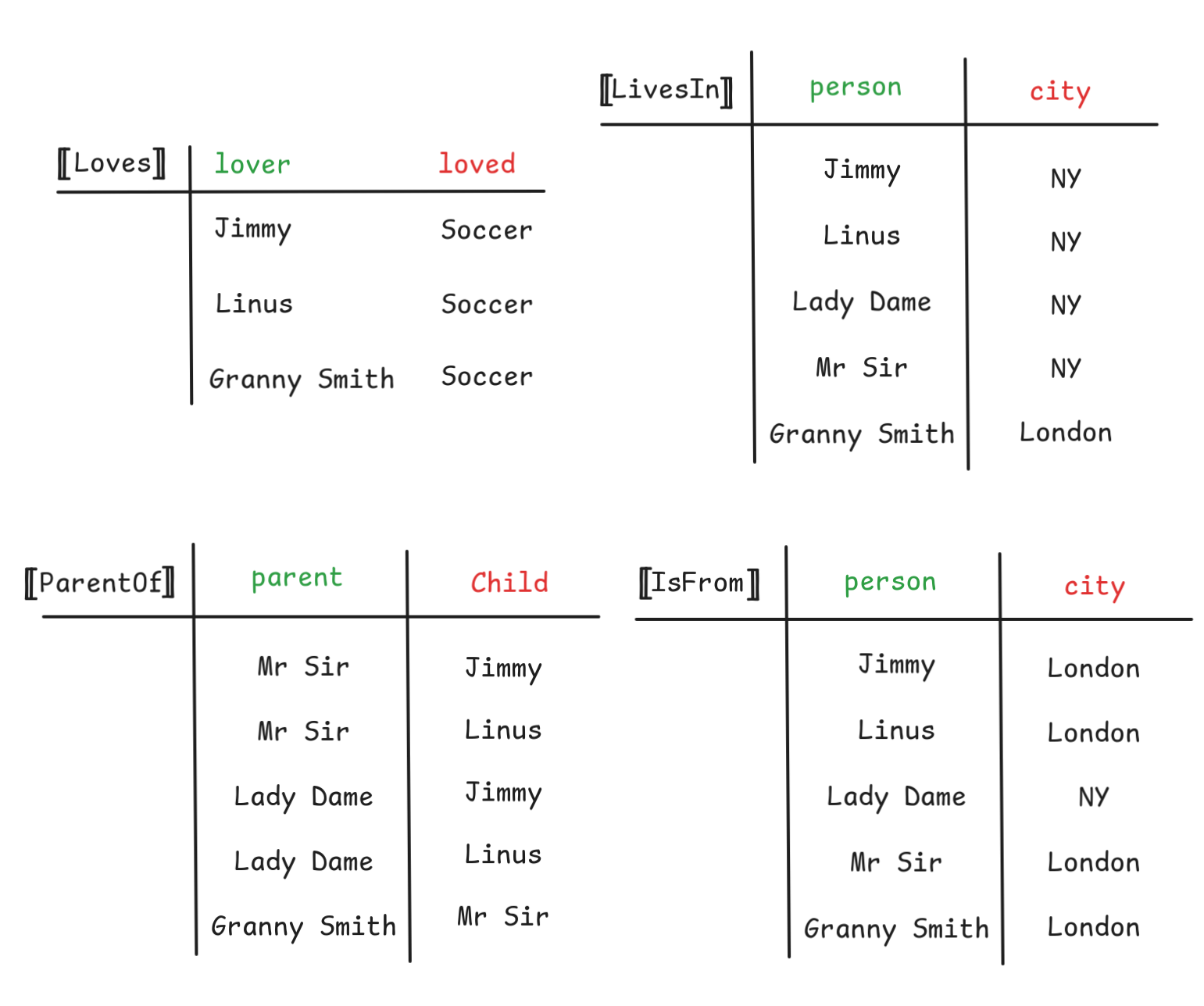
Little Jimmy and his brother, Linus, are the children of Mr Sir and Lady Dame. They family lives in New York, where Lady Dame is from. But both Jimmy and his brother were born in London, where their father is from. The children’s paternal grandmother is Granny Smith, who still lives in London, where she was born. The children and their grandmother love soccer, unlike their parents.

Represent the information as a FOL model. Specify the model in set-theoretic terms, as a knowledge graph, and in table form. Make sure to include the information about which constant denotes which object.
Go to https://www.db-fiddle.com/ and, taking the code from the textbook as a template, create a SQL database that contains the information about the model. Make sure to select SQLite v3.46 on the top left for the language, otherwise the code won’t run. Verify your code by running a query that prints all tables.
In logic, there is the concept of a diagram , which is, essentially, the idea of collecting all the true atomic sentences and true negations of atomic sentences in the model. The positive diagram is the set of only the true atomic sentences, without the true negated ones. Determine the positive diagram of the model we’ve just described. Is this essentially different from any of the other methods of representing the model?

Solution

Here are three representations of the model:
Here’s a db-fiddle with the corresponding tables.
It’s not really different from any of the previous methods. Here’s what we get:
- Loves jimmy soccer
- Loves linus soccer
- Loves gran soccer
- IsFrom jimmy london
- IsFrom linus london
- IsFrom sir london
- IsFrom lady ny
- IsFrom gran london
- LivesIn jimmy ny
- LivesIn linus ny
- LivesIn sr ny
- LivesIn lady ny
- LivesIn gran london
- ParentOf sir jimmy
- ParentOf sir linus
- ParentOf lady jimmy
- ParentOf lady linus
- ParentOf gran sir
The full atomic diagram, however, is much larger, since there are plenty of false atoms, like ParentOf soccer ny, so their negations are all true, including ParentOf soccer ny.

Denotation

Suppose that we’re working with an FOL language that has the single constant null, as well as the function symbols succ¹ and prod².

Consider the model whose domain D = { 0, 1, 2, … } is the set of natural numbers and where:

null = 0
succ is defined by the equation succ (n) = n + 1 for all n { 0 , 1, 2, … }.
prod is defined by the equation prod (n,m) = n × m for all n, m { 0 , 1, 2, … }.

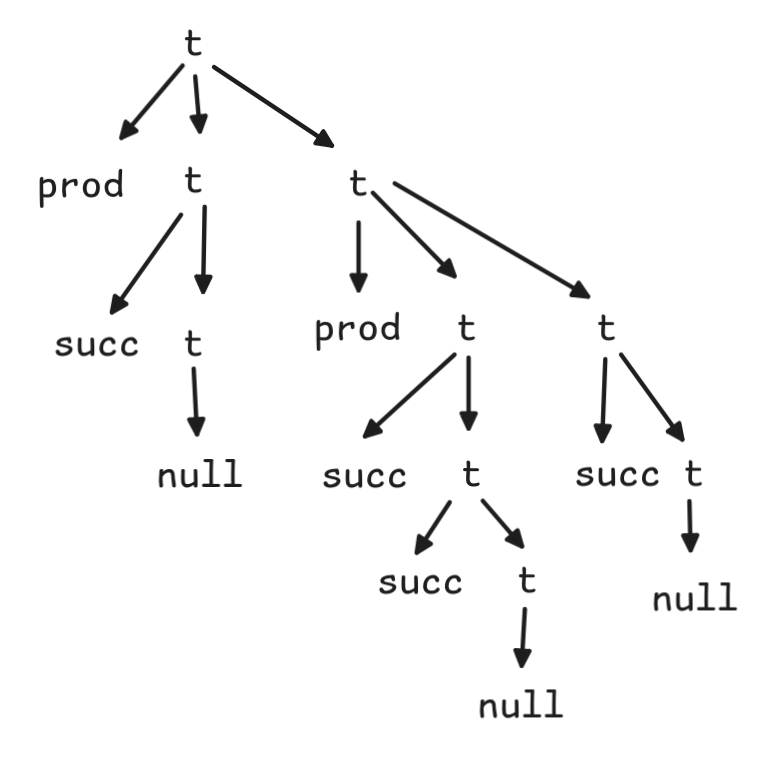
In this model, determine:




 prod succ null  prod succ succ null succ null

For this purpose:

Parse the expression according to the grammar for FOL terms.
Recursively calculate the values of each term, following the terms parsing tree.

Solution

Here’s the parse tree:
Here’s the calculation:
- null = 0
- suc null = suc ( null ) = 0 + 1 = 1
- succ suc null = suc ( succ null ) = 1 + 1 = 2
- prod succ suc null succ null = prod ( succ succ null , succ null ) = 2 x 1 = 2
- prod succ null prod succ suc null succ null = prod ( succ null , prod succ suc null succ null ) = 1 x 2 = 2

Satisfaction

In the model you’ve characterized in exercise 3, determine the extensions of the following open formulas. Give them in table form:

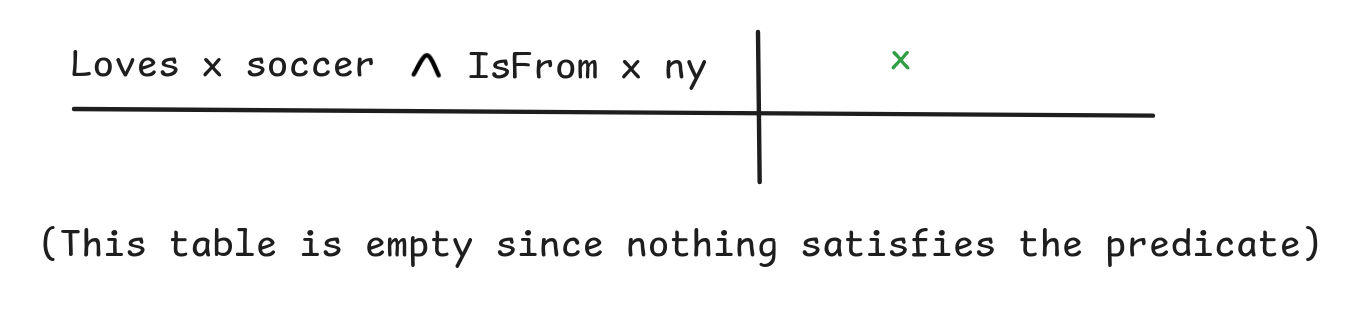
Loves x soccer IsFrom x ny
IsFrom x y ParentOf x sir
y ParentOf y x z ParentOf z y
IsFrom x y LivesIn x y

Solution

SQL Queries

We’ve mentioned that there is a one-to-one correspondence between SQL queries. In this exercise, we’ll explore this connection a bit more.

We return to our country DB from the textbook. You can open it again under db-fiddle .

I should preface this that what we’re doing here is not great SQL practice. We’re writing code that might seem unnatural in SQL and there certainly are better ways to code the queries. The point here is to get the idea of the correspondence across and then worry about learning to code “clean” SQL later (if you want to).

So: SQL is a rich and powerful language of domain-specific languages, and there are much easier ways to make some of these queries.

With this disclaimer out of the way, the starting point for our discussion of the relation between DB queries and open FOL formulas was the observation the SQL query

1
2
3


SELECT country
FROM LocatedIn
WHERE continent = 'Europe';

directly corresponds to the open formula:


LocatedIn x Europe

This correspondence consists in the fact that the table returned by the query is precisely the extension of the formula. To begin with, let’s see if you can formula queries that correspond to other atoms:

Write SQL queries that correspond to to the following atomic open formulas:
- LanguageOf UnitedStates x
- LocatedIn Japan x
- LocatedIn x x

Verify your results using the df-fiddle.

We form complex formulas using the logical operators. These syntactic operations are mirrored by operations on the queries.

Let’s talk about the negation operator first. To negate our atomic query for LocatedIn(x,Europe), we’d use the WHERE NOT EXISTS sub-query, such that

1
2
3


SELECT country
FROM LocatedIn
WHERE continent = 'Europe';

becomes

1
2
3
4
5
6
7
8


SELECT country
FROM CapitalOf
WHERE NOT EXISTS (
  SELECT *
  FROM LocatedIn
  WHERE LocatedIn.country = CapitalOf.country
    AND continent = 'Europe'
);

So, the idea is that we can look for the countries from the CapitalOf table, for which the query corresponding to our unnegated query doesn’t return any value. Note that this assumes that all countries occur in the CapitalOf and in the LocatedIn table. If that’s not the case, we’d need a domain table, but that’s another story.

To test the understanding of this:

Write SQL queries that correspond to to the following negations:
- LanguageOf UnitedStates x
- LocatedIn Japan x
- LocatedIn x x

To conclude our little journey into queries as FOL formulas, let’s talk about conjunction. One approach to form the conjunction is to make sub-queries for each conjunct as follows:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


SELECT country
FROM CapitalOf AS c
WHERE EXISTS (
  SELECT *
  FROM LocatedIn
  WHERE LocatedIn.country = c.country
    AND continent = 'Europe'
)
AND EXISTS (
  SELECT *
  FROM CapitalOf
  WHERE CapitalOf.country = c.country
    AND capital = 'Amsterdam'
);

The only thing to watch out for here is that we need to coordinate the variables across the sub-queries. This is what the FROM CapitalOf AS c and later c.country syntax does. Let’s see if you can apply this:

Write SQL queries that correspond to to the following conjunctions:
- LocatedIn x Europe LanguageOf x Dutch
- LocatedIn Japan x CaptailOf x WashingtonDC

We can go on from here and cover disjunction, conditionals, and existentials, but I hope that the sub-pattern strategy pattern has become clear. This is one way to obtain SQL queries for ever FOL formula. There is much more to be said about this, but let’s leave it here.

As a final brain teaser:

Write SQL queries that corresponds to LocatedIn x Europe LanguageOf x English using only the patterns for and we’ve already discussed.

Solution

Here’s a list of queries that work:

LanguageOf UnitedStates x

1
2
3


SELECT language
FROM LanguageOf
WHERE country = 'United States';

LocatedIn Japan x

1
2
3


SELECT continent
FROM LocatedIn
WHERE country = 'Japan';

LocatedIn x x

1
2
3


SELECT country, continent
FROM LocatedIn
WHERE country = continent;

Here we go:

LanguageOf UnitedStates x

1
2
3
4
5
6
7
8


SELECT language
FROM Language
WHERE NOT EXISTS (
  SELECT *
  FROM Language
  WHERE country = 'United States'
    AND Language.language = language
);

LocatedIn Japan x

1
2
3
4
5
6
7
8


SELECT DISTINCT continent
FROM LocatedIn
WHERE NOT EXISTS (
  SELECT *
  FROM LocatedIn
  WHERE country = 'Japan'
    AND LocatedIn.continent = continent
);

LocatedIn x x

1
2
3
4
5
6
7
8


SELECT continent
FROM LocatedIn
WHERE NOT EXISTS (
  SELECT *
  FROM LocatedIn
  WHERE country = 'Japan'
    AND LocatedIn.continent = continent
);

And the last

LocatedIn x Europe LanguageOf x Dutch

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


SELECT country
FROM CapitalOf AS outer
WHERE
  -- LocatedIn(x, 'Europe')
  EXISTS (
    SELECT *
    FROM LocatedIn
    WHERE country = outer.country
      AND continent = 'Europe'
  )
  -- ¬Language(x, 'Dutch')
  AND NOT EXISTS (
    SELECT *
    FROM LanguageOf
    WHERE country = outer.country
      AND language = 'Dutch'
  );

LocatedIn Japan x CaptailOf x WashingtonDC

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


SELECT country
FROM CapitalOf AS outer
WHERE
  -- ¬ LocatedIn Japan x
  NOT EXISTS (
    SELECT *
    FROM LocatedIn
    WHERE country = 'Japan'
      AND continent = outer.country     
  )
  -- ¬CapitalOf x Washington D.C.
  AND NOT EXISTS (
    SELECT *
    FROM CapitalOf
    WHERE country = outer.country
      AND capital = 'Washington D.C.'
  );

Here we go:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


SELECT country
FROM CapitalOf AS outer
WHERE NOT (
    NOT EXISTS (
      SELECT *
      FROM LocatedIn
      WHERE country = outer.country
        AND continent = 'Europe'
    )
    AND
    NOT EXISTS (
      SELECT *
      FROM LanguageOf
      WHERE country = outer.country
        AND language = 'English'
    )
);

A much simpler code uses OR, but that wasn’t the question:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17



SELECT country
FROM CapitalOf AS outer
WHERE
  EXISTS (
    SELECT *
    FROM LocatedIn
    WHERE country = outer.country
      AND continent = 'Europe'
  )
  OR
  EXISTS (
    SELECT *
    FROM LanguageOf
    WHERE country = outer.country
      AND language = 'English'
  );