Tutorial 9. FOL inference
Exercise sheet
Unification
For each of the following pairs of terms determine whether they can be unified. If so, provide the unifier:
LiesBetween Munich y zandLiesBetween x Milan RomeSitsBeween Mary x xandSitsBetween x Jane yBetween x Rome Romeand Between Rome y x
Between Rome y x  BornIn fatherOf motherOf x London
BornIn fatherOf motherOf x London BornIn fatherOf y x
BornIn fatherOf y x Human x
Human x Human fatherOf x
Human fatherOf xHuman fatherOf y xandHuman x fatherOf y
Solution
- Unifiable with
[x / Munich, y / Milan, z / Rome]. - Not unifiable since
xwould need to be bothMaryandJane, which is impossible. - Not unifiable since one formula is a negation and the other isn’t.
- Unifiable with
[x / London, y / motherOf London] - Not unifiable since whatever
xwould be it can’t give youfatherOf x. - Unifiable by
[x / fatherOf y]
Robinson’s Algorithm
The first algorithms for unification is due to John Alan Robinson , the father of resolution.
To check whether two FOL literals can be unified, the algorithm proceeds as follows:
-
Check if either both formulas begin with a negation or neither does. If so, proceed. Otherwise, the formulas are not unifiable.
-
Check if the predicate in both formulas is the same. If it is, continue. If it is not, the formulas are not unifiable.
-
We can assume, at this point, that the form of the formulas is covered by one of the two cases:
-
Pⁿ s₁ … sₙandPⁿ t₁ … tₙ -
 Pⁿ s₁ … sₙ
Pⁿ s₁ … sₙ Pⁿ t₁ … tₙ
Pⁿ t₁ … tₙ
In both cases, to unify the formulas, we need to find a substitution σ, such that s₁σ = t₁σ, …, sₙσ = tₙσ, that is the result of substituting within these terms must make each pair identical.
To express this requirement, we make a list of these pairs:
Eq = [ [s₁, t₁], ..., [sₙ, tₙ] ]The algorithm aims to step-wise construct the desired substitution σ. We start with the empty substitution
σ = [ ], and go through each pair[sᵢ, tᵢ]of our list. We distinguish the following cases:-
Case 1:
sᵢ = tᵢ. The terms are already identical, we can remove them fromEq. -
Case 2.
sᵢ ≠ tᵢandsᵢis some variable, whiletᵢis not. First, check ifsᵢoccurs intᵢ. If so, like whensᵢ = xandtᵢ = fatherOf x, then we can stop the entire procedure since no unification is possible. Otherwise, we apply the substitution[sᵢ / tᵢ]to all other pairs, add it toσ, and remove the pair[sᵢ, tᵢ]from the set. -
Case 3.
sᵢ ≠ tᵢandtᵢis some variable, whilesᵢis not. Again, we first check iftᵢoccurs withinsᵢand terminate the entire algorithm if it does. Otherwise, we apply the substitution[tᵢ / sᵢ]to all other pairs, add it toσ, and remove the pair[sᵢ, tᵢ]from the set. -
Case 4.
sᵢ ≠ tᵢand neithersᵢnortᵢis a variable. Then we check the form ofsᵢandtᵢ. Only if they are of the following forms, we continue:
sᵢ = fᵐ s₁' … sₘ' and tᵢ = fᵐ t₁' … tₘ'That is, both terms are the result of applying the same function term to a sequence of terms. If they are not, unification is impossible and we can terminate the algorithm. If they are of this form, we add all the following corresponding pairs to
Eq:[ [s₁', s₂'], ..., [sₙ', tₙ'] ] -
-
By going through all the pairs, deleting pairs when substitutions are possible or trivial (Cases 1—3), and recursively adding new pairs (Case 4), one of two things will happen:
-
Either we hit a termination condition in one of the cases and conclude that unification isn’t possible.
-
Or we end up with an empty list and a full list of substitutions
σto apply. In that case,σis a unifier and the terms and thus literals are indeed unifiable.
-
Apply this algorithm to check your work in Exercise 1.
Solution
-
Steps 1. & 2. of the algorithm all succeed with no difficulty. So, we check the pairs:
E = {[Munich, y],[y, Milan], [z, Rome]Applying cases 2. and 3. gives us the substitution:
[x / Munich, y / Milan, z / Rome] -
Steps 1. & 2. of the algorithm all succeed with no difficulty. So, we check the pairs:
E = {[Mary, x], [x, Jane], [x, y]}Applying Case 3. with
[Mary, x]gives us:{[Mary, Jane], [Mary, y]}Case 4. tells us to stop when we reach
[Mary, Jane]. There is no substitution possible. -
Check 1. already fails, the two aren’t unifiable.
-
Steps 1. & 2. of the algorithm all succeed with no difficulty. So, we check the pairs:
E = {[fatherOf motherOf x, fatherOf y], [London, x]}Step 4 gives us for
[fatherOf motherOf x, fatherOf y]:E = {[motherOf x, y], [London, x]}Applying rule 3. and 4. gives us the substitution:
[x / London, y / motherOf x]which unifies the two formulas.
-
Steps 1. & 2. of the algorithm all succeed with no difficulty. So, we check the pairs:
E = { [fatherOf y, x], [x, fatherOf y]}which gives us by rule 3 the set
E = { [fatherOf y, fatherOf y] }with substitution
[x / fatherOf y], which terminates the algorithm.
Skolemization
Skolemize the following formulas:
-
(
 y₁ Human y₁
y₁ Human y₁

 x₁ Mortal x₁)
x₁ Mortal x₁) -
 x₁(
x₁(
 x₂
x₂
 y₁(IsFriendOf x₁ y₁
y₁(IsFriendOf x₁ y₁
 IsFriendOf x₂ y₁)
IsFriendOf x₂ y₁)

 y₂
y₂
 IsFriendOf x₁ y₂)
IsFriendOf x₁ y₂) -
 y₁
y₁
 y₂ IsFriendOf y₁ y₂
y₂ IsFriendOf y₁ y₂
Solution
-
(Human
skolem₁
 x₁ Mortal x₁)
x₁ Mortal x₁) -
 x₁(
x₁(
 x₂(IsFriendOf x₁
x₂(IsFriendOf x₁ skolem₁x₁ x₂ IsFriendOf x₂
IsFriendOf x₂ skolem₁x₁ x₂)
 IsFriendOf x₁
IsFriendOf x₁ skolem₂x₁) -
IsFriendOf
skolem₁skolem₂
Drinker Paradox
Consider the following inference:
 x InPub x
x InPub x

 x (InPub x
x (InPub x
 (IsDrinking x
(IsDrinking x

 x(InPub x
x(InPub x
 IsDrinking x)))
IsDrinking x)))In natural language: There’s somebody in the pub, so there’s somebody in the pub, such that if they are drinking, then everybody in the pub is drinking. This is known as the drinker paradox .
Use the method of resolution to show that this inference is deductively valid in FOL. That is:
-
Form the set of the premise and negation of conclusion.
-
Transform all formulas into equisatisfiable CNF. Note that the Skolemization of an existential that doesn’t depend on any universals is just a constant
skolem. It’s important to document your work, which transformations you’re applying, but you can apply several steps simultaneously. -
Apply resolution with unification to derive the empty sequent { }. And conclude that the initial set is unsatisfiable and the inference thus valid.
Solution
-
The set is:
{ x InPub x,
x InPub x,

 x (InPub x
x (InPub x
 (IsDrinking x
(IsDrinking x

 x(InPub x
x(InPub x
 IsDrinking x)))}
IsDrinking x)))} -
Here are the results of the procedure:
-
The transformation of
 x InPub x just involves one step (Skolemization), which immediately gives us:InPub
x InPub x just involves one step (Skolemization), which immediately gives us:InPubskolem₁ -
The other formula requires some more steps:
-

 x (InPub x
x (InPub x
 (IsDrinking x
(IsDrinking x

 x(InPub x
x(InPub x
 IsDrinking x)))}
IsDrinking x)))} -
Two applications of r₀ give:

 x (InPub x
x (InPub x
 (
(
 IsDrinking x
IsDrinking x

 x(
x(
 InPub x
InPub x
 IsDrinking x)))
IsDrinking x))) -
Then we push negations inwards with r₁-r₃ and r₆:
 x (
x (
 InPub x
InPub x
 (IsDrinking x
(IsDrinking x

 x (InPub x
x (InPub x

 IsDrinking x)))
IsDrinking x))) -
Next we make the variables unique:
 x₁ (
x₁ (
 InPub x₁
InPub x₁
 (IsDrinking x₁
(IsDrinking x₁

 y₁ (InPub y₁
y₁ (InPub y₁

 IsDrinking y₁)))
IsDrinking y₁))) -
Then we Skolemize:
 x₁ (
x₁ (
 InPub x₁
InPub x₁
 (IsDrinking x₁
(IsDrinking x₁
 (InPub
(InPub skolem₂x₁
 IsDrinking
IsDrinking skolem₂x₁))) -
And drop the universal:
( InPub x₁
InPub x₁
 (IsDrinking x₁
(IsDrinking x₁
 (InPub
(InPub skolem₂x₁
 IsDrinking
IsDrinking skolem₂x₁))) -
Finally, repeated distribution gives us:
( InPub x₁
InPub x₁
 IsDrinking x)
IsDrinking x)
 (
(
 InPub x
InPub x
 InPub
InPub skolem₂ x) (
(
 InPub x
InPub x

 IsDrinking
IsDrinking skolem₂ x))
-
-
For the resolution, we therefore work with the sets:
{InPubskolem₁} { InPub x₁ , IsDrinking x₁}{
InPub x₁ , IsDrinking x₁}{ InPub x₁, InPub
InPub x₁, InPub skolem₂ x} { InPub x₁,
InPub x₁,
 IsDrinking
IsDrinking skolem₂ x₁}Here’s a derivation of { } from this using resolution:

-
Natural deduction
Find logical proofs in FOL natural deduction for the following logical
laws. Note that some of these require open Classical.
Duality Laws
-

 xA(x)
xA(x)

 x
x
 A(x)
A(x) -
 x
x
 A(x)
A(x)


 xA(x)
xA(x) -

 xA(x)
xA(x)

 x
x
 A(x)
A(x) -
 x
x
 A(x)
A(x)


 xA(x)
xA(x)
Distribution Laws
-
 x(A(x)
x(A(x)
 B(x))
B(x))

 xA(x)
xA(x)

 xB(x)
xB(x) -
 xA(x)
xA(x)

 xB(x)
xB(x)

 x (A(x)
x (A(x)
 B(x))
B(x)) -
 x(A(x)
x(A(x)
 B(x))
B(x))

 xA(x)
xA(x)

 xB(x)
xB(x) -
 x A(x)
x A(x)

 x B(x)
x B(x)

 x(A(x)
x(A(x)
 B(x))
B(x))
Interaction Laws
-
 xA(x)
xA(x)

 xA(x)
xA(x) -
 x
x
 yR(x,y)
yR(x,y)

 y
y
 xR(x,y)
xR(x,y) -
 xA(x)
xA(x)
 C
C

 x(A(x)
x(A(x)
 C), assuming that x is not free in C
C), assuming that x is not free in C -
 xA(x)
xA(x)
 C
C

 x(A(x)
x(A(x)
 C), assuming that x is not free in C.
C), assuming that x is not free in C.
Solution
Duality Laws
-

 xA(x)
xA(x)

 x
x
 A(x) (This one’s a bit more difficult)
A(x) (This one’s a bit more difficult)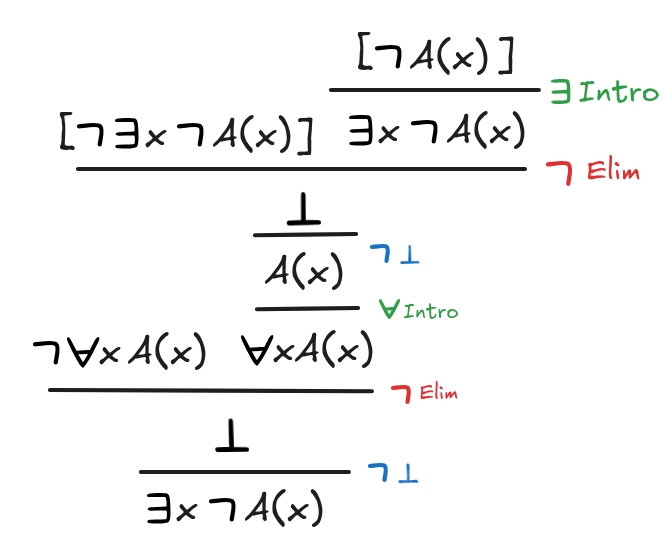
-
 x
x
 A(x)
A(x)


 xA(x)
xA(x)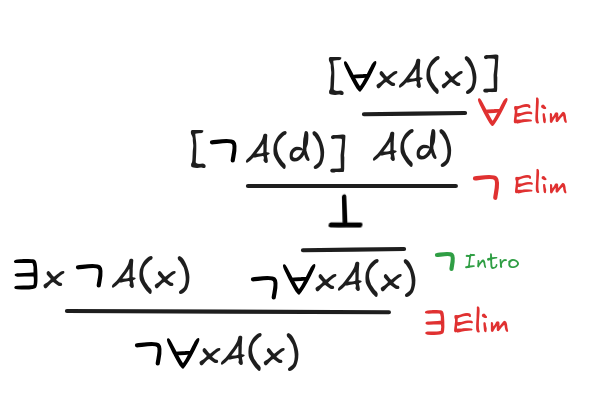
-

 xA(x)
xA(x)

 x
x
 A(x)
A(x)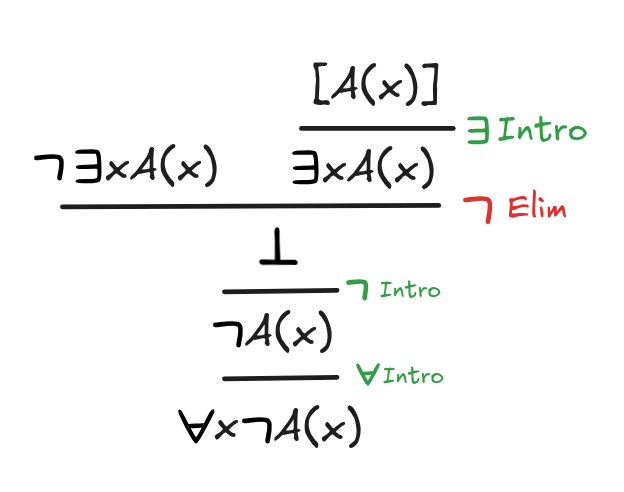
-
 x
x
 A(x)
A(x)


 xA(x)
xA(x)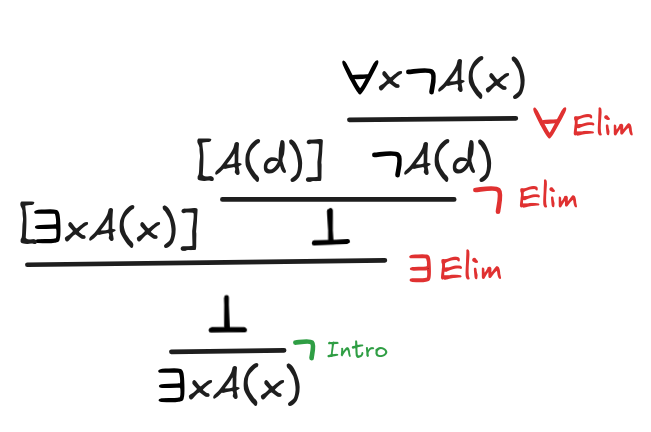
Distribution Laws
-
 x(A(x)
x(A(x)
 B(x))
B(x))

 xA(x)
xA(x)

 xB(x)
xB(x)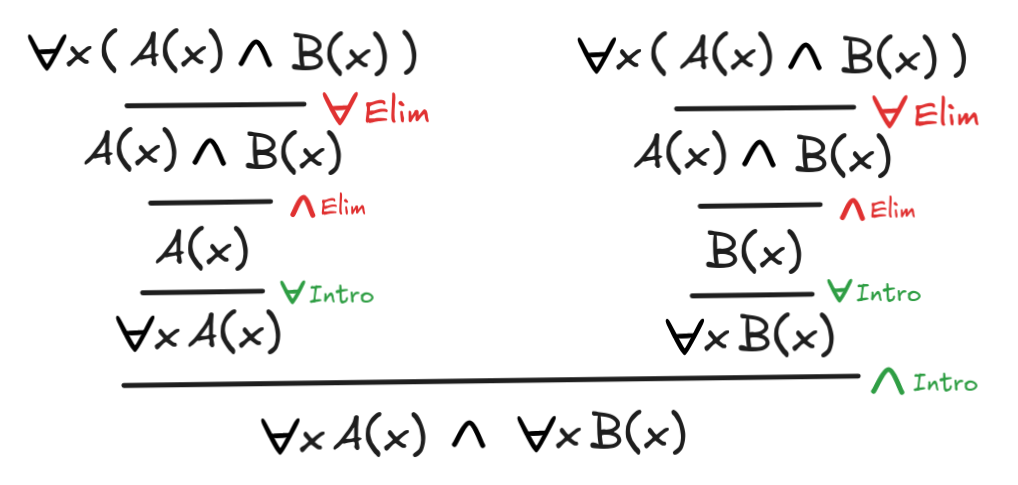
-
 xA(x)
xA(x)

 xB(x)
xB(x)

 x (A(x)
x (A(x)
 B(x))
B(x))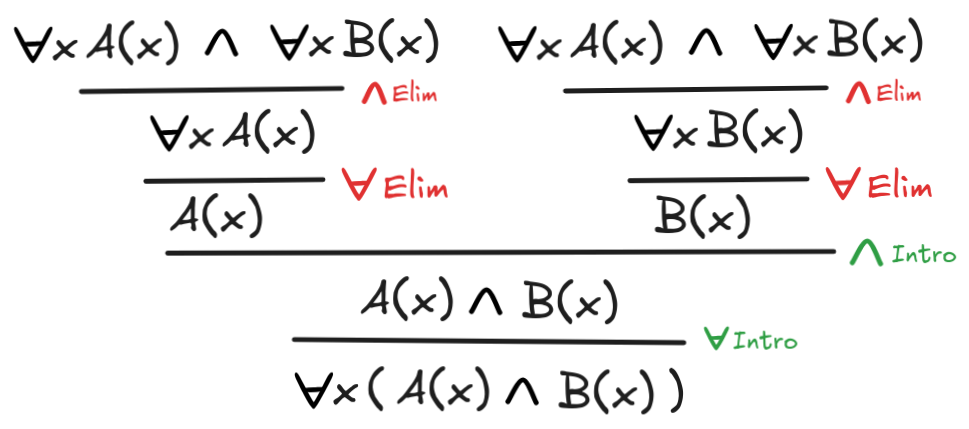
-
 x(A(x)
x(A(x)
 B(x))
B(x))

 xA(x)
xA(x)

 xB(x)
xB(x)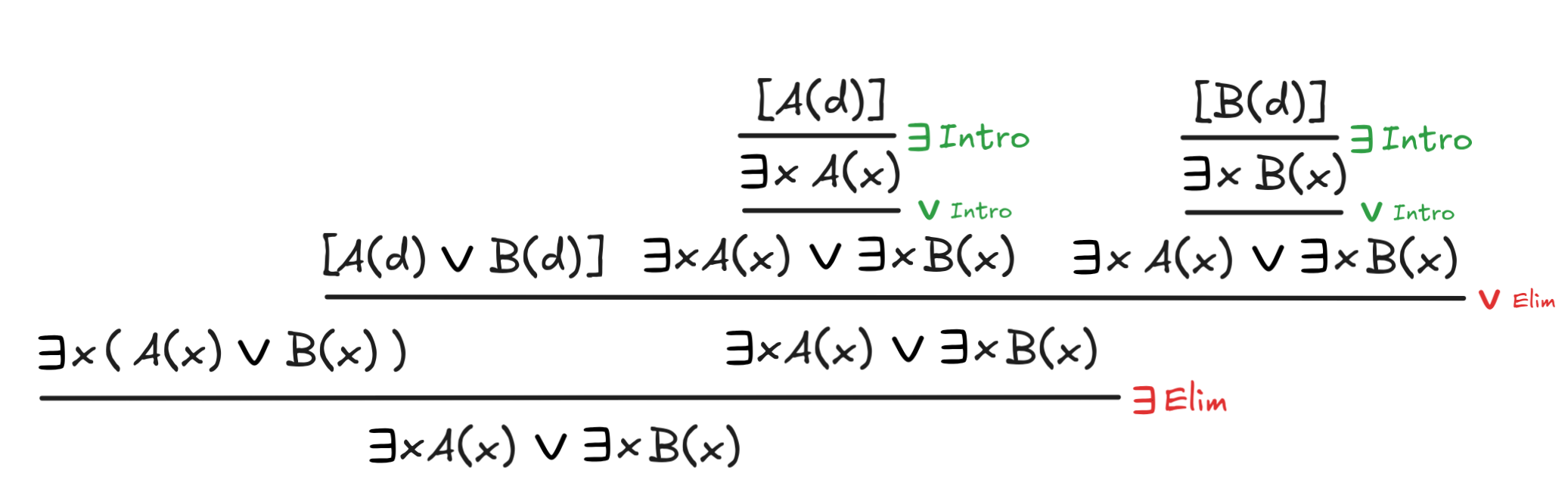
-
 x A(x)
x A(x)

 x B(x)
x B(x)

 x(A(x)
x(A(x)
 B(x))
B(x))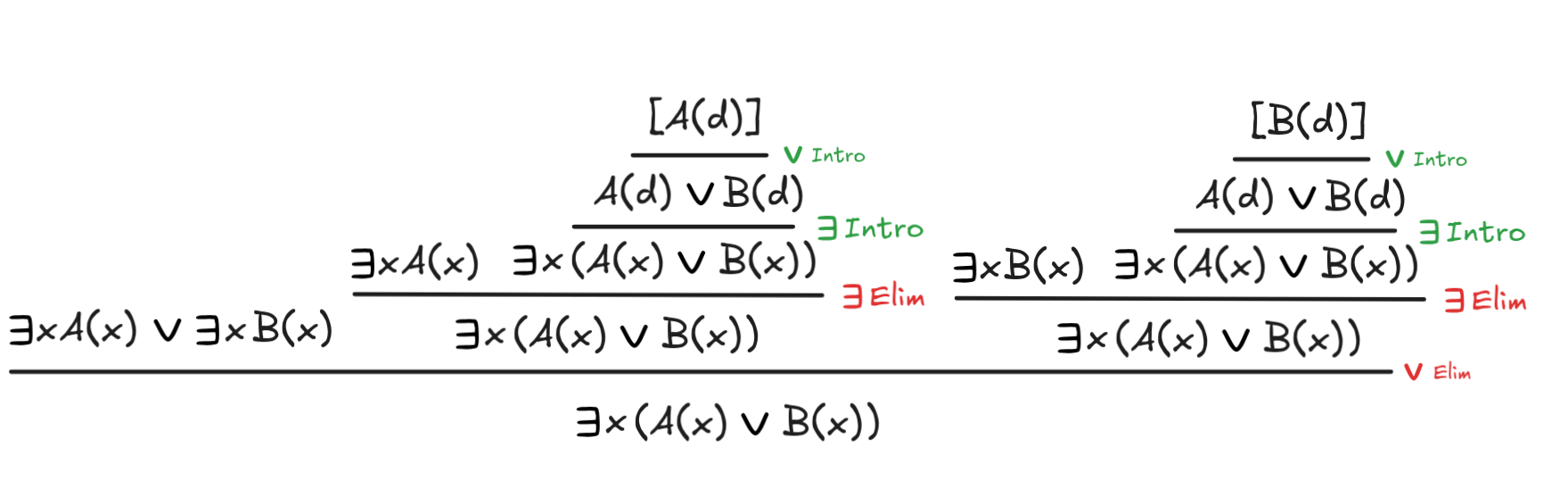
Interaction Laws
-
 xA(x)
xA(x)

 xA(x)
xA(x)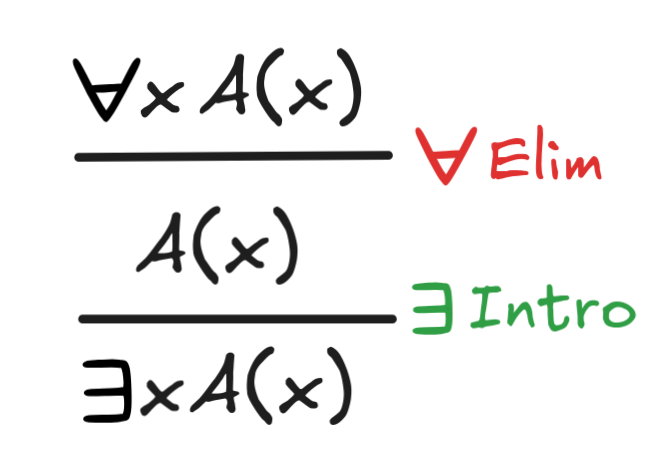
-
 x
x
 yR(x,y)
yR(x,y)

 y
y
 xR(x,y)
xR(x,y)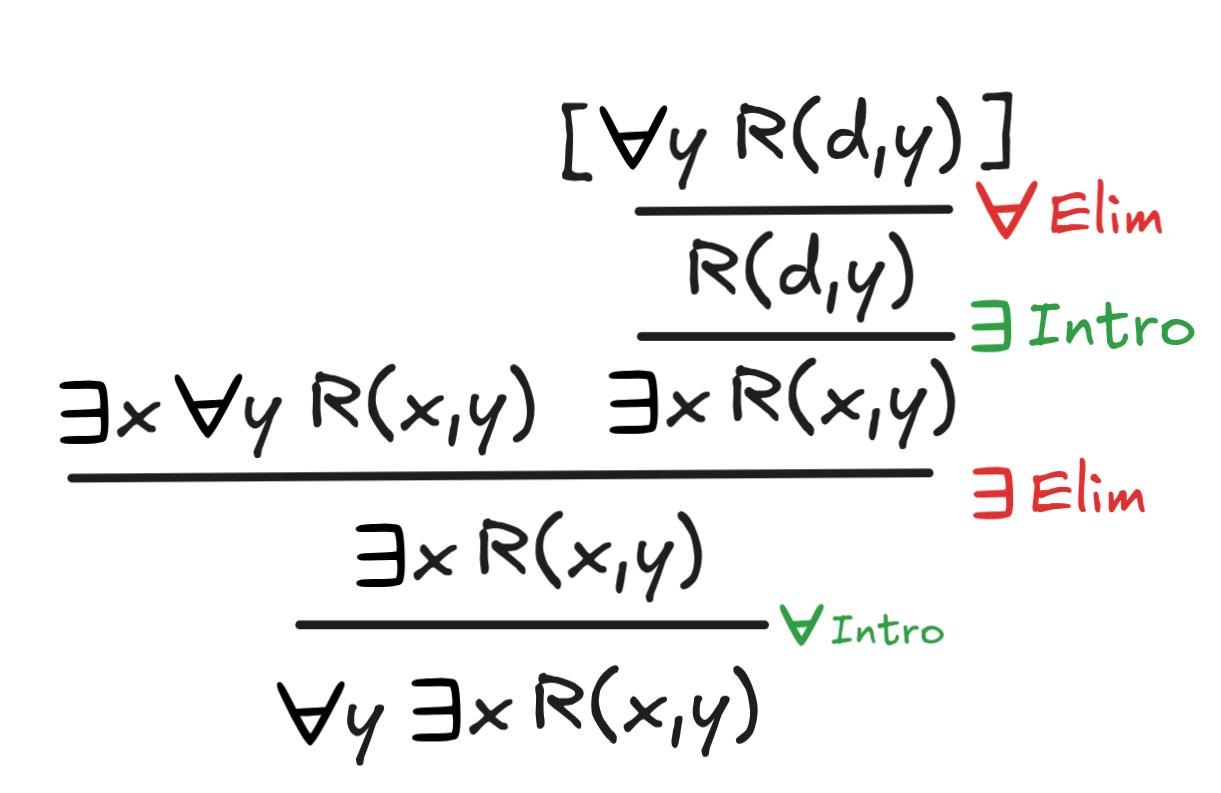
-
 xA(x)
xA(x)
 C
C

 x(A(x)
x(A(x)
 C), assuming that x is not free in C
C), assuming that x is not free in C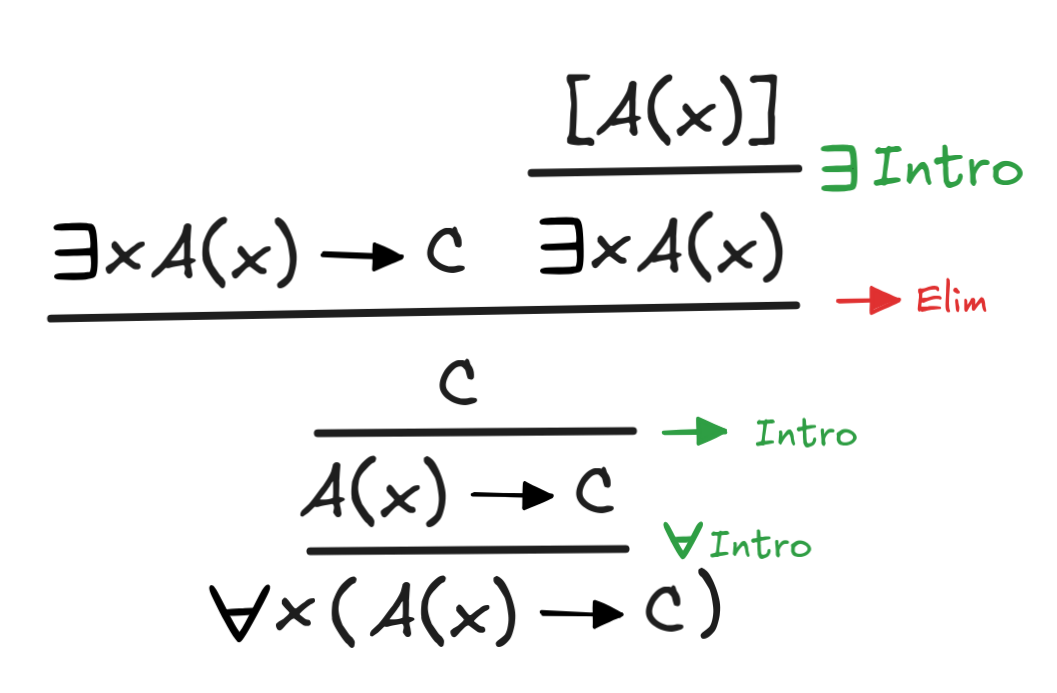
-
 xA(x)
xA(x)
 C
C

 x(A(x)
x(A(x)
 C), assuming that x is not free in C.
C), assuming that x is not free in C.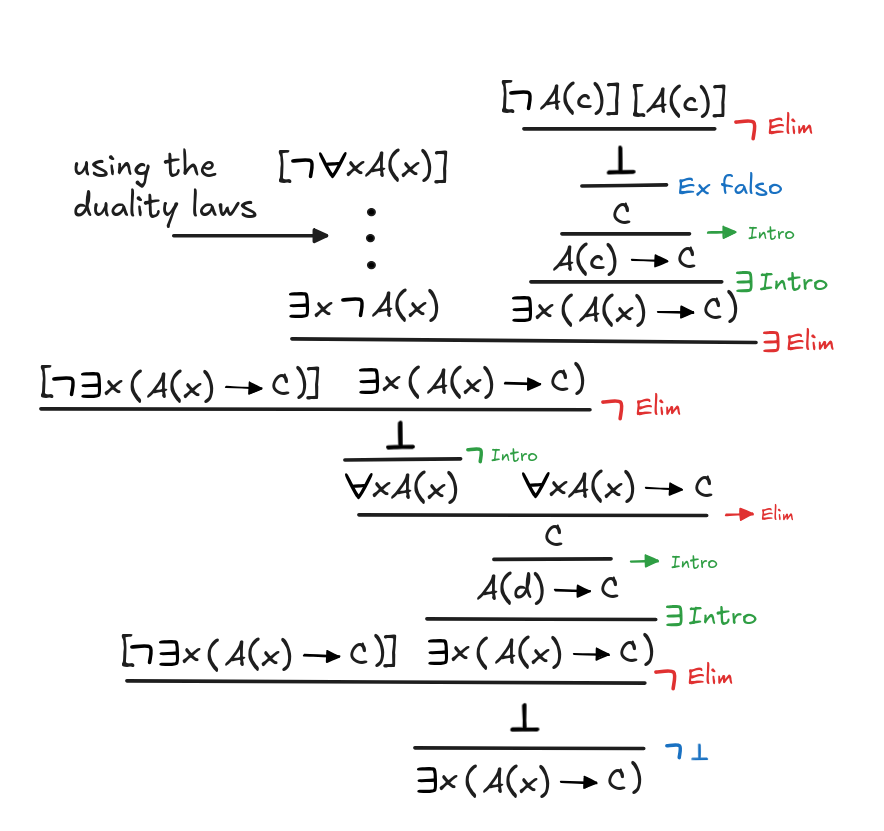
Lean
Verify your work from the previous exercise in Lean. Here’s a template for the work. You can follow the link below to work in the interactive environment.

|
|
Follow this link to work in the digital playground.
Solution
Credit: Alexander Apers

|
|
You can review the code in the lean plaground by following this link .