Browse course

Tutorial 10. Many-valued logics

Exercise sheet
K3-Sat Solving  

In class, we’ve implemented a counter-model searcher for K3 inferences using SQL in db-fiddle . Use the machinery to check whether the following inferences are K3 valid or not:

  1. (RAIN Disjunction (RAIN Conjunction SUN)) Therefore SUN
  2. SUN Therefore RAIN Conjunction Negation RAIN
  3. SUN, Negation SUN Therefore RAIN
  4. RAIN Conjunction Negation SUN Therefore Negation ( Negation RAIN Disjunction SUN)
  5. WIND Therefore Negation (RAIN Conjunction Negation RAIN)
  6. RAIN Therefore RAIN Disjunction Negation RAIN
Solution

The following db-fiddle contains queries for each of the above inferences. The ones that return non-empty tables have countermodels, which are given by the return values. The annotations explain how to interpret the tables.

K3-Laws  

In fact, you can use a similar method to verify the laws of Kleene algebra using SQL.

Here are, for example, the queries to verify the commutativity of OR and AND:

SQL_Logo 
1
2
3
4
5
6

 SELECT * 
 FROM ValuePairs
 WHERE
	(X OR Y) != (Y OR X)
  OR
	(X AND Y) != (Y AND X);

Verify the remaining Kleene laws like this.

Note that for the laws with 3 variables, you need to create a table ValueTriples for the method to work.

Solution

The following db-fiddle contains code that verifies all laws. There are three queries, one for the laws with one variables, one for laws with two variables, and one for laws with three variables. The queries are structured such that it would return a valuation iff at least one of the laws fails. They don’t return anything so the laws hold.

Łukasiewicz conditionals  

In K3, we’ve defined a semantics for conditionals by saying that

v(A Implication B) = (NOT A) OR B

This gives rise to the Kleene logic K3. But interestingly, in this logic, it’s not a logical law that RAIN Implication RAIN—there are countermodels, where this statement isn’t true.

But there’s an alternative system of 3-valued logic, which is defined just like Kleene logic, except that it uses the following truth-table to interpret the conditional:

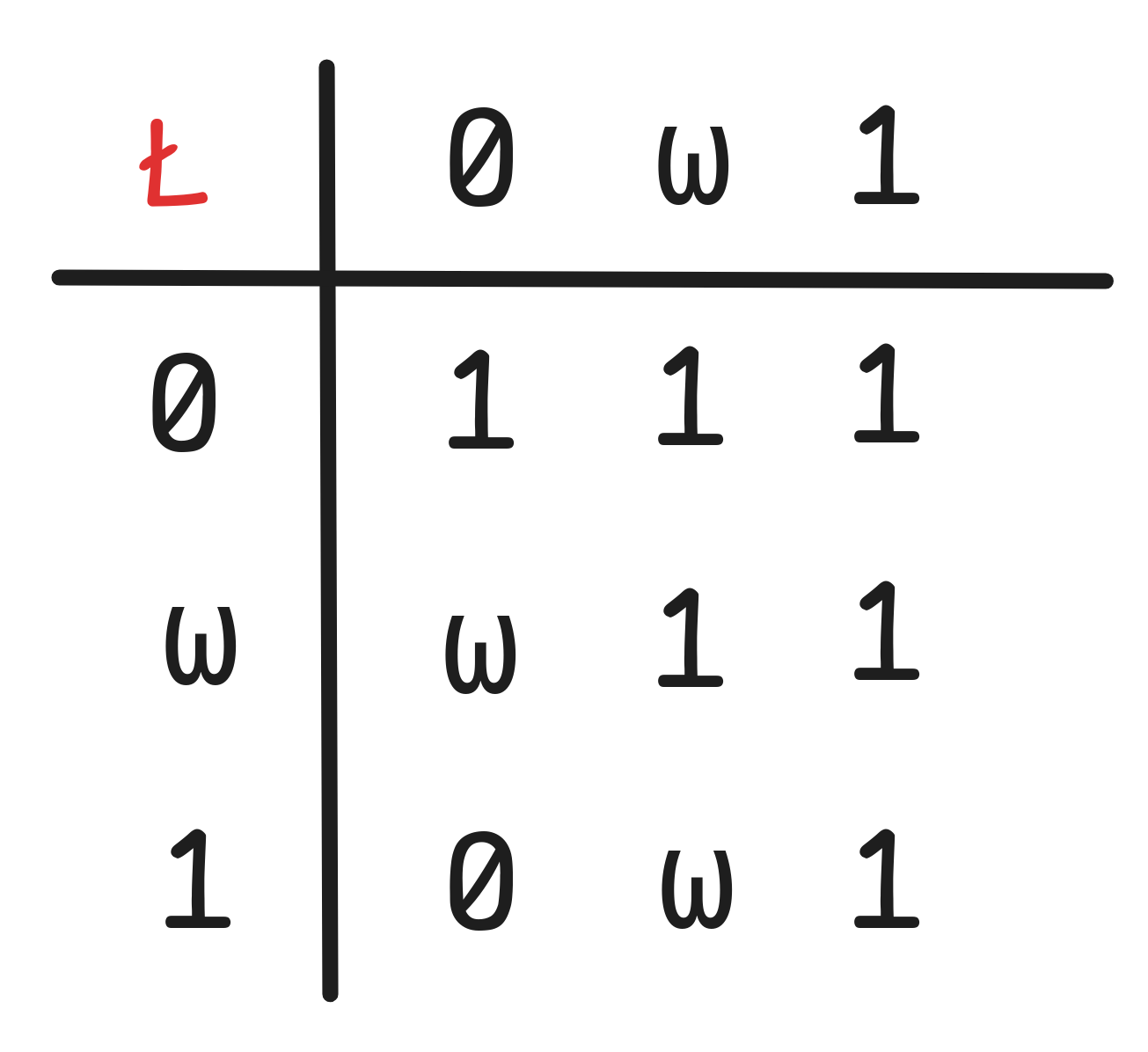
That is, in this system,

v(A Implication B) = A Ł B

This logic is called Łukasiewicz logic, Ł.

  1. Verify that there exists a K3 model, where RAIN Implication RAIN is not true.

  2. Verify that there RAIN Implication RAIN is true in all Ł models.

  3. Is MP valid in Ł-logic?

Solution

  1. Consider the K3-model where v(RAIN) = ω. In this model, we have

    v(RAIN Implication RAIN) = (NOT v(RAIN)) OR v(RAIN) = (NOT ω) OR ω = ω

    And since ω ≠ 1, this is a model where the formula isn’t true.

  2. we have that v(RAIN Implication RAIN) = v(RAIN) Ł v(RAIN). That is, we’re dealing with an expression of the form X Ł X. If we go to the table for Ł, we note that for identical inputs, the values (on the diagonal) are always 1. In other words, the formula is true in all models.

  3. Suppose that v(A) = 1 and v(A Implication B) = 1. Inspecting the table for Ł, we can see that there is one and only one configuration of values that makes this possible, namely the one where v(B) = 1.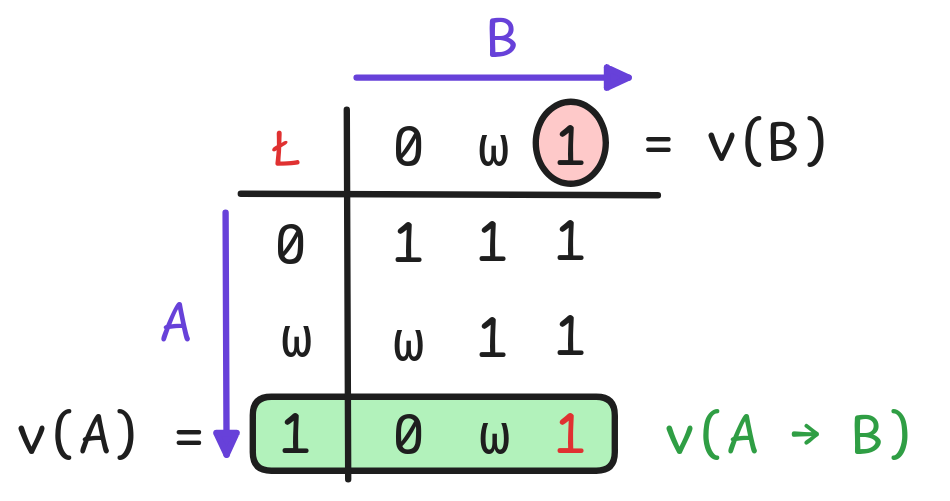

Fuzzy Predicates  

Suppose we’ve got a language with predicates Fast¹ and Slow¹, which describe the speed of a car and apply to terms for speed (like 10 km/h).

  1. Describe a model for these predicates by means of a diagram, in which there is a “gray area” between fast and slow.

  2. Add to the language two fuzzy constants break and accelerate. Formulate a system of fuzzy rules that keep the car in the gray area between fast and slow, while avoiding breaking and accelerating simultaneously.

Solution

  1. There are different ways of interpreting “gray area”.

    • Here’s an interpretation, according to which “gray area” means that there’s an area where the car is both fully not slow and fully not fast:

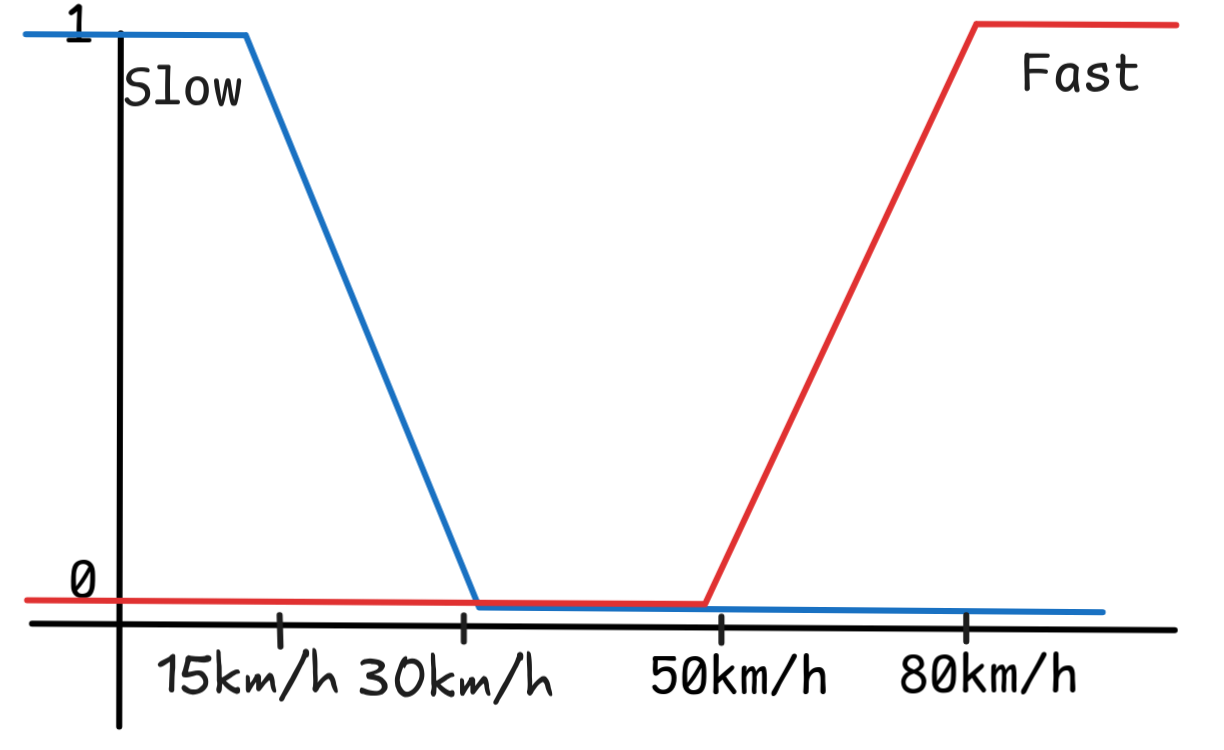
    • Here’s an interpretation, where “gray area” means that there’s an area where the car is both half-way fast and half-way slow:

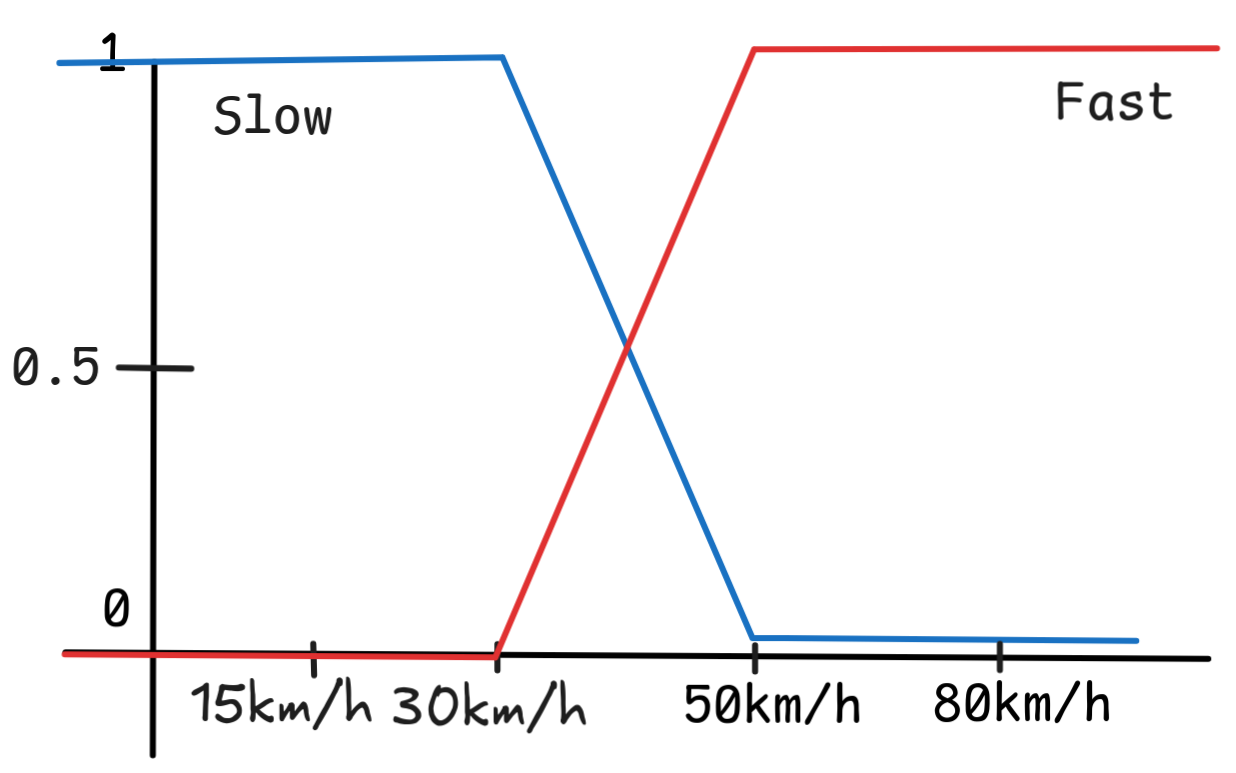
    These are, of course, other models, but these two will do.

  2. How such rules could look like highly depends on the model we chose to interpret Fast and Slow:

    • In our first model, the following rules will do:

      Fast x Long Rightarrow break
      Slow x Long Rightarrow accelerate

      In this model, our car will never break and accelerate at the same time.

    • In our second model, the same rules will lead to situations where we’re breaking and accelerating at the same time: if we pick an x where Left semantic bracket Slow x Right semantic bracket = Left semantic bracket Fast x Right semantic bracket = 0.5, we’ll have Left semantic bracket break Right semantic bracket = Left semantic bracket accelerate Right semantic bracket = 0.5. But they will keep the car in the “gray area”.

Fuzzy Logic  

In class, we’ve seen that in fuzzy logic, disjunctive syllogism fails: there are formulas A,B, such that

Negation A, A Disjunction B nvDash B

Modify the example to show that in fuzzy logic, also the principle of explosion fails, that is there are formulas A,B, such that

A, Negation A nvDash B

Solution

Let’s take for A a statement which, in a suitable model, is both “half-true”, that is, has value 0.5. For example, Fast 45km/h could be such that Left semantic bracket Fast 45km/h Right semantic bracket = 0.5. It follows by the semantics for Negation that also Left semantic bracket Negation Fast 45km/h Right semantic bracket = 0.5. That means that

min( Left semantic bracket Fast 45km/h Right semantic bracket , Left semantic bracket Negation Fast 45km/h Right semantic bracket ) = 0.5

If we then take a statement for B, which is certainly false, such as Fast 0kmh, meaning Left semantic bracket Fast 0km/h Right semantic bracket = 0, we have a clear countermodel:

min( Left semantic bracket Fast 45km/h Right semantic bracket , Left semantic bracket Negation Fast 45km/h Right semantic bracket ) = 0.5 ≥ 0 = Left semantic bracket Fast 0km/h Right semantic bracket

So the inference

A, Negation A nvDash B
is invalid.