Tutorial 7. Logical proofs
Exercise sheet
Proof systems
Let’s trial run the different proof systems. For each of the following, provide a logical proof in our Hilbert calculus, sequent calculus, and tableaux.
-
A
 A
A
 (A
(A
 B)
B) -
A
 (A
(A
 B)
B)
 A
A
Solution
-
Here we go:
-
Hilbert:
- A (Premise)
- A
 (A
(A
 (A
(A
 B)) (Axiom 6 with B = A
B)) (Axiom 6 with B = A
 B)
B) - (A
 (A
(A
 B)) (1., 2., MP)
B)) (1., 2., MP)
-
Sequent:
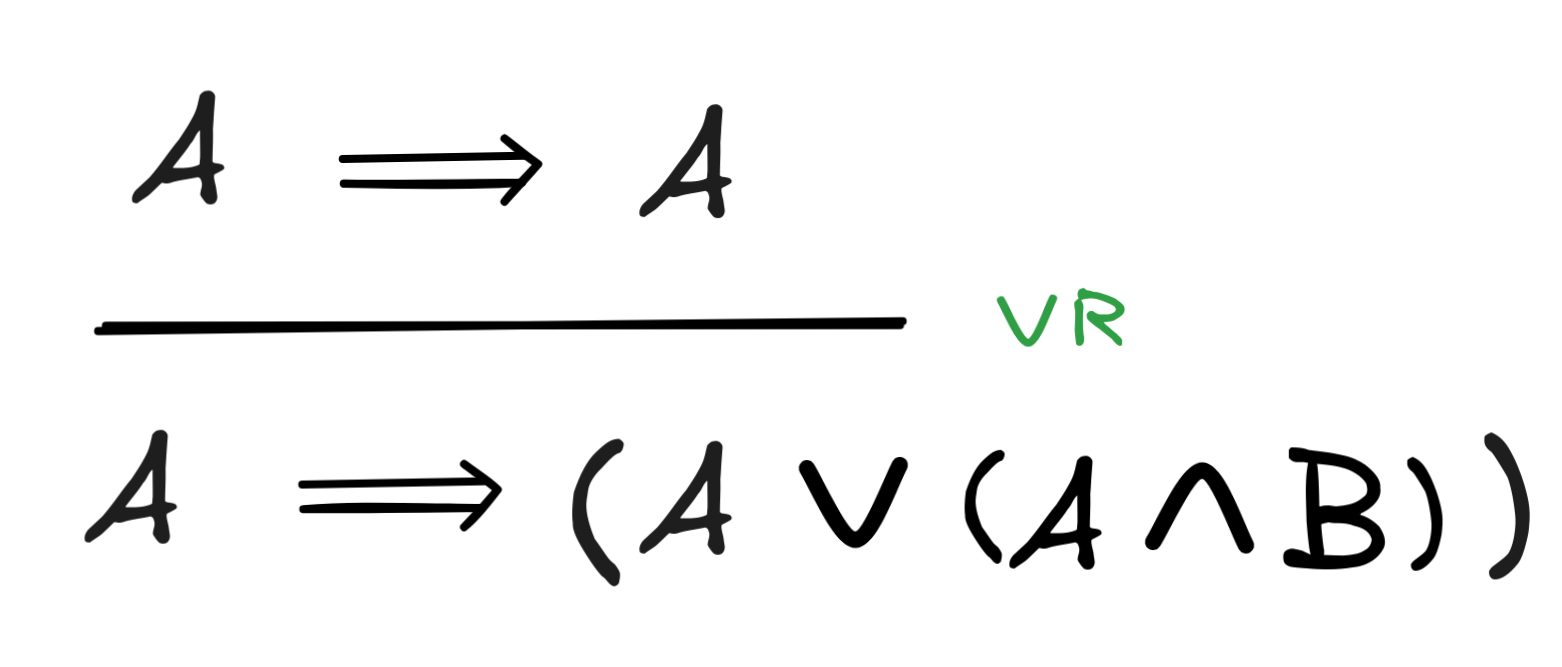
-
Tableaux:
-
-
Here we go:
-
Hilbert:
-
A
 (A
(A
 B) (Premise)
B) (Premise) -
(A
 A)
A)
 (((A
(((A
 B)
B)
 A)
A)
 ((A
((A
 (A
(A
 B))
B))
 A)) (Axiom 7.)
A)) (Axiom 7.) -
(A
 A) (Theorem from textbook)
A) (Theorem from textbook) -
((A
 B)
B)
 A)
A)
 ((A
((A
 (A
(A
 B))
B))
 A)(2., 3., MP)
A)(2., 3., MP) -
(A
 B)
B)
 A) (Axiom 5.)
A) (Axiom 5.) -
((A
 (A
(A
 B))
B))
 A)(4., 5., MP)
A)(4., 5., MP) -
A (1., 6., MP)
-
-
Sequent:
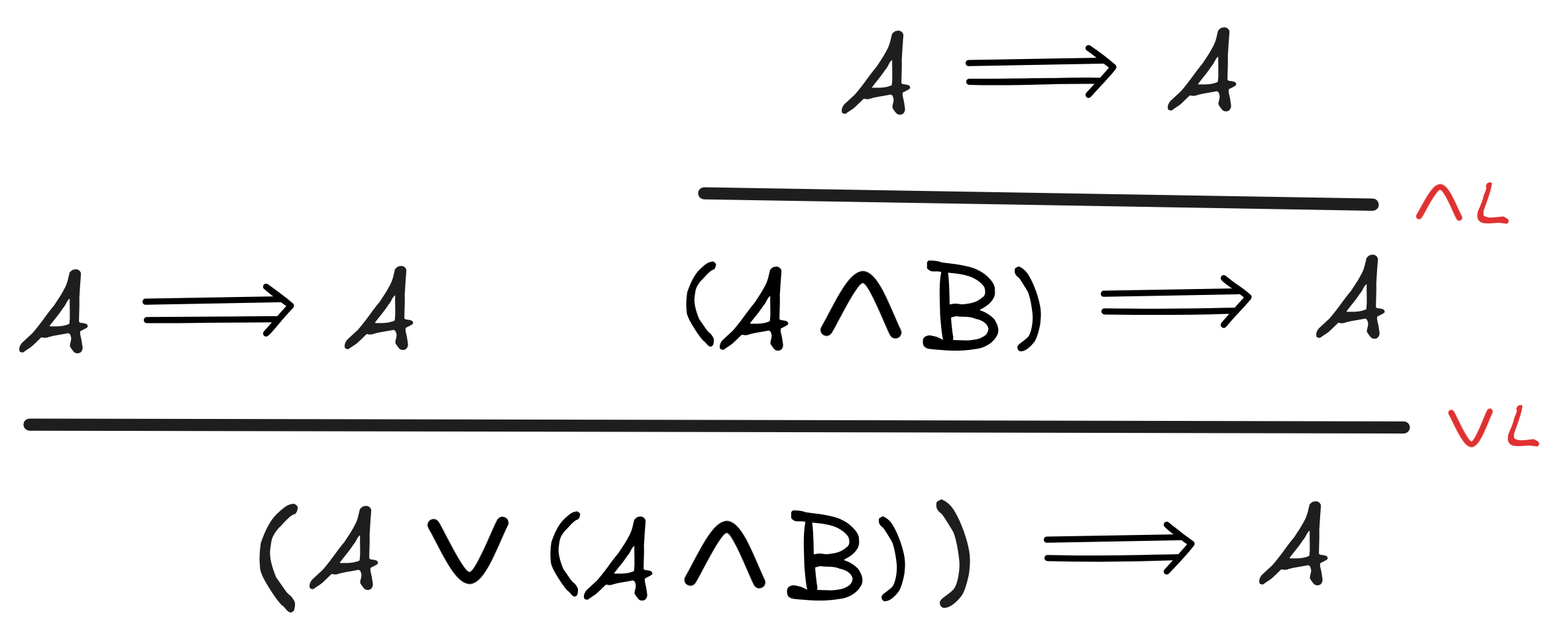
-
Tableaux:
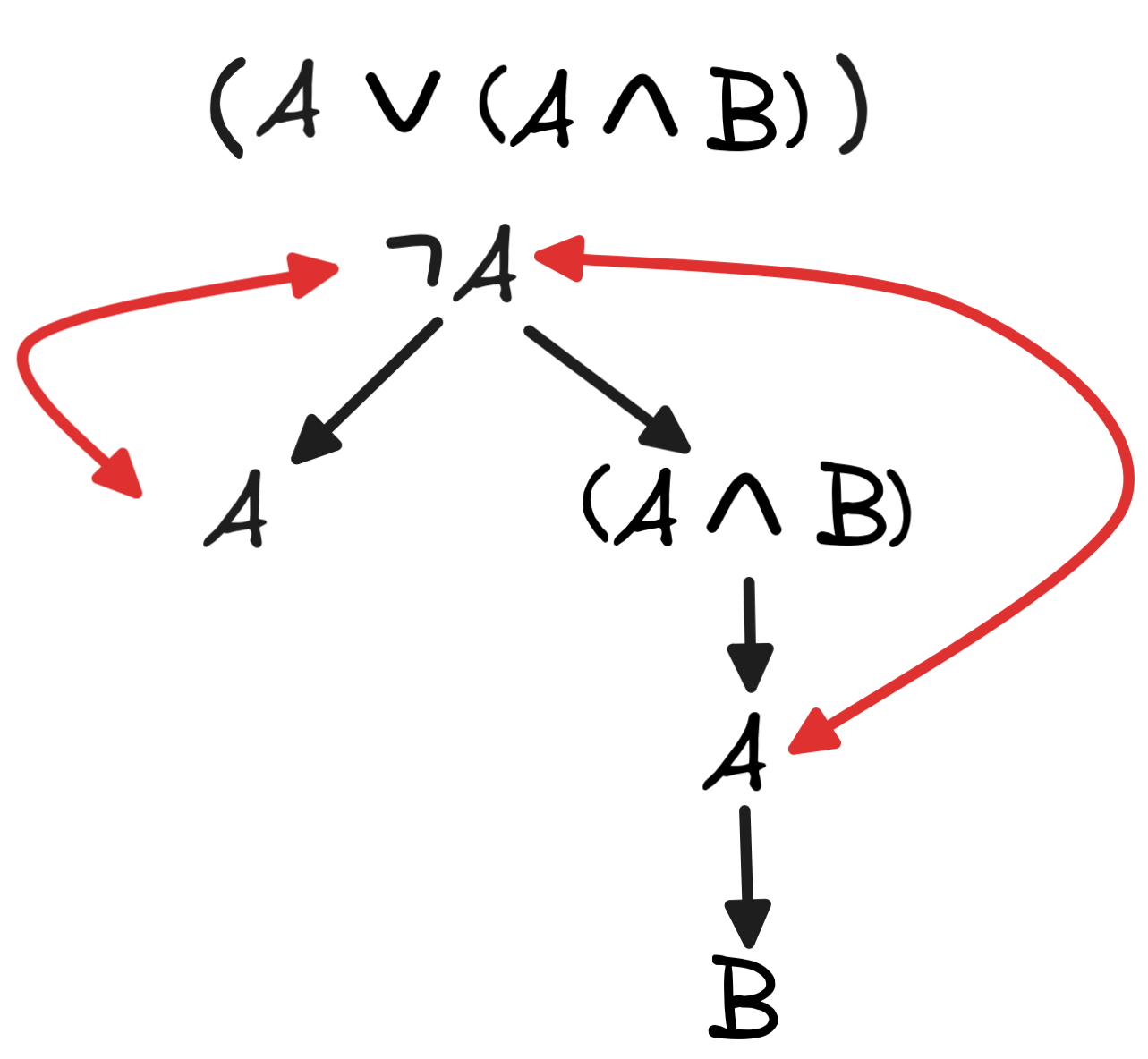
-
Natural deduction
For this exercise, you do a deep dive into natural deduction: below are a series
of laws to prove for arbitrary formulas A,B,C. Some require the rule

 , take note of which ones.
, take note of which ones.
Conjunction and Disjunction
-
A
 (B
(B
 C)
C)
 (A
(A
 B)
B)
 (A
(A
 C)
C) -
(A
 B)
B)
 (A
(A
 C)
C)
 A
A
 (B
(B
 C)
C) -
A
 (B
(B
 C)
C)
 (A
(A
 B)
B)
 (A
(A
 C)
C) -
(A
 B)
B)
 (A
(A
 C)
C)
 A
A
 (B
(B
 C)
C)
Negation
-
A


 A
A -

 A
A
 A
A -
 (A
(A
 B)
B)

 A
A

 B
B -
 A
A

 B
B

 (A
(A
 B)
B) -
 (A
(A
 B)
B)

 A
A

 B
B -
 A
A

 B
B

 (A
(A
 B)
B)
Conditionals
-
 A
A
 B
B
 A
A
 B
B -
A
 B
B

 A
A
 B
B -
(
 A
A
 A)
A)
 A
A -
(A
 B)
B)
 (
(
 B
B

 A)
A) -
(
 B
B

 A)
A)
 (A
(A
 B)
B)
Solution
Conjunction and Disjunction
-
A
 (B
(B
 C)
C)
 (A
(A
 B)
B)
 (A
(A
 C)
C)This solution is interactive! Click through the slides to get an explanation of how to find the derivation:
-
(A
 B)
B)
 (A
(A
 C)
C)
 A
A
 (B
(B
 C)
C) 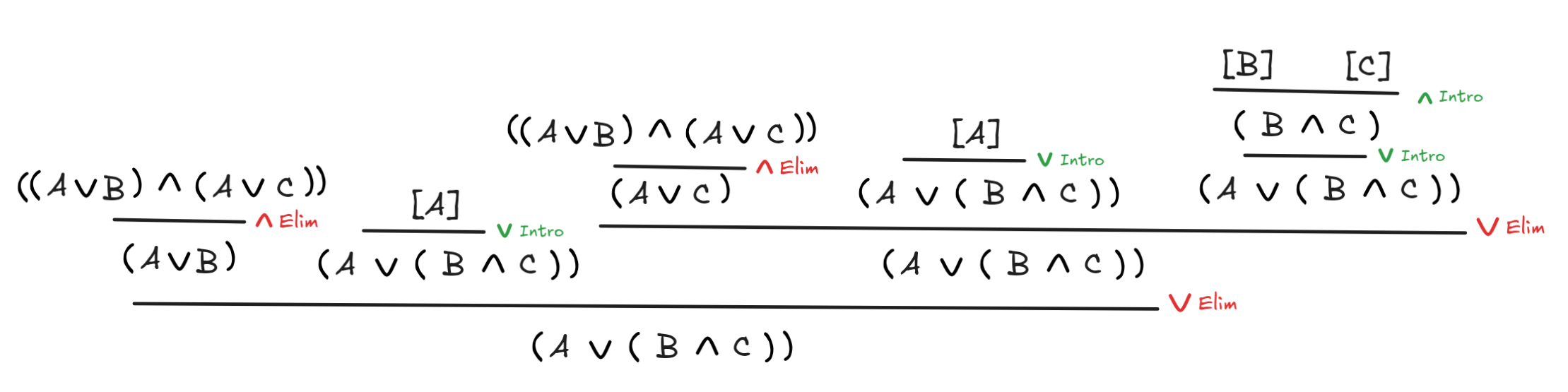
-
A
 (B
(B
 C)
C)
 (A
(A
 B)
B)
 (A
(A
 C)
C)This solution is interactive! Click through the slides to get an explanation of how to find the derivation:
-
(A
 B)
B)
 (A
(A
 C)
C)
 A
A
 (B
(B
 C)
C) 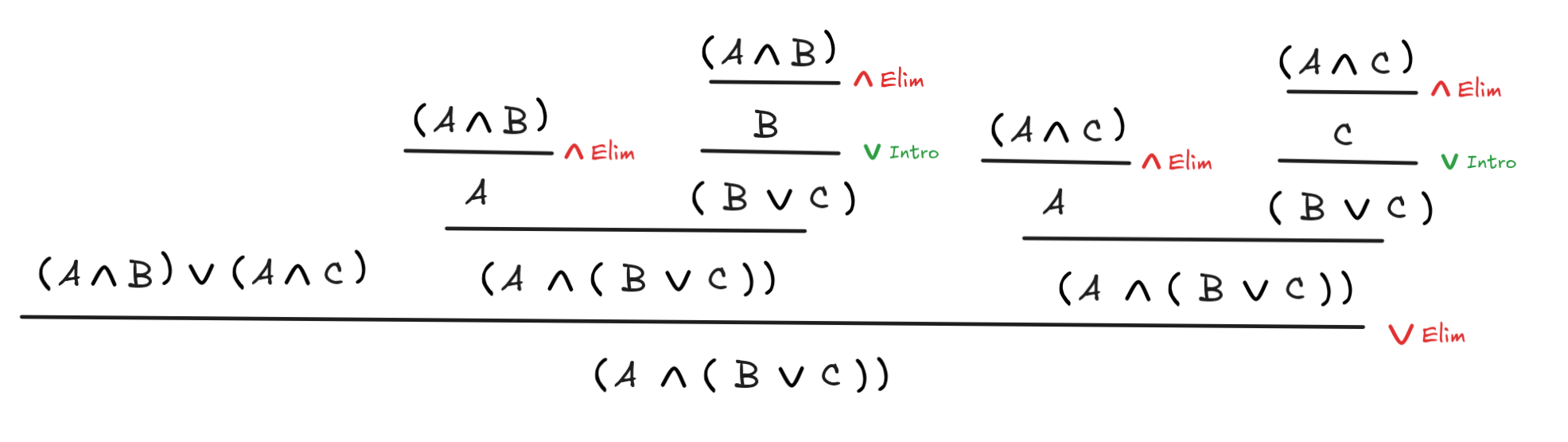
Negation
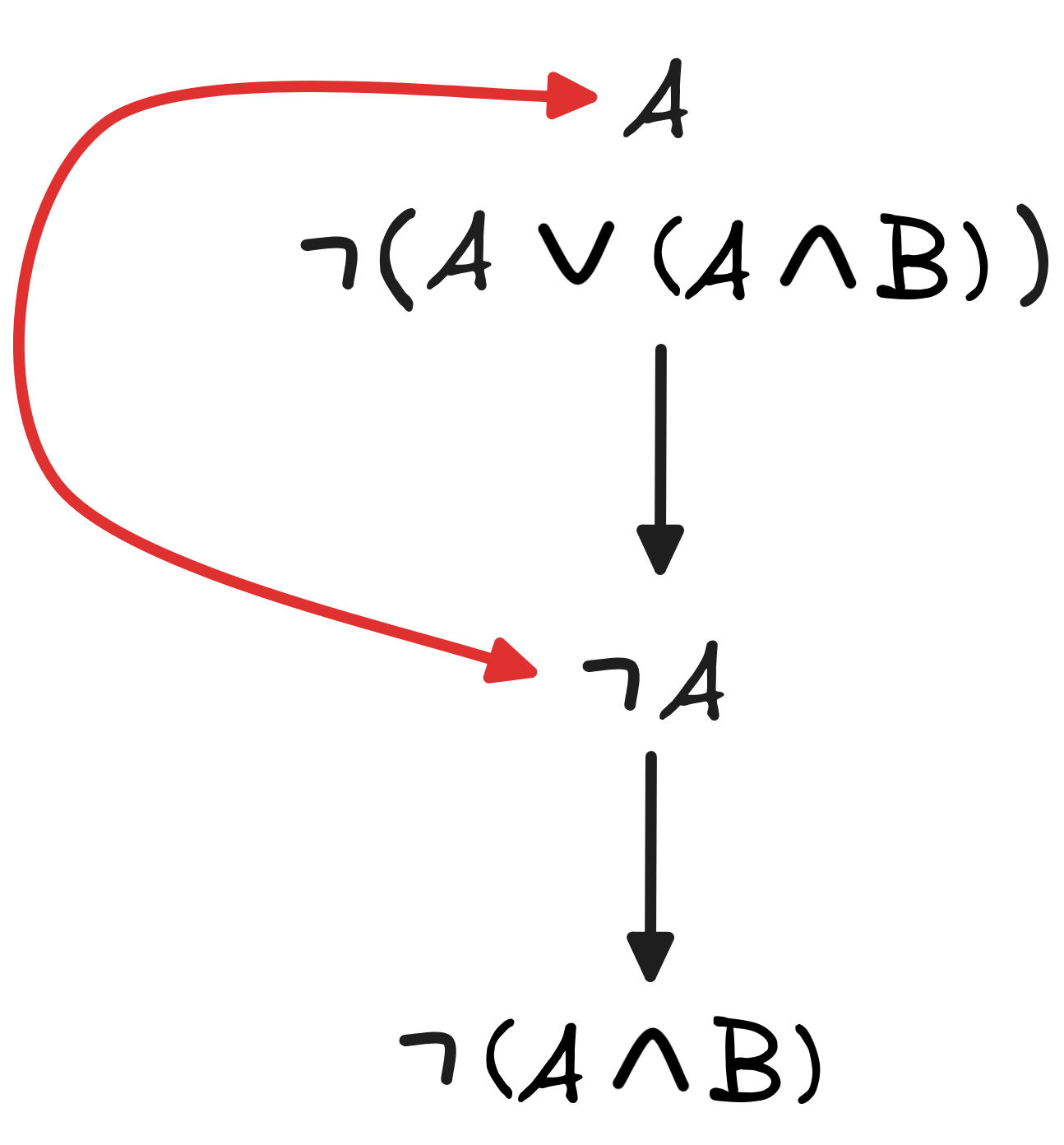
-
A


 A
AThis solution is interactive! Click through the slides to get an explanation of how to find the derivation:
This is perhaps the most difficult one of this set.
-

 A
A
 A
A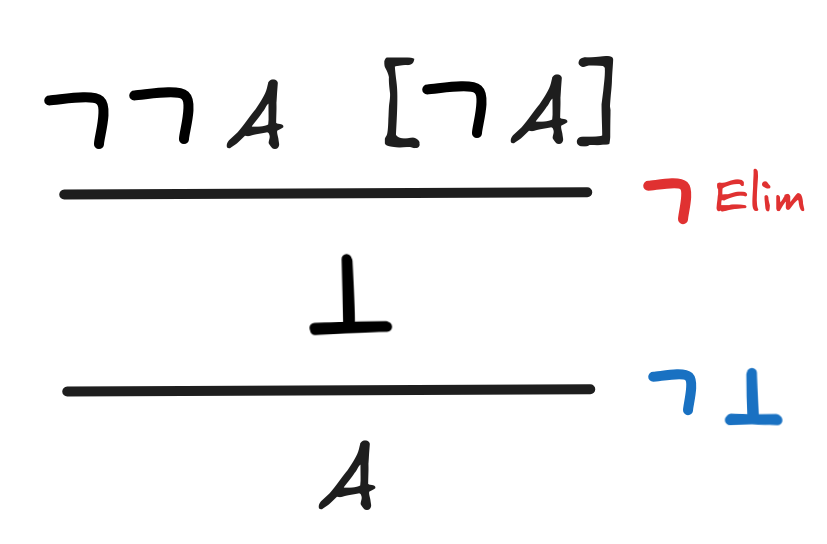
Note that this derivation requires classicality.
-
 (A
(A
 B)
B)

 A
A

 B
B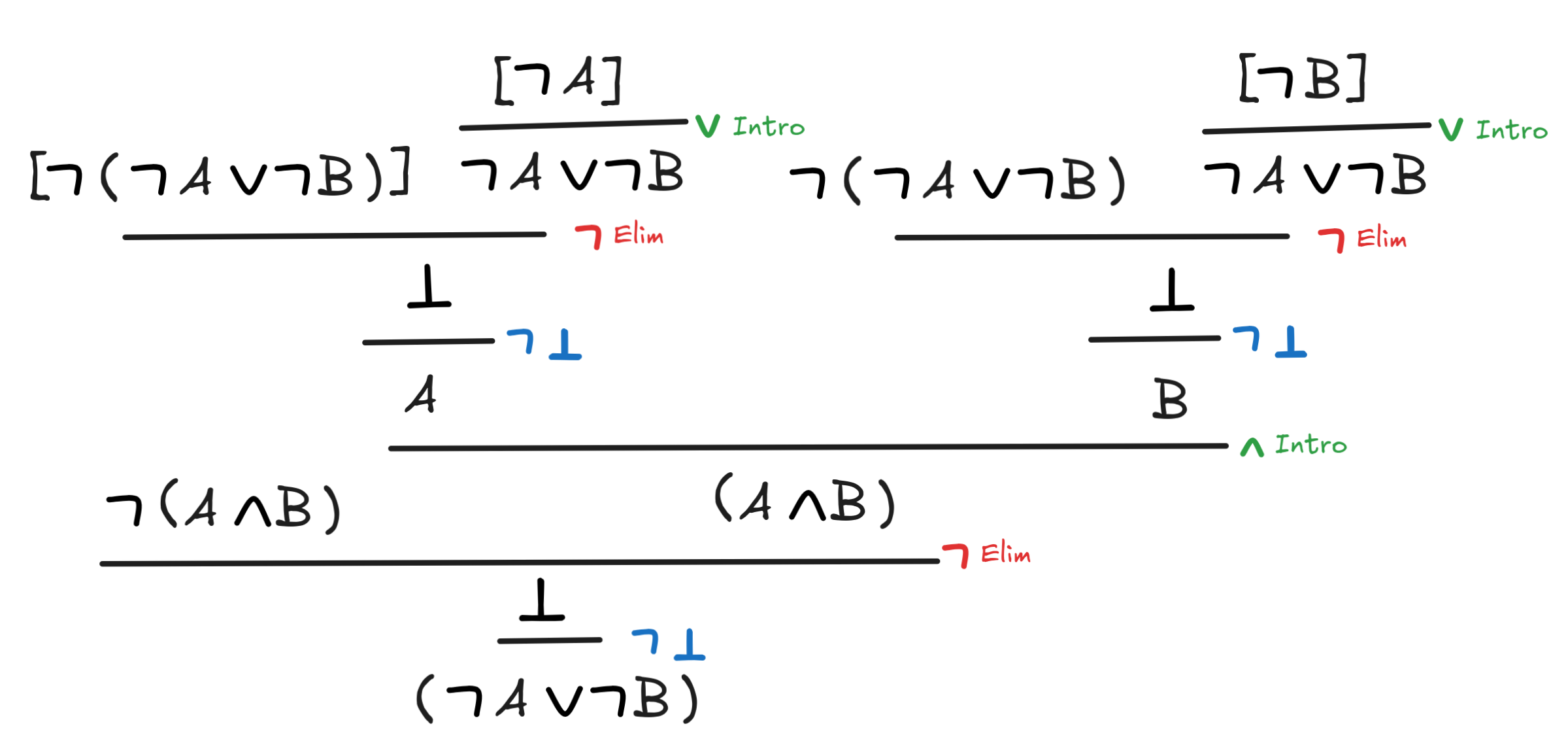
-
 A
A

 B
B

 (A
(A
 B)
B)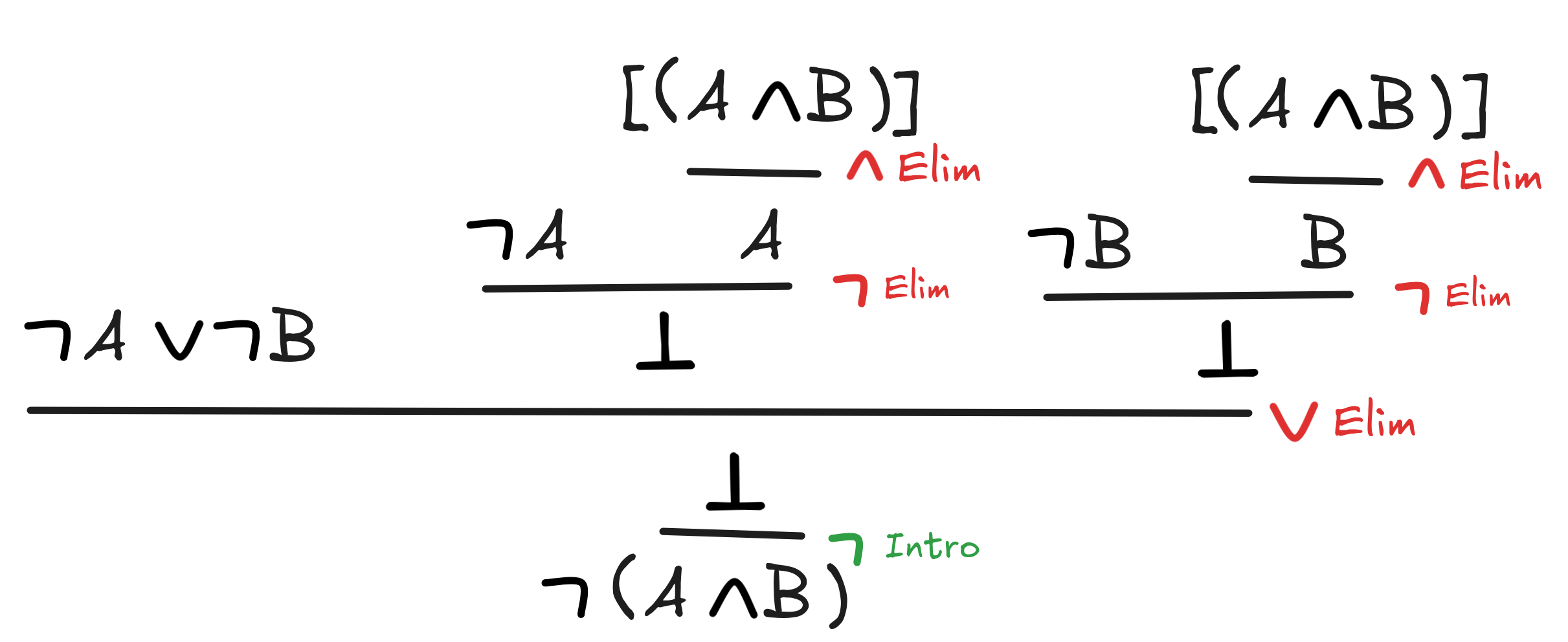
-
 (A
(A
 B)
B)

 A
A

 B
B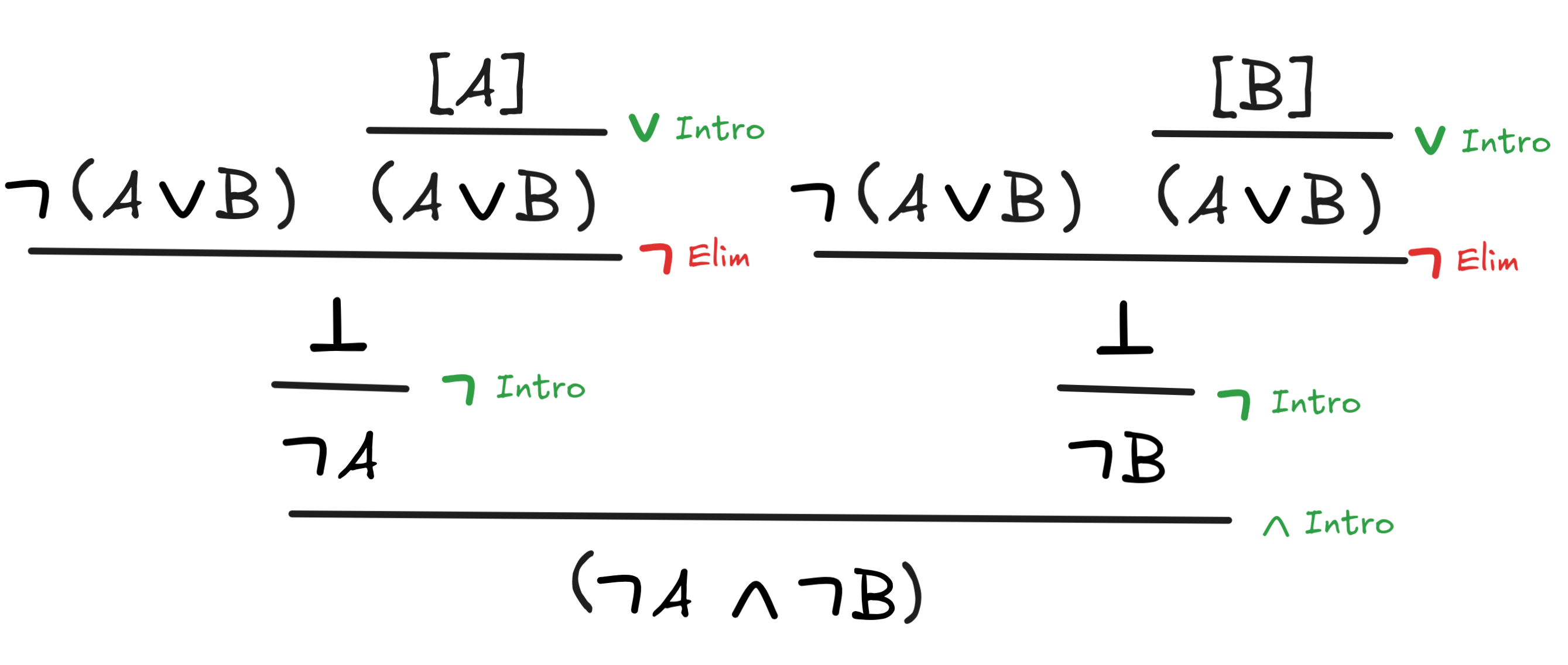
-
 A
A

 B
B

 (A
(A
 B)
B)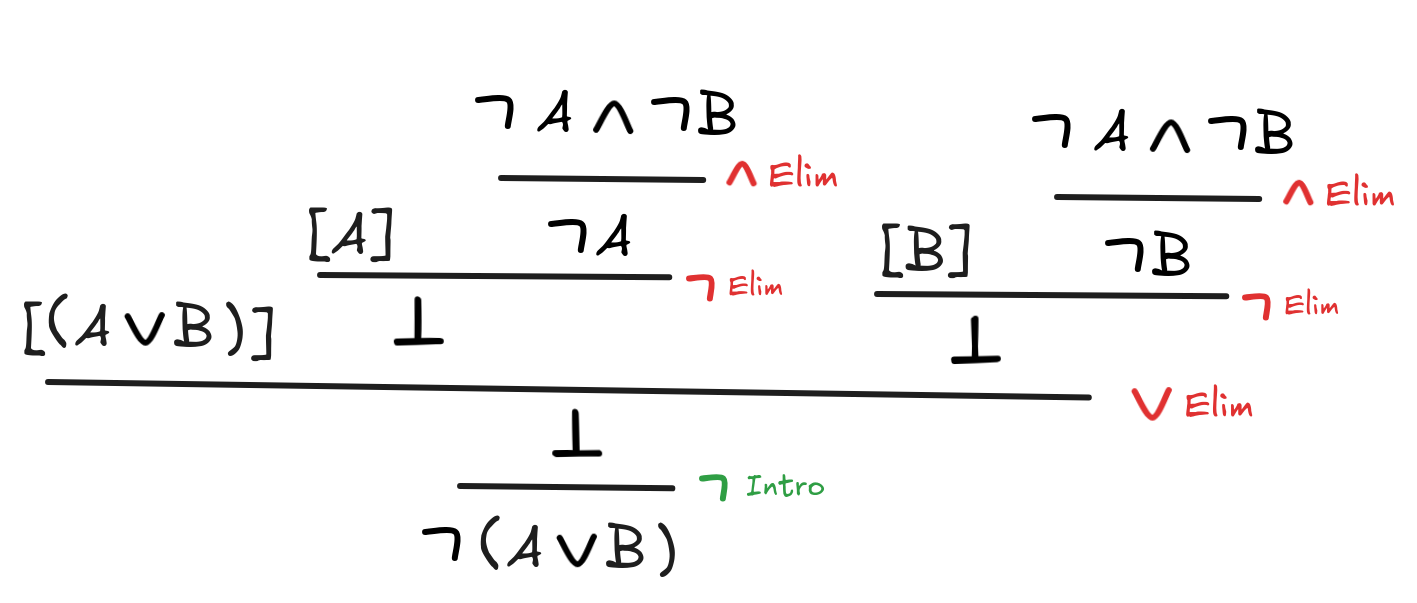
Conditionals
-
 A
A
 B
B
 A
A
 B
BThis solution is interactive! Click through the slides to get an explanation of how to find the derivation:
-
A
 B
B

 A
A
 B
B
-
(
 A
A
 A)
A)
 A
A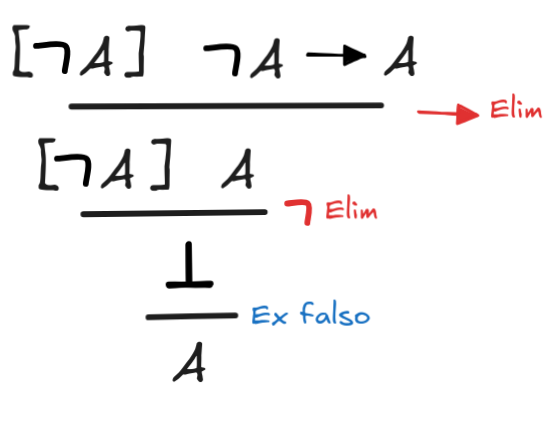
-
(A
 B)
B)
 (
(
 B
B

 A)
A)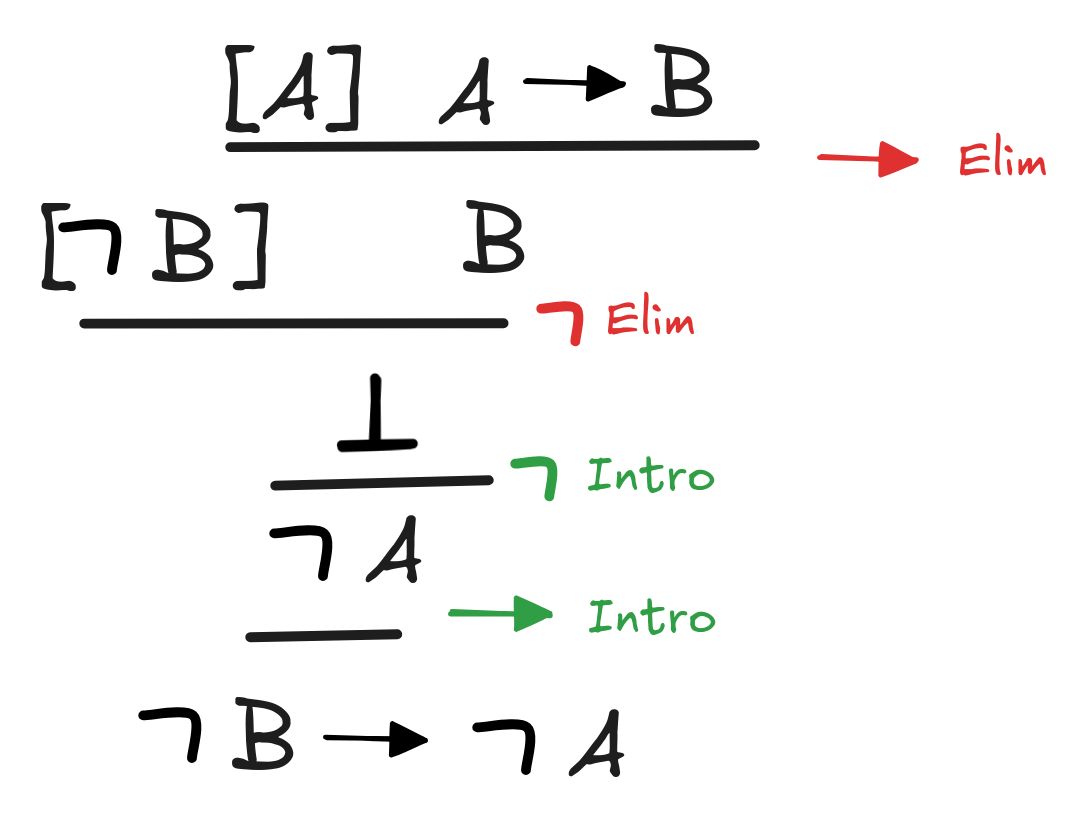
-
(
 B
B

 A)
A)
 (A
(A
 B)
B)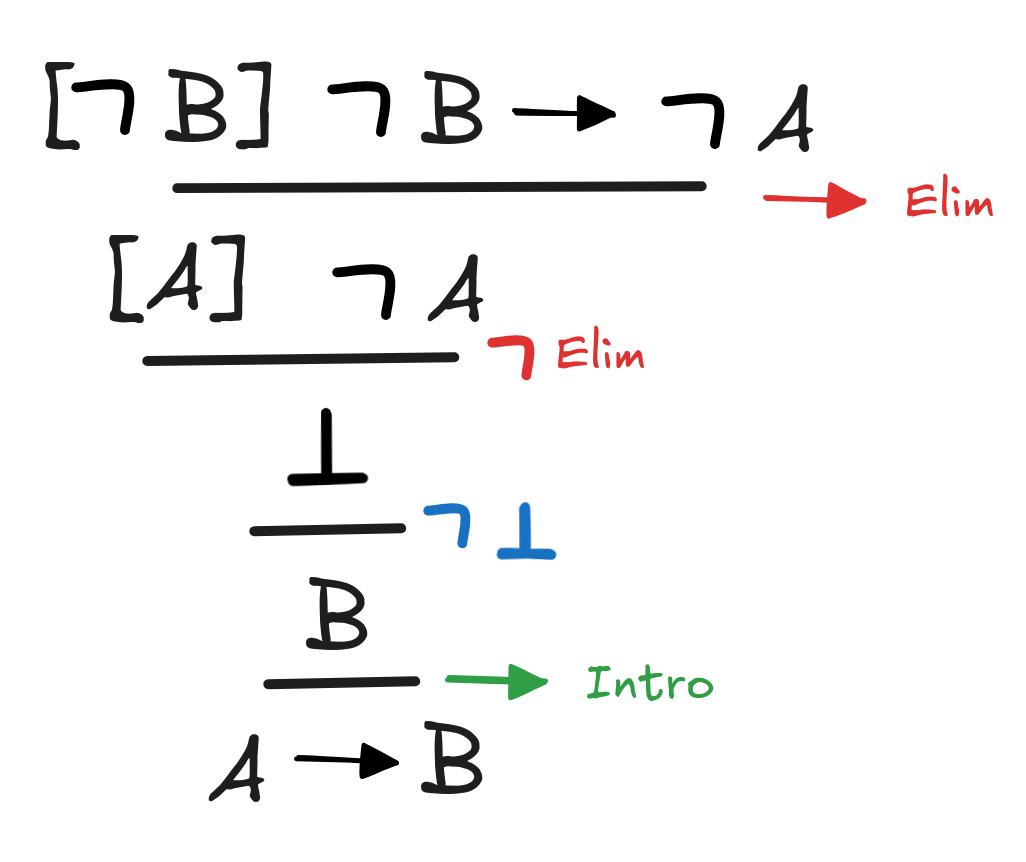
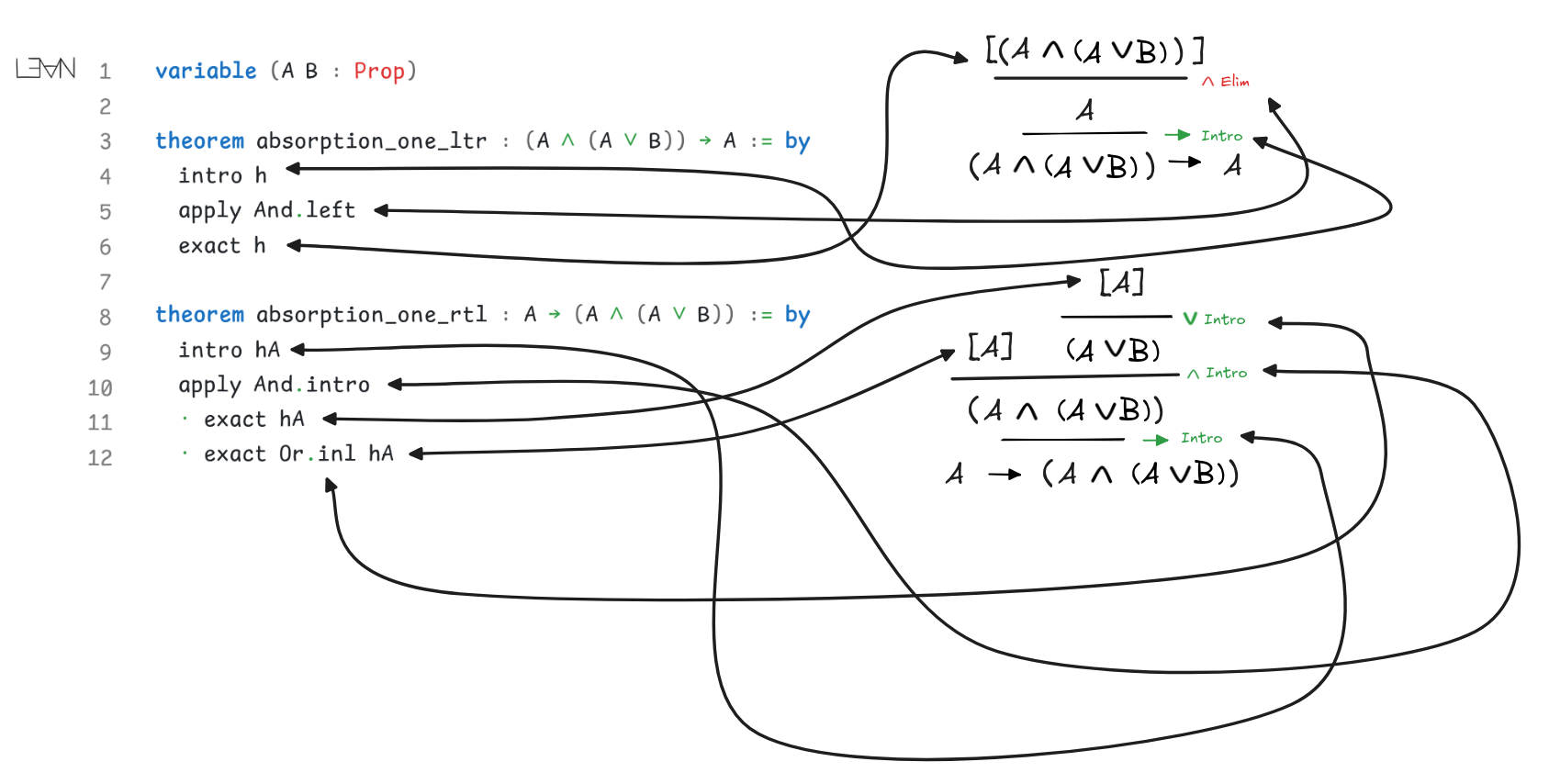
Lean verification
For this exercise, you verify your natural deduction inferences using Lean.
Below are templates for the code to use. The proofs are replaced by sorry, which makes Lean not complain about the missing
proof. The sorry-tactic is very useful when writing a proof, because it makes
Lean “shut up”, while allowing you to type your proof. You need to replace each
sorry with the correct proof, of course.
Note that some of the proofs below require open
Classical. Which ones?
In your proofs, you can use previous theorems using apply. Note that theorem’s
like distribution_one_rtl require to be passed a proof term h.
Conjunction and Disjunction

|
|
Click this link to open the browser playground.
Negation:

|
|
Click this link to open the browser playground.
Conditionals

|
|
Click this link to open the browser playground.
Solution
Credit: Alexander Apers

|
|
You can review the code in the lean plaground by following this link .
Interpreting Lean
Consider the following two Lean proofs. Translate them into natural deduction proofs:

|
|
Click this link to open the browser playground.
Solution