Tutorial 5. Boolean satisfiability
Exercise sheet
Truth-function representations
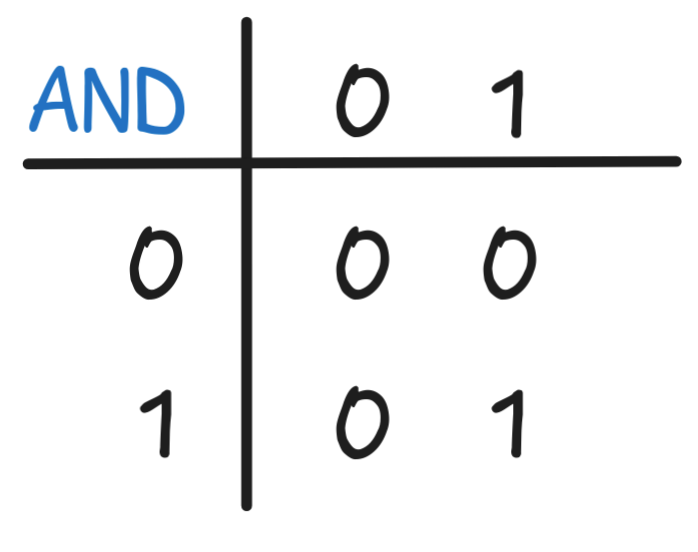
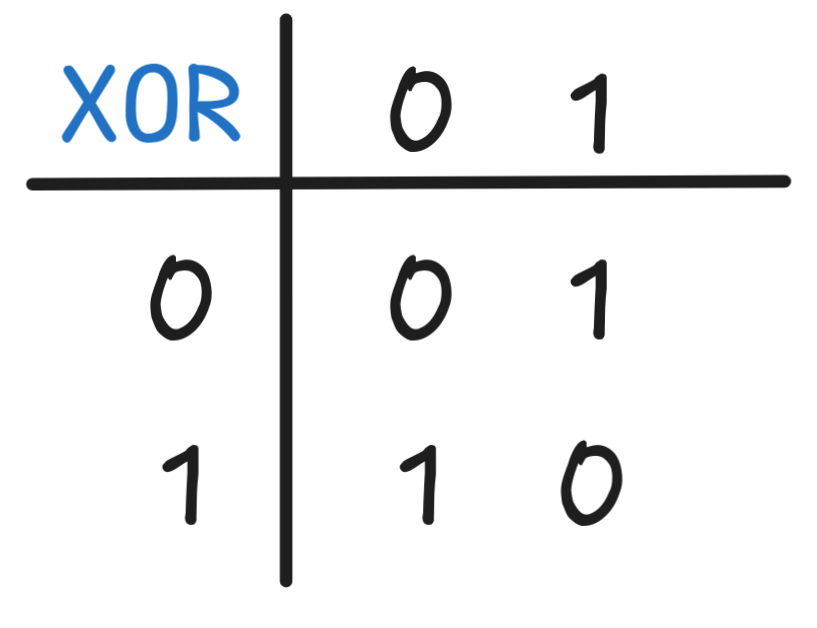
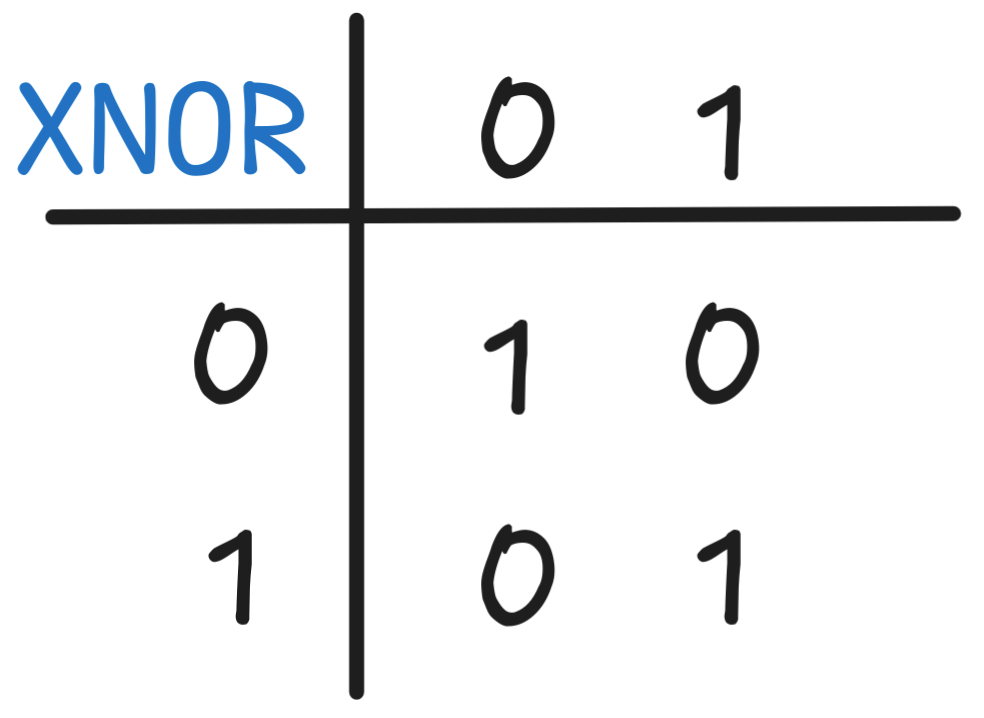
We looked at how to read off a Boolean expression from a truth-table. Apply the method to the following:
|
|
|
|
Inspect the resulting Boolean expressions. Can you simplify them while remaining in DNF?
Solution
-
AND gives us
X AND Y, which cannot be simplified further. -
XOR gives us
(X AND (NOT Y)) OR ((NOT X) AND Y), which cannot be simplified further. -
XNOR gives us
((NOT X) AND (NOT Y)) OR (X AND Y), which cannot be simplified further.
Circuit representations
We’ve observed that our relay circuits are essentially build up from relay implementations of NOT (default “on”) and AND (default “off”). Use the idea to represent the following circuits as Boolean expressions:
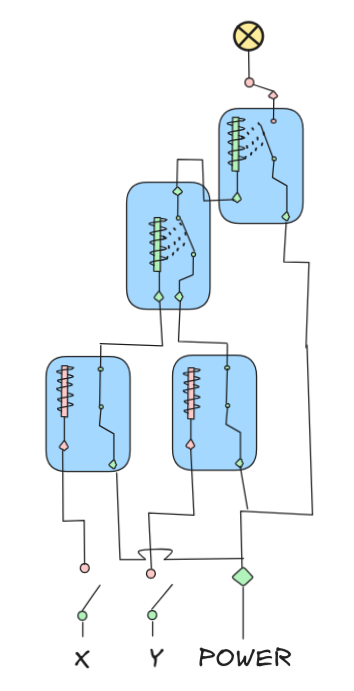
|
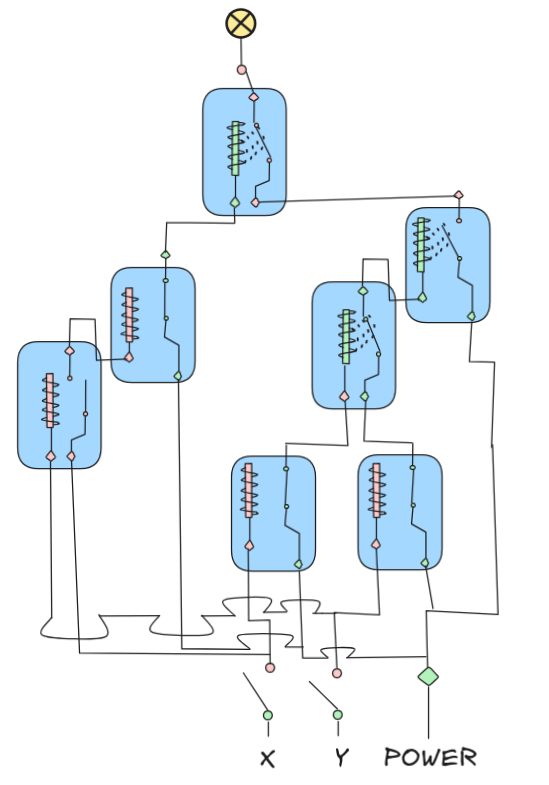
|
Are the resulting formulas in normal form (CNF or DNF)?
Solution
-
The first circuit consist of two NOT’s which are combined with an AND and the output fed into a NOT. That is:
NOT((NOT X) AND (NOT Y))This is an implementation of OR. In fact, the representation is neither in DNF nor CNF and if you transform it, you end up with
X OR Yafter an application of the De Morgan Identities and the law of Double Negation. This is both the DNF and CNF of the representation.
-
The second circuit is a bit more complex. On the right-hand side, we feed both inputs into an AND and apply NOT to the output,
NOT(X AND Y)The right-hand side is actually the first, circuit, which we know corresponds to
NOT((NOT X) AND (NOT Y))The outputs of these two circuits are fed into an AND, which gives us the final representation:
(NOT(X AND Y)) AND (NOT((NOT X) AND (NOT Y)))This formula can be simplified in various ways. One route is via the observation that the first circuit boils down to
X OR Y. This means our circuit is just:(NOT(X AND Y)) AND (X OR Y)Maybe you can already see that this is the XOR function.
Applying De Morgan, we can transform this into the CNF:
((NOT X) OR (NOT Y)) AND (X OR Y)To bring it into DNF, we need to apply Distributivity a bunch of times, but eventually, we can obtain:
(X AND (NOT Y)) OR ((NOT X) AND Y)
Equivalence
The XNOR function is special: it expresses that X and Y have the same value—just check the table!
-
Find the simplest representation of XNOR in terms of NOT and XOR.
Hint: Inspect XNOR and XOR’s function tables, how are they related?
-
Use this implementation to reduce the verification problem for a relay circuit from two
SATproblems for different sets (as in the text) to a singleSATproblem for a single expression.Hint: Think about when
X XNOR Yis true and whenX XOR Yis true.
Solution
-
The simplest representation is
NOT(X XOR Y),that is XNOR is the negation of XOR. You can see this in the table by observing that everywhere the table of XOR has a
1, the table for XNOR has a0, and everywhere XOR is0, XNOR is1. The values are just switched, using NOT.Note that this formula is neither in CNF nor DNF, of course.
-
Suppose we have two Boolean expressions
AandB, which may be complex and use various variables, Boolean operations, etc. We can then check whetherAandBare equivalent by checking whetherA XOR Bis
SAT. Because by the function table for XOR,A XOR B = 1just in case
A = 1andB = 0orA = 0andB = 1, that is, just in case the values ofAandBare different.
Truth tables
Use the truth-table method to check whether the following claims are true:
-
The set of expressions
((NOT X) OR (NOT Y))and(X AND Y)isSAT. -
The set formulas {
 RAIN, (RAIN
RAIN, (RAIN
 (
(
 WIND
WIND
 RAIN) ) } is
RAIN) ) } is SAT.
Solution
-
Here is the complete truth-table:
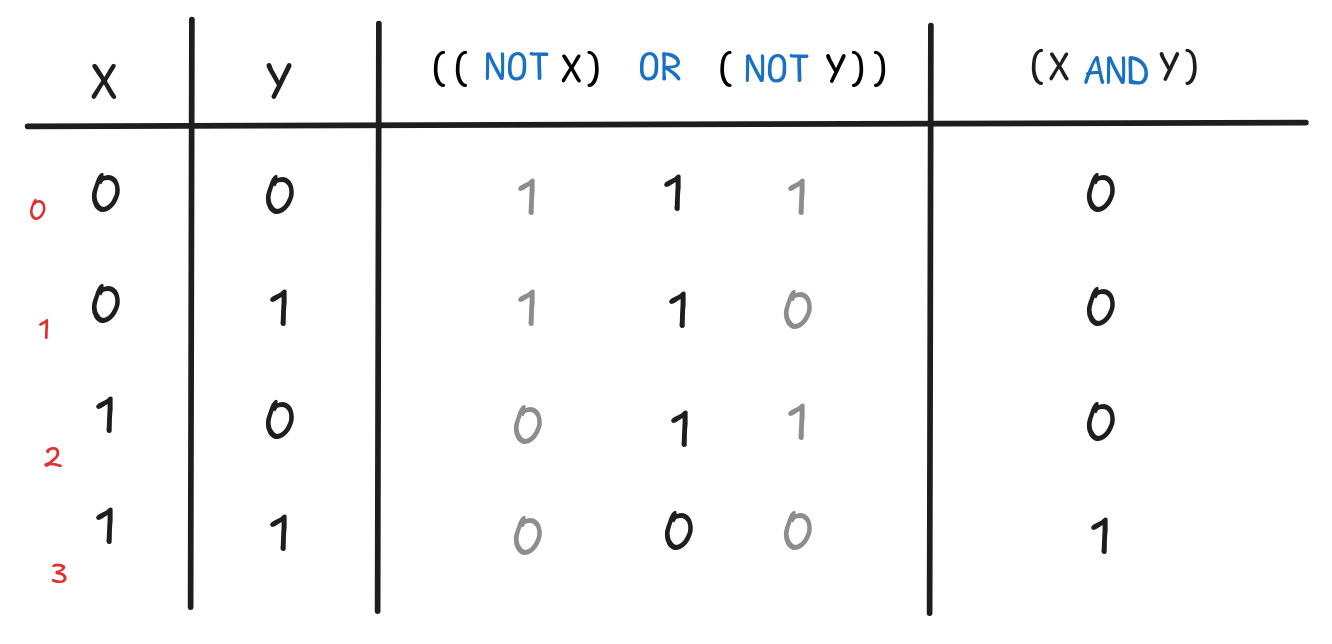
Since there is no row where both expressions have the value
1, the two formulas are not jointly satisfiable. -
Here’s the complete truth-table:
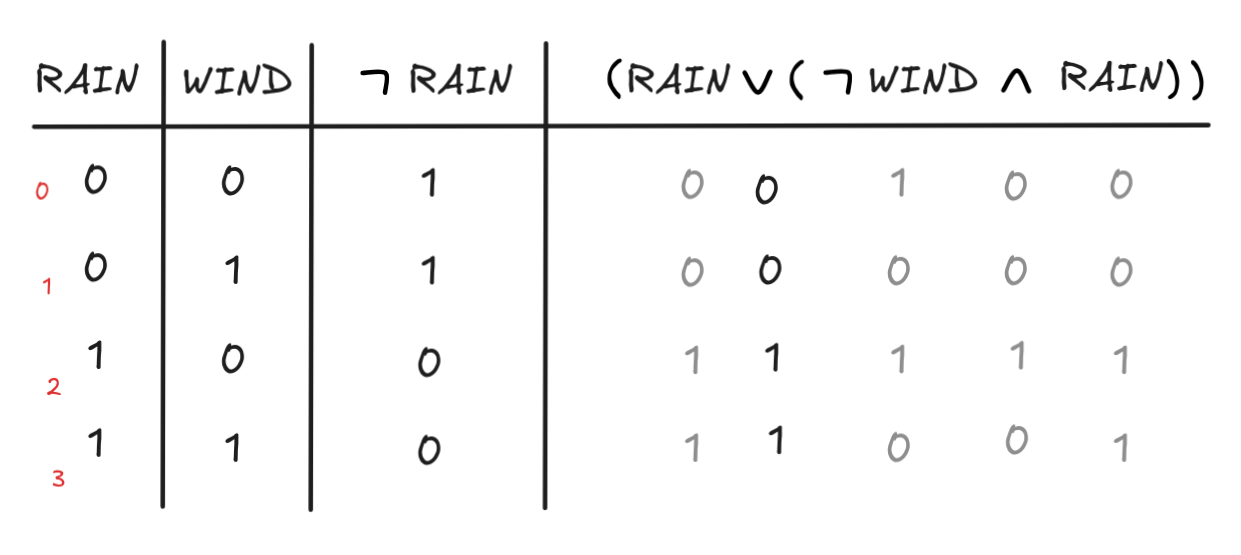
Again, since there is no row where both expressions have the value
1, the two formulas are not jointly satisfiable.
Mystery formula
Determine the following “mystery formula” form its truth-table:
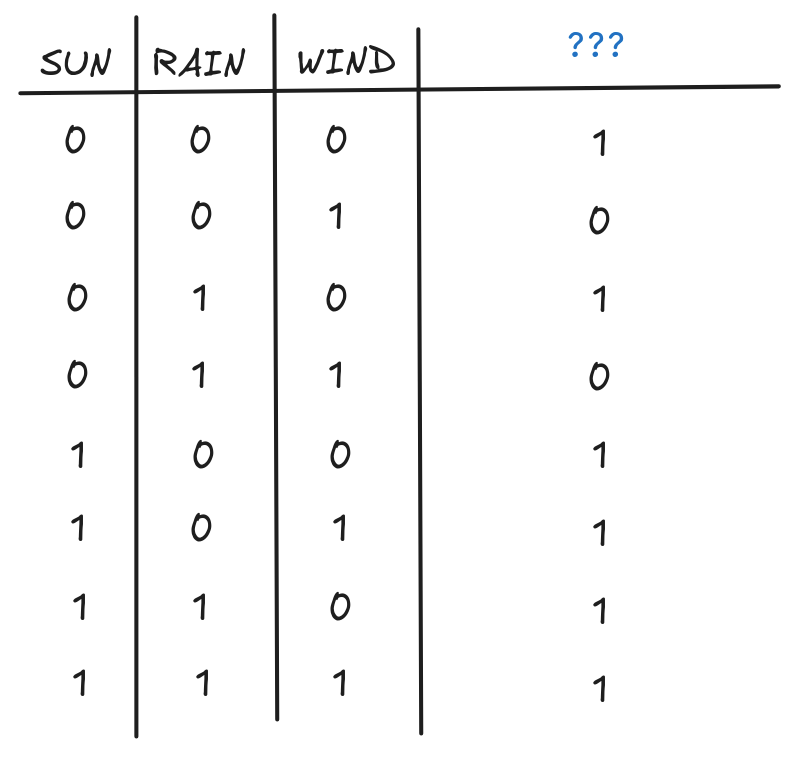
What’s the shortest representation of the formula you can find?
Solution
The “brute force” DNF method yields the following monstrosity:
 SUN
SUN

 RAIN
RAIN

 WIND )
WIND )
 (
(
 SUN
SUN
 RAIN
RAIN

 WIND )
WIND )
 ...
...
 RAIN
RAIN

 WIND )
WIND )
 (SUN
(SUN

 RAIN
RAIN
 WIND )
WIND )
 ...
... RAIN
RAIN

 WIND )
WIND )
 (SUN
(SUN
 RAIN
RAIN
 WIND )
WIND )But if you analyze the truth-table a bit more carefully, then you can notice that in each case where SUN is true, the entire formula is true. And the only other cases where SUN is false and the formula is true are the two cases where WIND is false.
This means that we can equivalently write the formula as:

 WIND
WINDThere are various algorithms for doing these kind of simplifications, an important one of them is to use the Karnaugh map , which is closely related to the Quine-McCluskey algorithm .
Normal Forms
Transform the following formulas into DNF and CNF:
- (RAIN

 (SUN
(SUN

 RAIN))
RAIN)) - (
 RAIN
RAIN

 (
(
 RAIN
RAIN
 WIND))
WIND)) - (RAIN

 SUN)
SUN)
 (
(
 RAIN
RAIN

 SUN)
SUN)
Solution
-
If you apply the rewrite rule r₃ to this formula, you obtain
RAINwhich after one application of r₁ becomes
 SUN
SUN


 RAIN,RAINThis is both the DNF and the CNF of the formula.
RAIN,RAINThis is both the DNF and the CNF of the formula.
 SUN
SUN
 RAIN.
RAIN. -
Here, applying r₃ yields:
An application of r₁ gives RAIN
RAIN
 (
(

 RAIN
RAIN

 WIND).This is the DNF of the formula. To transform it into CNF, we need to apply r₄ to obtain:
WIND).This is the DNF of the formula. To transform it into CNF, we need to apply r₄ to obtain: RAIN
RAIN
 (RAIN
(RAIN

 WIND).
WIND).
 RAIN
RAIN
 RAIN)
RAIN)
 (
(
 RAIN
RAIN

 WIND).
WIND).- This formula is in DNF. We need to apply distribution to get it into CNF. First, with r₄ we get: ((RAINThen, applying r₄’ twice, we get:

 SUN)
SUN)

 RAIN)
RAIN)
 ((RAIN
((RAIN

 SUN)
SUN)

 SUN).(RAINwhich is the formula’s CNF.
SUN).(RAINwhich is the formula’s CNF.
 RAIN)
RAIN)
 (
(
 SUN
SUN

 RAIN)
RAIN)
 (RAIN
(RAIN

 SUN)
SUN)
 (
(
 SUN
SUN

 SUN),
SUN),
Resolution
Use the resolution method to determine whether the following formulas are satisfiable:
- (SUN
 RAIN
RAIN

 WIND)
WIND)
 (SUN
(SUN

 RAIN
RAIN

 WIND)
WIND) -
 (SUN
(SUN
 RAIN)
RAIN)
 (WIND
(WIND

 WIND)
WIND) - (SUN
 RAIN)
RAIN)
 (SUN
(SUN

 RAIN)
RAIN)
 (
(
 SUN
SUN
 RAIN)
RAIN)
 (
(
 SUN
SUN

 RAIN)
RAIN) - (SUN
 (SUN
(SUN
 RAIN))
RAIN))
 (RAIN
(RAIN
 (RAIN
(RAIN
 SUN))
SUN))
Solution
-
The formula is already in CNF, so we can directly transform it into sets to obtain:
{ SUN, RAIN,There is one possible application of resolution (eliminating RAIN and WIND } { SUN,
WIND } { SUN,
 RAIN,
RAIN,
 WIND }.
WIND }. RAIN), which yields { SUN,Since there are no more resolutions possible and we haven’t derived { }, we conclude that the formula is satisfiable. E.g. by setting v(SUN) = 1.
RAIN), which yields { SUN,Since there are no more resolutions possible and we haven’t derived { }, we conclude that the formula is satisfiable. E.g. by setting v(SUN) = 1. WIND }.
WIND }. -
This formula, we need to transform into CNF first. Applying r₂, we obtain:
(An application of r₄ gives us from that: SUN
SUN

 RAIN)
RAIN)
 (WIND
(WIND

 WIND).(Now, we can translate to sets to get:
WIND).(Now, we can translate to sets to get: SUN
SUN

 RAIN
RAIN
 WIND)
WIND)
 (
(
 SUN
SUN

 RAIN
RAIN

 WIND).{But just one resolution is possible, which eliminates WIND and
WIND).{But just one resolution is possible, which eliminates WIND and SUN,
SUN,
 RAIN , WIND} {
RAIN , WIND} {
 SUN,
SUN,
 RAIN,
RAIN,
 WIND}.
WIND}. WIND to give us: {Since there are no more resolutions possible and we haven’t derived { }, we conclude that the formula is satisfiable. E.g. by setting v(SUN) = 0.
WIND to give us: {Since there are no more resolutions possible and we haven’t derived { }, we conclude that the formula is satisfiable. E.g. by setting v(SUN) = 0. SUN,
SUN,
 RAIN }.
RAIN }. -
This formula is in CNF, so we directly go to the sets:
{ SUN, RAIN } {SUN,The following is a derivation of { } from these using resolution: RAIN} {
RAIN} {
 SUN, RAIN} {
SUN, RAIN} {
 SUN,
SUN,
 RAIN}.
RAIN}.
Note that we needed to use { SUN }, which was the result of the first resolution again in the last resolution. This is why it’s important to recursively resolve, meaning adding the results of the resolutions to our base and keep resolving until we can’t anymore.
The conclusion is that the formula is unsatisfiable.
-
This formula is in CNF, so we can directly go to the sets:
{ SUN } { SUN, RAIN } { RAIN } { RAIN, SUN }But since there are no ’s in this, we can not resolve and conclude that the formula is satisfiable, simply by setting v(SUN) = v(RAIN) = 1.
’s in this, we can not resolve and conclude that the formula is satisfiable, simply by setting v(SUN) = v(RAIN) = 1.
Valid inference
Determine whether the following inferences are valid using both the truth-table and the resolution method. Which one is faster?
-
 RAIN
RAIN
 RAIN
RAIN
 (
(
 RAIN
RAIN
 SUN)
SUN) -
RAIN
 (RAIN
(RAIN
 WIND)
WIND)
 RAIN
RAIN
 SUN
SUN
Solution
-
To check whether the inference is valid, we need to check whether
Here’s how the truth-table method shows that the set isSAT{ RAIN,
RAIN,
 (RAIN
(RAIN
 (
(
 RAIN
RAIN
 SUN))}.
SUN))}.SAT: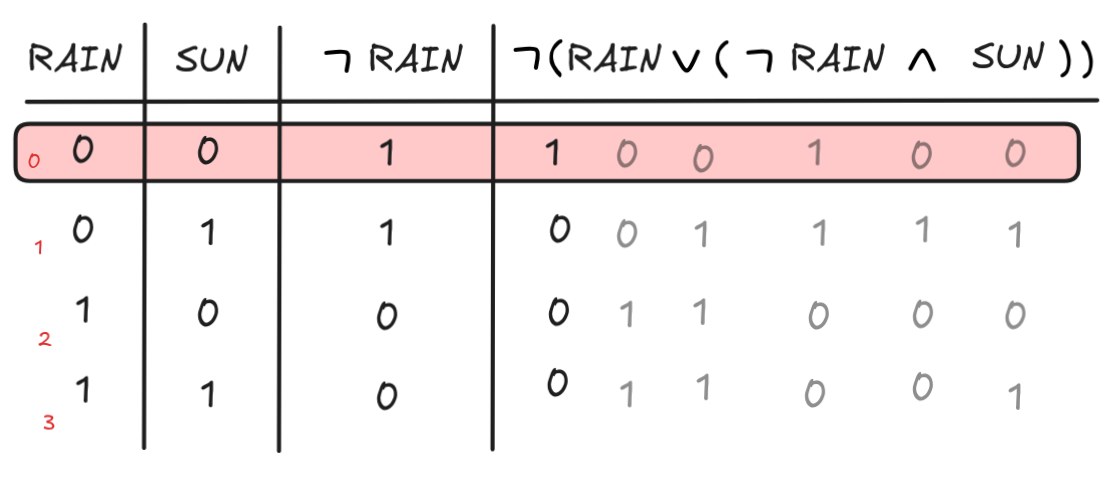
The red row shows that there’s a model where the premise is true and the conclusion false, thus the inference is invalid.
To apply the resolution method, we first need to bring both formulas into CNF.
 RAIN already is in CNF, so we focus on
RAIN already is in CNF, so we focus on
 (RAIN
(RAIN
 (
(
 RAIN
RAIN
 SUN)) and apply r₃ to obtain:A following application of r₂ yields:
SUN)) and apply r₃ to obtain:A following application of r₂ yields: RAIN
RAIN

 (
(
 RAIN
RAIN
 SUN)).Finally, applying r₁ gives us the CNF:
SUN)).Finally, applying r₁ gives us the CNF: RAIN
RAIN
 (
(

 RAIN
RAIN

 SUN)).
SUN)). RAIN
RAIN
 (RAIN
(RAIN

 SUN)).
SUN)).We obtain the sets:
{Note that { RAIN } { RAIN,
RAIN } { RAIN,
 SUN }
SUN } RAIN } is already there. One application of
resolution eliminates RAIN and
RAIN } is already there. One application of
resolution eliminates RAIN and
 RAIN, giving us the set
{
RAIN, giving us the set
{
 SUN}. Since we cannot resolve any further, we conclude the
set is satisfiable and the inference thus invalid. We can read off the same
counter-model as before, if we so desire.
SUN}. Since we cannot resolve any further, we conclude the
set is satisfiable and the inference thus invalid. We can read off the same
counter-model as before, if we so desire.
Comparison in terms of speed on this abstract level are tricky, but one way to compare the two is how many operations we needed to carry out. The truth-table method required us to generate 4 valuations and carry out 7 Boolean calculations each. That is a total 4 + (4 x 7) = = 32 operations. We were lucky that the first row yielded the correct answer, so we only needed to carry out 32 + 1 = 33 operations to obtain the correct result.
For the resolution method, the main bottle neck is the transformation into CNF. Here, it took 3 steps. Add to this the single resolution step and 2 checks for possible further resolutions, this leaves us with a grand total of 3 + 1 + 2 = 6 steps.
Of course, a real comparison in terms of speed depends on a lot of implementation details: how we enumerate the valuations, calculate the Boolean operations, recursively re-write formulas, check for resolvability, etc. In fact, we can imagine a smarter implementation of the truth-table method, where rather than first generating all the rows and columns and then checking, we first generate each row and then check whether it’s a countermodel and only continue if it isn’t. In this case, this would provide a speed-up, where we only need to generate one row, carry out 7 Boolean calculations, and do a final check. Since Boolean operations are fairly “low-level”—certainly lower level than recursive rewrites—it’s plausible that this smarter truth-table algorithm could outperform resolution in real world use-cases. In fact, there are various smarter ways of implementing truth-tables.
But note that this depends on the counter-example occurring “early” in our truth-table, here in the first row. If the counter-example happens later in the table, or not at all because the inference is valid, resolution has a good chance to outperform truth-tables.
-
To check whether the inference is valid, we need to check whether
Here’s the truth-table showing the unsatisfiability of the set:SAT{ RAIN (RAIN
(RAIN
 WIND),
WIND),
 (RAIN
(RAIN
 SUN)}
SUN)}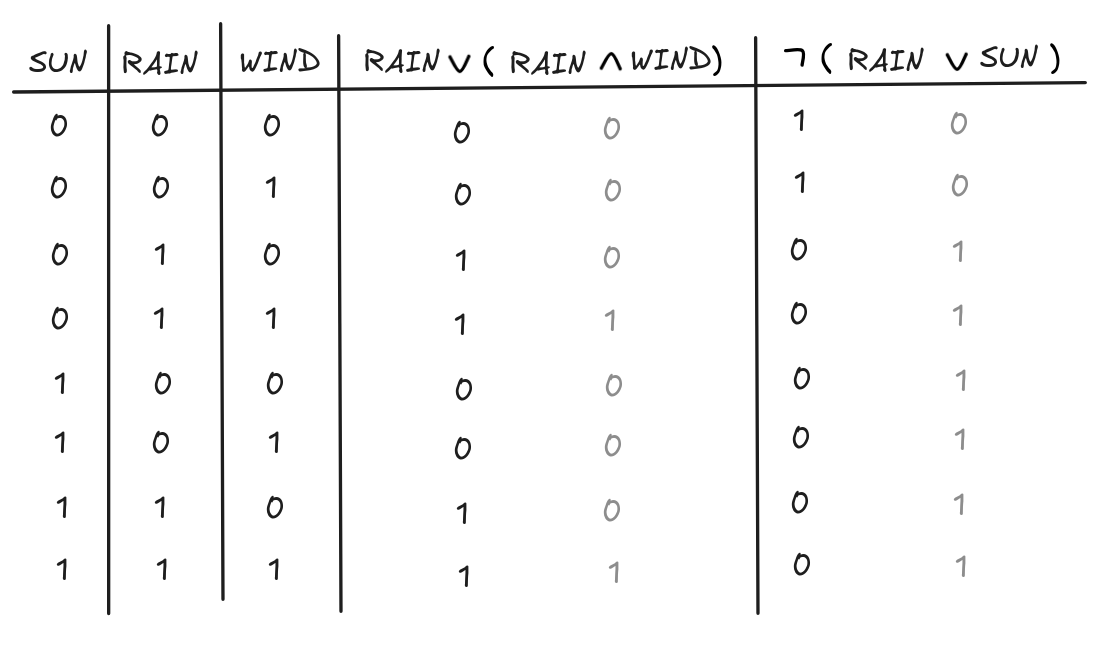
Note that we need to generate the full truth-table to see that there are no counter-examples.
Resolution, instead, is much faster. First, we bring both formulas into CNF:
-
RAIN
 (RAIN
(RAIN
 WIND) requires one distribution r₄
to become (RAIN
WIND) requires one distribution r₄
to become (RAIN
 RAIN )
RAIN )
 (RAIN
(RAIN
 WIND).
WIND). -
 (RAIN
(RAIN
 SUN) requires one De Morgan re-write using
r₂, giving us the CNF
SUN) requires one De Morgan re-write using
r₂, giving us the CNF
 RAIN
RAIN

 SUN
SUN
The resulting set clauses are:
{ RAIN } { RAIN, WIND } {A single application of resolution on { RAIN } and { RAIN} {
RAIN} {
 SUN}.
SUN}. RAIN} derives the empty
set { }, showing the unsatisfiability of the set, and thus validity of
the inference.
RAIN} derives the empty
set { }, showing the unsatisfiability of the set, and thus validity of
the inference.
-