Lecture 12. Logical learning
Slides∀I
Logical methods for AI
Lecture 12
Logical learning
This work is licensed under CC BY 4.0
-
Logic-based learning
Aim
- For last lecture: learning
- We understand this today as: how to respond to new facts.
- There are other concepts of logical learning, e.g. "data fitting."
- Some overlap.
Aim
- Two models:
- Deductive: belief revision
- Inductive: Bayesian updating
-
Belief revision
Setup
- Knowledge base: $\mathsf{KB}\subseteq \mathcal{L}$
- Deductive closure: $\mathsf{KB}\vDash A\Rightarrow A\in KB$
- Learn new fact: $A\notin \mathsf{KB}$. $$\text{Say}: \mathsf{RAIN}\notin\mathsf{KB}$$
- What to do?
Easy: no conflict
$$\neg\mathsf{RAIN}\notin\mathsf{KB}$$- Simply add $\mathsf{RAIN}$.
- $\mathsf{KB}+A=\Set{B:\mathsf{KB},A\vdash B}$
- Conservative: $$\mathsf{KB},A\vdash \mathsf{KB}$$ $$\mathsf{KB},A\vdash A$$
Harder: conflict
$$\neg\mathsf{RAIN}\in\mathsf{KB}$$- Problem: $\mathsf{KB}+\mathsf{RAIN}$ is inconsistent.
- Idea: "remove" $\neg\mathsf{RAIN}$.
- First approach: $$\mathsf{KB}-\neg A = \Set{B\in\mathsf{KB}:B\text{ not eqv. to }\neg A}$$ $$(\mathsf{KB}-\neg A)+A?$$
Problem
- Suppose: $$\mathsf{HIGH\_PRESSURE}\in\mathsf{KB}$$ $$\mathsf{WARM}\in\mathsf{KB}$$ $$\mathsf{HIGH\_PRESSURE}\land\mathsf{WARM}\to\neg\mathsf{RAIN}\in\mathsf{KB}$$
- Then: $$(\mathsf{KB}-\neg\mathsf{RAIN})+\mathsf{RAIN}\vdash \neg\mathsf{RAIN}$$
Worse
- By closure: $$\neg\mathsf{RAIN}\vdash \neg\mathsf{RAIN}\lor \bot\in\mathsf{KB}$$ $$\neg\mathsf{RAIN}\in\mathsf{KB}\Rightarrow\neg\mathsf{RAIN}\lor \bot\in\mathsf{KB}$$
- So: $$(\mathsf{KB}-\neg\mathsf{RAIN})+\mathsf{RAIN}\vdash \bot$$
- Even if we solved the first problem.
What to do?
- Which "grounds" to remove? $$\mathsf{HIGH\_PRESSURE}\in\mathsf{KB}$$ $$\mathsf{WARM}\in\mathsf{KB}$$ $$\mathsf{HIGH\_PRESSURE}\land\mathsf{WARM}\to\neg\mathsf{RAIN}\in\mathsf{KB}$$
- Which consequences to remove?
AGM Axioms
- $\mathsf{KB}\ast A$ is always deductively closed
- $A\in \mathsf{KB}\ast A$
- $\mathsf{KB}\ast A\subseteq \mathsf{KB}+A$
- If $\neg A\notin\mathsf{KB}$, then $\mathsf{KB}\ast A=\mathsf{KB}+A$
- $\mathsf{KB}\ast A$ is only inconsistent if $A$ itself is
- If $A,B$ are logically equivalent, then $\mathsf{KB}\ast A=\mathsf{KB}\ast B$
- $\mathsf{KB}\ast(A\land B)\subseteq (\mathsf{KB}\ast A)+B$
- If $\neg B\notin\mathsf{KB}\ast A$, then $(\mathsf{KB}\ast A)+B\subseteq \mathsf{KB}\ast(A\land B)$
Outlook
- Aim: define revision operator $\ast$.
- Problem: many different options.
- "Best" revision depends on the world, subject matter, $KB$-external knowledge, ...
-
Bayesian updating
Setup
- Knowledge base: $Pr_\mathsf{KB}:\mathcal{L}\to\mathbb{R}$
- Learn new fact $A$: $Pr_\mathsf{KB}(A)\neq 1$.
- "Learnable" fact: $Pr_\mathsf{KB}(A)\neq 0$.
- What now?
Solution
$$Pr_{\mathsf{KB}\ast\mathsf{RAIN}}(\ \cdot\ )=Pr_\mathsf{KB}(\ \cdot \mid \mathsf{RAIN})$$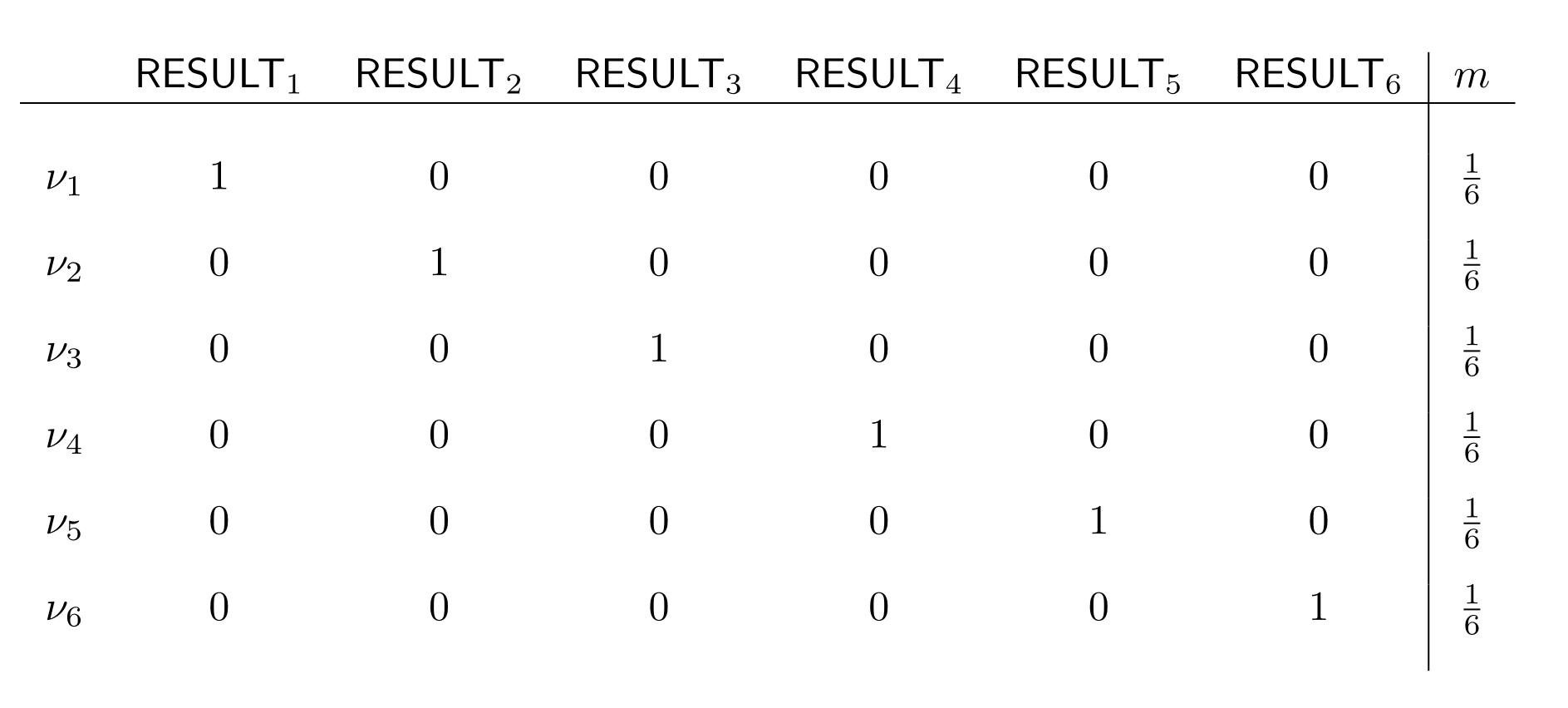
$$\text{Learn}: \mathsf{RESULT}_2\lor\mathsf{RESULT}_4\lor \mathsf{RESULT}_6?$$
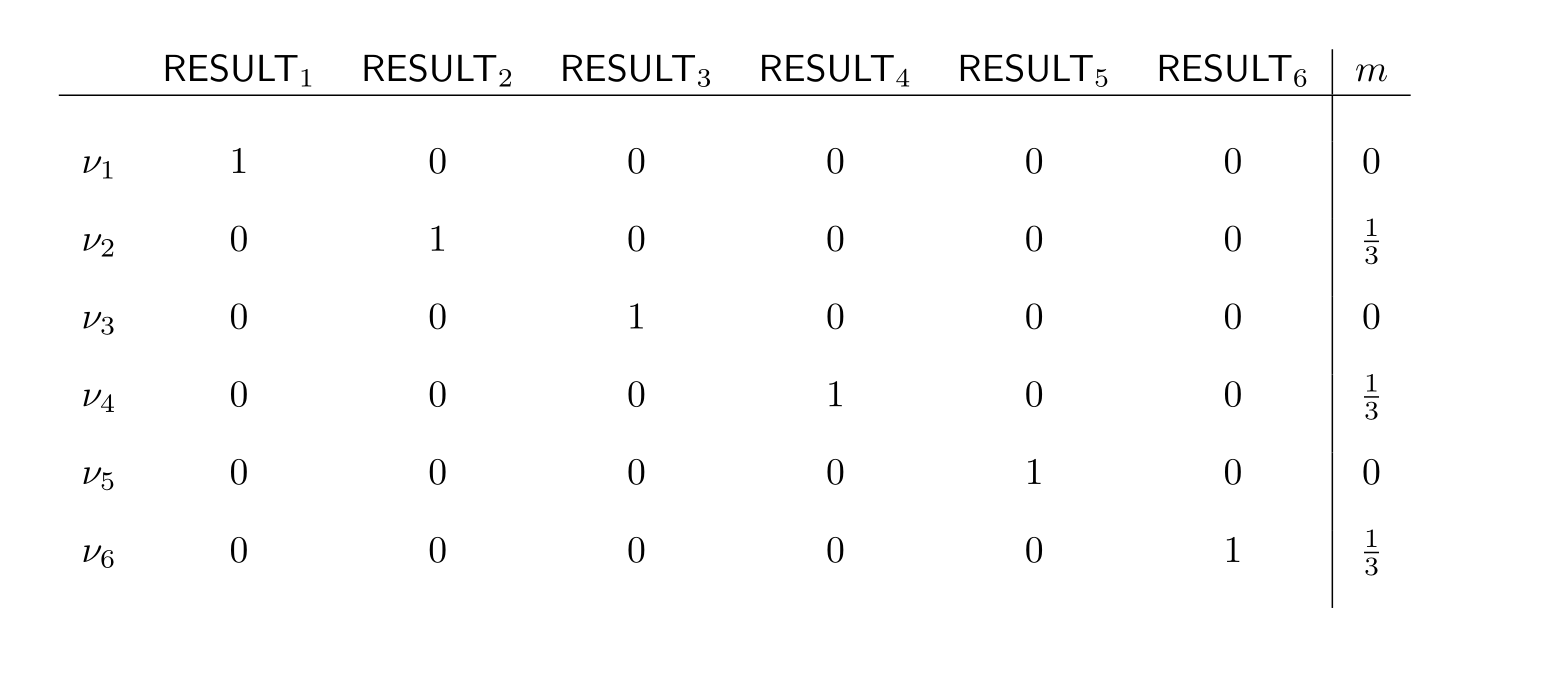
Bayes rule
$$Pr(A\mid B)=\frac{Pr(B\mid A)\times Pr(A)}{Pr(B)}$$- $Pr(A\mid B)$ is the posterior probability
- $Pr(A)$ is called the prior probability
- $Pr(B)$ is called the marginal probability
- $Pr(B\mid A)$ is called the likelihood
Example
$$\mathbf{Marginal}: Pr_\mathsf{KB}(\mathsf{RAIN})=0.25$$ $$\mathbf{Likelihood}: Pr_\mathsf{KB}(\mathsf{RAIN}\mid \mathsf{HIGH\_PRESSURE})=0.2$$ $$\mathbf{Prior}: Pr_\mathsf{KB}(\mathsf{HIGH\_PRESSURE})=0.8$$ $$\mathbf{Posterior}: Pr(\mathsf{HIGH\\_PRESSURE}\mid\mathsf{RAIN})$$ $$=\frac{Pr(\mathsf{RAIN}\mid \mathsf{HIGH\_PRESSURE})\times Pr(\mathsf{HIGH\_PRESSURE})}{Pr(\mathsf{RAIN})}$$ $$=\frac{0.2\times0.8}{0.25}=0.64$$Applications
- From text recognition to spam filters.
- Not efficient: need to recalculate all probabilities every time.
-
Conclusion
Conclusion
- Three roles of logic:
- Foundational
- Methodological
- As a tool
- Not the main method (anymore), but everywhere.
- You now know how this works, abstractly.
Thanks!
Highlights
Powered by
