First-Order Logic

First-order logic (FOL) is one of the most powerful logical systems in common use today. Part of its strength derives from its expressive power: it’s ability to express complex ideas in syntactically straightforward and logically tractable ways. In fact, FOL-style syntax is the effective paradigm in which most of modern mathematics, physics, economics, and other formal theories are formulated.

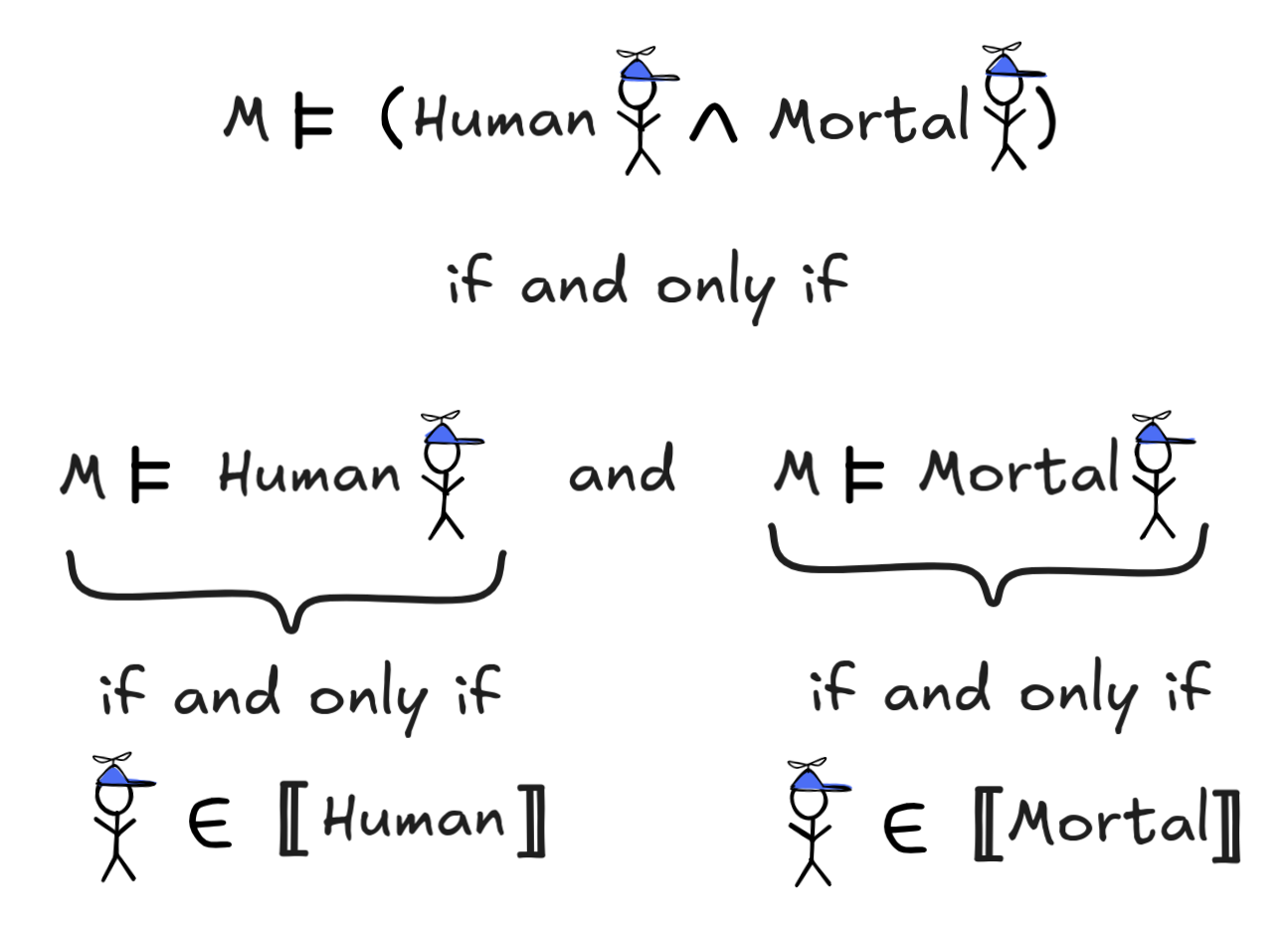
This makes reasoning in FOL a natural target for AI research into automated reasoning techniques, proof verification, etc. And, in fact, we’ll be looking at these topics in the next chapter. In this chapter, we’ll explore an even deeper connection between FOL and AI, which has to do with the way we formalize and store knowledge. We’ve already explored the idea of KBs, which are sets of formulas that we use to represent knowledge about the world. When we’re using propositional logic, these representations are typically rather simplistic, which has to do with the lack of expressive power in propositional logic.

For example, propositional logic doesn’t have the expressive power to properly capture the content of “all humans are mortal” from our paradigmatic deductive inference:

All humans are mortal, Socrates is human Socrates is mortal

What we can write in propositional logic is something like

HUMAN MORTAL

which expresses a rule-like connection between being human and being mortal. But what’s lacking here is the idea that this is a connection that holds for all humans, and so Socrates in particular. FOL has syntactic devices to express this kind of generality, the so-called “quantifiers”,   (read: “for all”) and   (read “exists”). The standard way to represent the claim that all humans are mortal in FOL is something like the following formula:

x(Human x Mortal x)

This formula says that any arbitrary object, x, if it has the property of being human, then it has the property of being mortal. This general formula we can particularize to Socrates by taking it’s instance:

Human(Socrates) Mortal(Socrates)

Then, adding the additional premise that Mortal(Socrates), we can perform our desired inference using MP. Crucially, however, we can do this for anything whatsoever:

• All humans are mortal, Ada Lovelace is human Ada Lovelace is mortal
• All humans are mortal, Alan Turing is human Alan Turing is mortal
• …

When analyzed in FOL these inferences use the same representation of the fact that all humans are mortal, viz.: x(Human x Mortal x).

The increase in expressive power from propositional logic to FOL is immense. In fact, FOL can express almost any kind of fact about the world we’d want to include in our KB in a straight-forward and logically tractable fashion. Historically, the need for the expressive power was first noticed in mathematics, where it became apparent in the 19th century that the rigorous, axiomatic treatment of basic concepts like continuity required quantifiers. But today, we make use of this expressive powers in virtually all contexts where we have to store information in databases. As it turns out, FOL is the logical foundation for database theory.

That is, from a logical perspective, we can look at databases (DBs) as a special form of FOL models, where querying a database—automatically retrieving information from it—ultimately boils down to interpreting FOL formulas in DBs. This is, effectively, the content Codd’s theorem, which makes FOL one of the most important logical tools for AI: it’s the way we interact with KBs and, more generally, DBs. And this is not only an academic curiosity. As you’ll see in this chapter, FOL is the ultimate logical basis for some of the most important and widely used query languages, such as SQL.

At the end of this chapter, you will be able to:

• define FOL languages and parse FOL formulas
• explain the concept of an FOL model
• determine the objects satisfying a formula in an FOL model
• represent databases to FOL models
• query databases using FOL formulas

Syntax

The language of FOL is a formal language. So, we need to provide an alphabet and a grammar. As a motivating example, let’s take our representation of “all humans are mortal”:

x(Human x Mortal x)

There are a few new kinds of symbols in this formula. The first is the quantifier , which we read simply as “all”. This quantifier is followed by the variable x, to indicate that we’re saying something about all things x. In general, variables stand for unspecified objects. They are sometimes likened to pronouns, like “he”, “she”, “it”, or the singular “they”, which stand for concrete but unspecified (by the term) objects. What follows is a formula involving that variable x, which here takes the form:

(Human x Mortal x)

There are a few other kinds of symbols worth discussing. If we want to say that Socrates is human, we use the formula

Having multiple objects be related to something is common in mathematics, where we want to talk, for example, about the product of two numbers, which we can do using infix notation and write x × y or prefix notation like ×(x, y).

In FoL, there’s also a special predicate = that allows us to say that two things are identical, such as:

We haven’t mentioned yet the other quantifier , which we read as “exists” or “there is”. So, to say that for every number there’s a bigger number, we might use the formula:

x y BiggerThan yx

The ability to have these kind of nested quantifiers is one of the strengths of FOL, and the need for them in mathematics—for example in the definition of continuity—was one of the reasons FOL was discovered.

Oh, and the usual propositional connectives , , , and are also part of FOL, of course.

So, in general, the alphabet of FOL looks something like this:

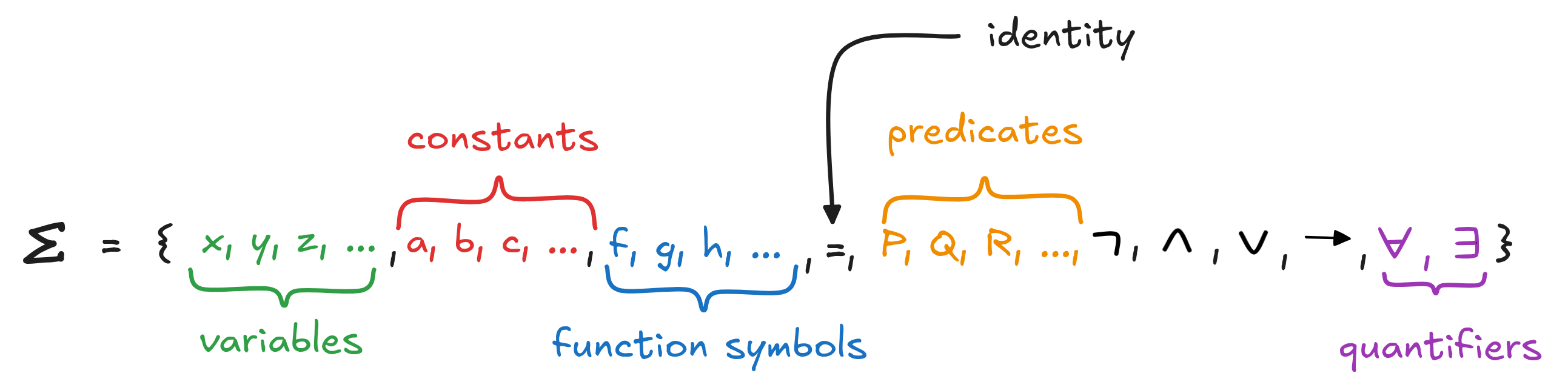
Here, we use abstract placeholders or metavariables to talk about variables, constants, function symbols, and predicates. In concrete knowledge engineering situations, however, these expressions will typically be mnemonic, like fatherOf x, distanceBetween xy, Human, BiggerThan, etc.

For the function symbols and predicates, especially when using metavariables, we need to indicate their arity, that is, how many terms can “legally” follow them. For example, fatherOf function symbol is unary, since we can write fatherOf Socrates but fatherOf x y makes no sense if x and y aren’t related. The function distanceBetween xy, instead, is binary since distance is defined between two points. Etc. Similarly, for predicates, we can write Human x, but not Human xy.

We sometimes indicate a terms arity using superscripts, like fatherOf¹, distanceBetween², Human¹, BiggerThan², etc. But often, the arity of a term is clear from the context, and then we leave it out.

Defining a grammar which generates all the formulas we’ve mentioned so-far in a precise, recursive fashion is more difficult than, for example, in the case of propositional logic.

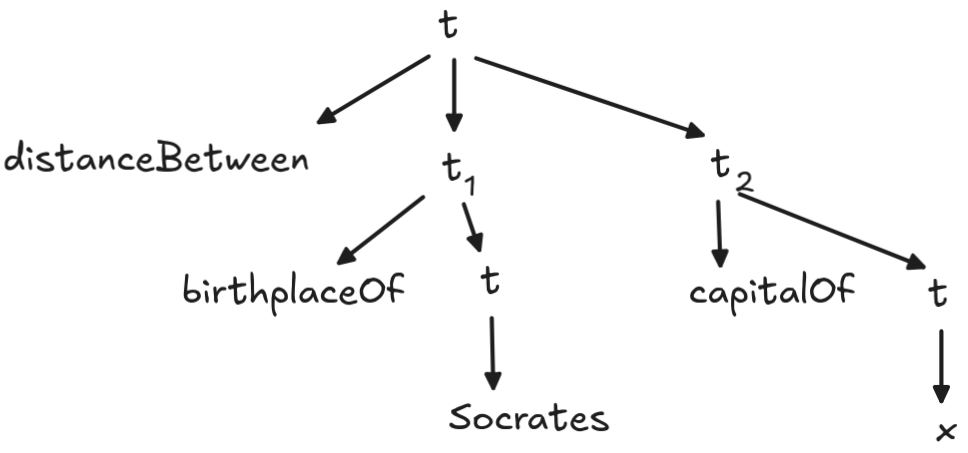
First, we need to define the notion of a term, which is a possibly complex expression for an object. Examples of terms are the variable x, the constant Socrates, but also complex expressions like

The following BNF covers all these cases:

That is, a term is a constant, a variable, or an n-ary function symbol followed by n terms. Even though our syntax doesn’t officially require parentheses in function symbol applications, we sometimes include them to increase legibility. For example, instead of

we also write something like

This grammar gives us the following rewrite rules:

• r₀: t c
• r₁: t x
• r₂: t ft₁…tₙ

Let’s apply these rules to generate the parsing tree for our term These rules generate the following parsing tree for the term:

We get:

There exists a special class of terms that will be important later, which are called ground terms. These are basically terms without variables, such as:

Their grammar, however, is easy: we just drop variables from the general grammar and obtain the BNF:

with corresponding re-write rules r₀ and r₂.

This gives us the grammar for terms, which can fill the argument places of function symbols and predicates. We use the notion of a term in the specification of the grammar for FOL formulas. In BNF, the grammar is:

A::= Pⁿt₁…tₙ ∣ t₁ = t₂ ∣ A ∣ (A A) ∣ (A A)∣ (A A) ∣ xA ∣ xA

Formulas of the form Pⁿt₁…tₙ and t₁ = t₂ are also called atomic formulas, which express basic facts like Human(Socrates), Mortal(fatherOf(x)). The grammar, then, generates the FOL formulas much like in propositional logic, just with more operations.

We obtain the following re-write rules:

• r₃: A Pⁿt₁…tₙ
• r₄: A t₁ = t₂
• r₅: A A
• r₆: A (A A)
• r₇: A (A A)
• r₈: A (A A)
• r₉: A x A
• r₁₀: A x A

We can combine these rules with the term rewriting rules to parse an entire formula and its terms at the same time. For example, for the formula,

x (Human x y (Human y motherOf x = y))

we get:

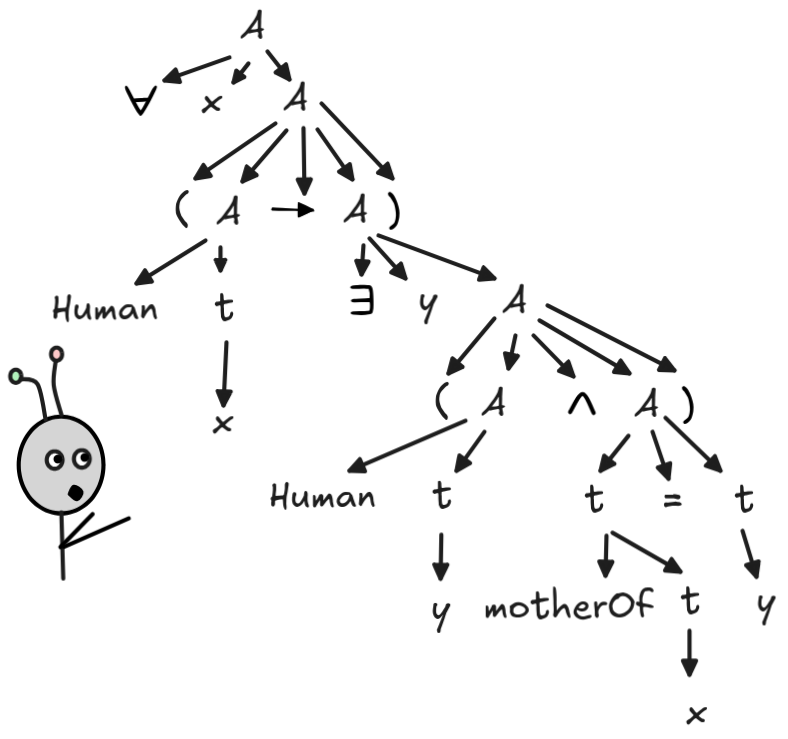
As you can see, the grammar of FOL formulas can get rather complex.

Before we move on to working with FOL formulas, we need to discuss one important syntactic issue. To illustrate the idea, consider the following formula

So far, we’ve paraphrased it as saying that x is human. But what is x? Well, we don’t know. If there would be a quantifier at the beginning of the formula, as in

x Human x

We’d be saying that there is a human or, a bit closer to the surface syntax of the formula, there exists an object such that it is human. But without the quantifier expression to “act” on the variable, the x is a term that stands for a some unspecified object.

A formula like Human(x), where some variable isn’t “captured” by any quantifier— where some variable is free—is called an open formula. In contrast, a formula like x Human x, where all variables are captured by some quantifier expression is called a closed formula or sentence. Open formulas play a crucial role in database theory, so let’s look at them a bit more closely.

It turns out that saying precisely and rigorously under which condition a variable is free and under which condition it is bound (in such a way that a computer could answer the question by parsing) is a rather subtle logical issue. We won’t go into the full details, but it’s important to be aware of the stumbling blocks.

At first glance, the way variable binding works might seem rather obvious. Take our formula from above, for example:

x (Human x y (Human y motherOf x = y))

Here it seems rather clear which variable quantifier pairs belong together. We can illustrate this, for example, in the following “wire diagram”:

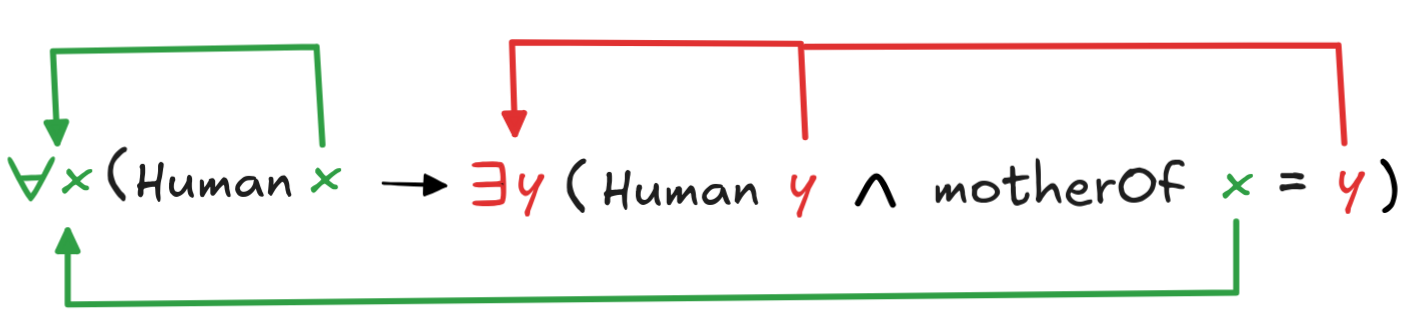
The idea is, roughly, that a variable is bound by a quantifier just in case the variable “comes after” the quantifier in the formula and the variable is the same as the one that directly follows the quantifier—we say that its the variable that the quantifier ranges over.

In logical terminology, the idea that a variable “comes after” a quantifier in a formula is expressed by saying that the variable is in the quantifier’s scope. More generally, the scope of a quantifier is the formula that directly follows it in the recursive parsing of the expression. That is, in our example, the scope of the x is the open (!) formula:

Human x y (Human y motherOf x = y)

We might be tempted to think that that’s all there is to say about binding: a variable is bound by a quantifier just in case the variable is the one the quantifier ranges over and the variable is in the quantifier’s scope. But look at the following FOL formula:

x (Human x x (Human x Mortal x))

This is a perfectly fine FOL formula. It parses and has the content that there exists a human such that all humans are mortal. But we’ve used the same variable twice in nested quantifications. While this is not illegal, it creates issues when we think about binding.

The following diagram indicates the correct bindings in the formula:

That is, even though the red x’s are in the scope of the existential x, they are not bound by it. They are bound by the later universal x, which is “closer” to them and binds them “first”. It’s possible to formulate a mathematically precise condition to exclude such cases, but for us the bottom line is that we’ve got to be careful: variables bind to the first quantifier that scopes them.

Open formulas are at the center of database theory. We can think of them as expressing properties of objects. They can be simple, like Human(x), which expresses the property of being human. Or they can be complex, like

Human x y (Human y motherOf x = y)

We can also “apply” open formulas to terms, as it were. For example, to apply the open formula

Human x y (Human y motherOf x = y)

to the term Socrates, for example, we simply replace the unbound x’s with Socrates to obtain

Human Socrates y (Human y motherOf Socrates = y)

This sentence then says that Socrates is human, as is his mother.

The operation that we’ve applied here is called substitution: we’ve substituted the free variable x with the constant Socrates. For an arbitrary formula A, free variable x, and term t, we denote this operation by writing A[x/t]. That is:

(Human x y (Human y motherOf x = y))[x/Socrates]

Human Socrates y (Human y motherOf Socrates = y)

As you’ll see, substitution plays a crucial role in FOL reasoning. The only very important caveat here is that the operation does not apply to bound variables. That is, for example:

(Human x x (Human x Mortal x))[x/Socrates]

Human Socrates x (Human x Mortal x)

Human Socrates x (Human Socrates Mortal Socrates)

Models

A model for a formal language, remember, is a representation of a possible reasoning scenario. In propositional logic, we could identify models with simple 0/1 assignments to the basic propositional formulas, the propositional variables. From this, we could determine all the other truth-values using Boolean functions. While Boolean functions still play a role in the semantics for FOL, the simple approach no longer works here.

When we consider a formula like x (Human x Mortal x), we’re saying something about all things. To determine whether such a statement is true in a given reasoning scenario, we need to know which things exist in the scenario. This is determined by providing what’s called a domain of discourse or simply domain for our language.

A domain is simply put just a (non-empty) set of objects. So, it could be, for example:

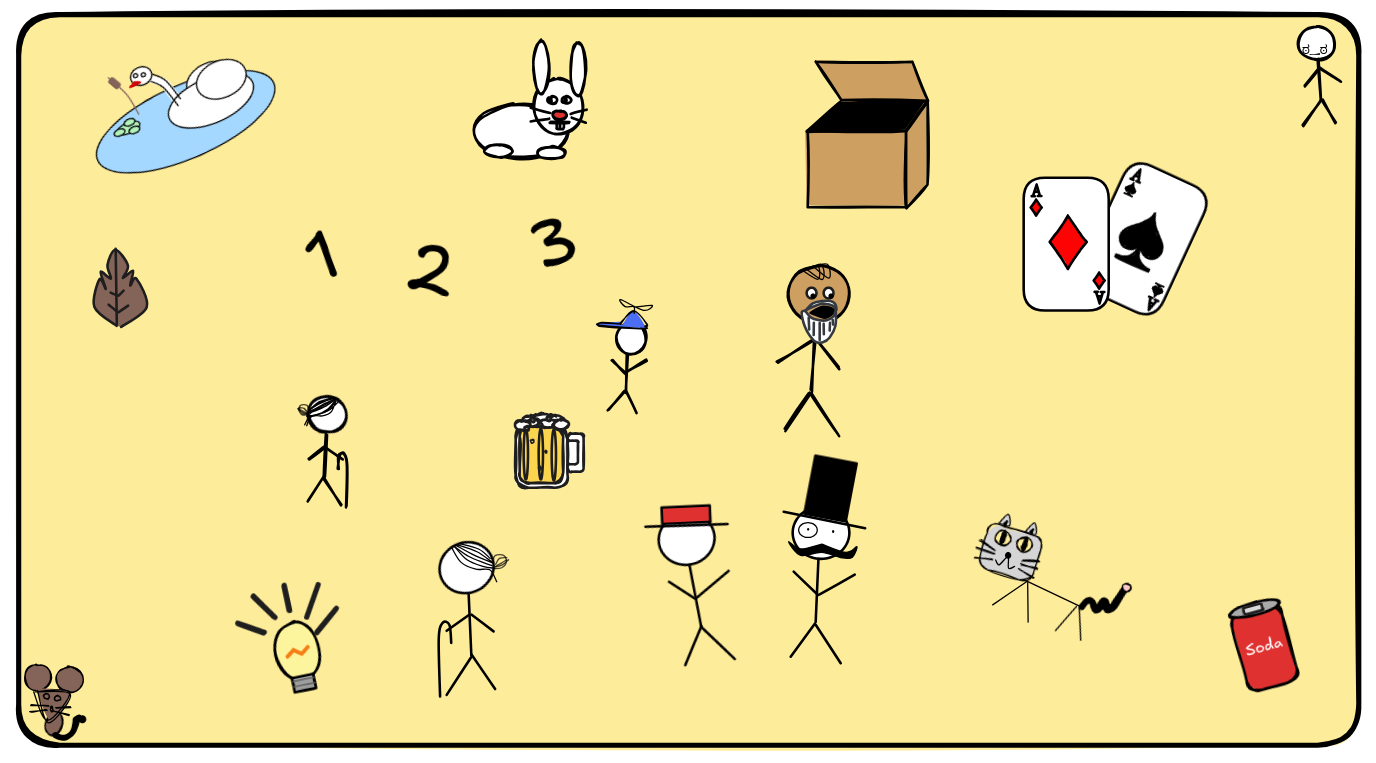
This domain is very populated, it contains many of our old friends: little Jimmy, Mr Sir, and Granny Smith, but also the numbers 1,2,3 and the Mighty Box from when IA  tried magic in chapter 2. And many other things. Specifying a domain is the first step towards providing a model for FOL. We typically denote the domain of a model by D.

But simply knowing what’s in the domain is not enough to determine the truth-values of our formula. We also need to know what the constants, function symbols, and predicates of our language express over this domain. We indicate the interpretation of a term over a model using so-called semantic brackets  and  . That is a is the interpretation of the constant a, also called its denotation, f is the interpretation of the function symbol f, and R is the interpretation of the predicate symbol R, also called its extension.

Let’s look at the constants first. These are expressions like Socrates and Xanthippe, or, depending on our language, names like littleJimmy and MrSir. The idea is that constants are proper names, that is, they denote objects. So, Socrates is simply going to be a member of the domain, the thing that is called Socrates in that model. So in the model that corresponds to reality, we would have, for example:

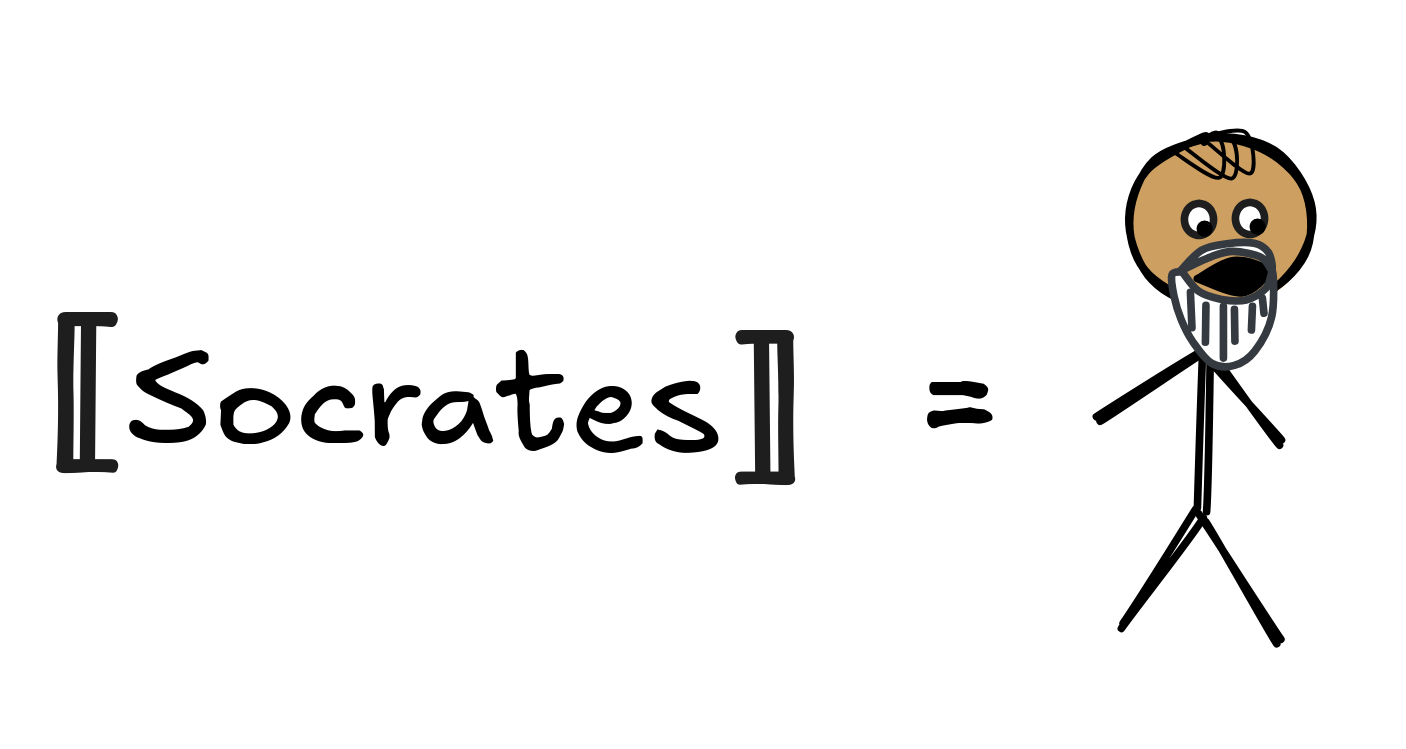
But there are, of course, reasoning scenarios where Socrates denotes little Jimmy:

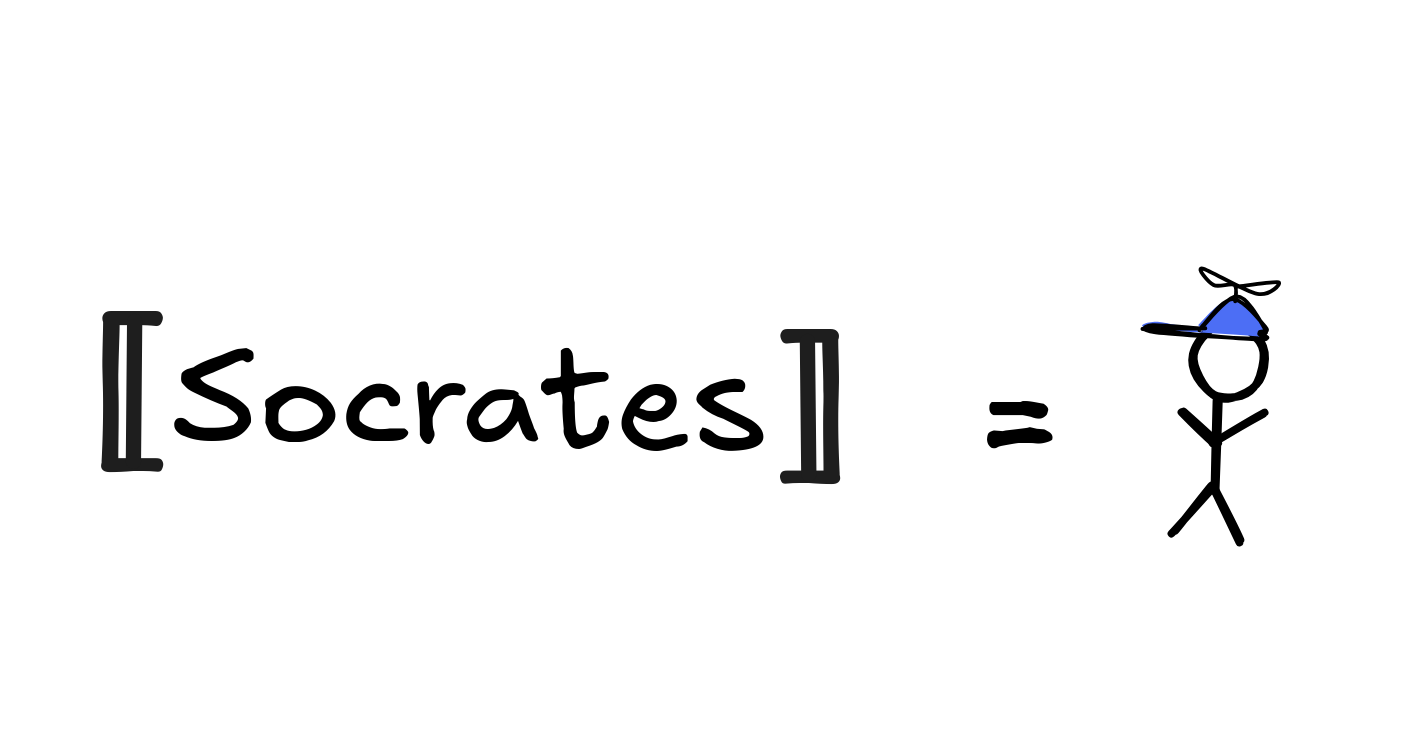
We might even call the light bulb Socrates:

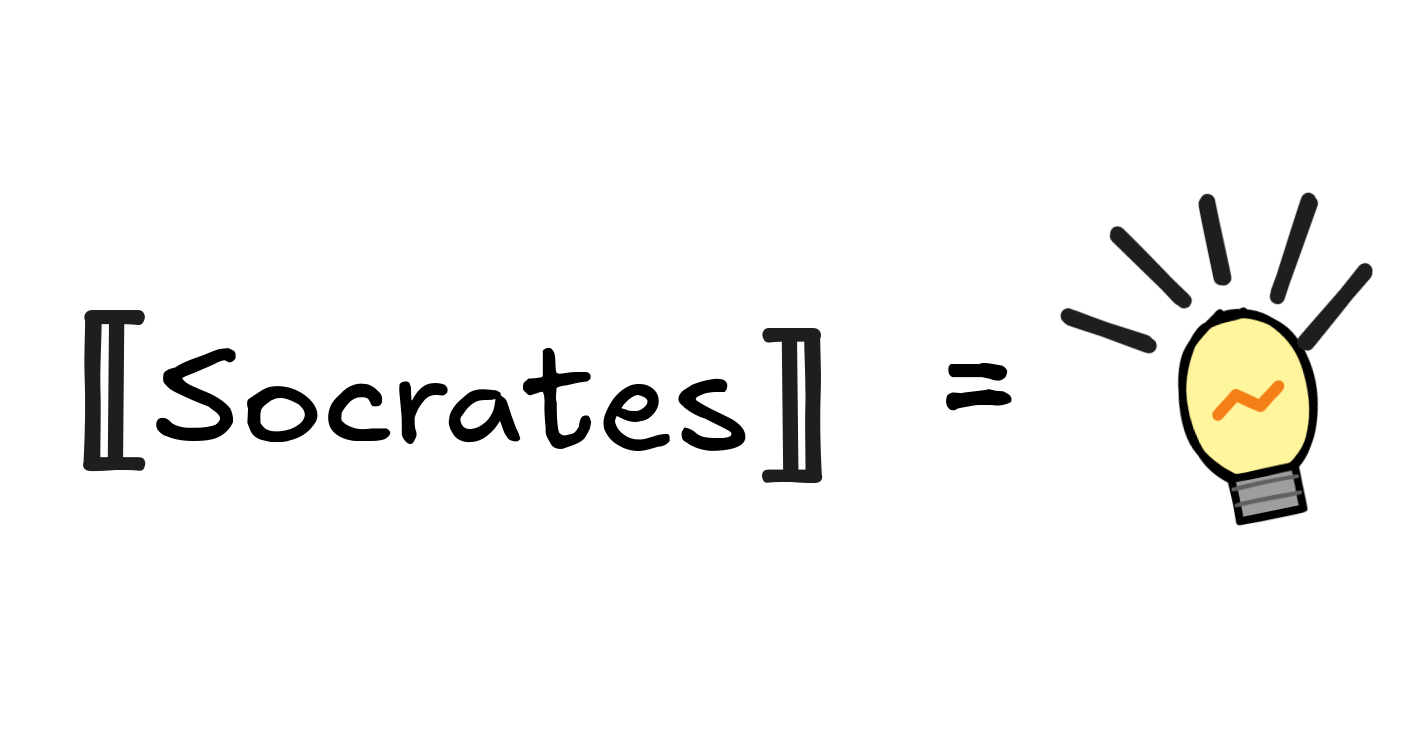
Next, there are function symbols, like fatherOf, birthplaceOf, distanceBetween, etc. While the idea for how to interpret them is straightforward, they also present some difficulties. Function symbols stand for functions, so we interpret them as such: as mathematical functions which are defined on the domain.

The easiest way of specifying such an interpretation is by means of a function table, like we used for the truth-functions in Boolean algebra. In the case of a unary function symbol, like fatherOf, we could have:

That is, we say that Mr Sir is the father of both little Jimmy and Linus, Mad Man is the father of Mr Sir, Socrates is the father of Granny Smith, and so on.

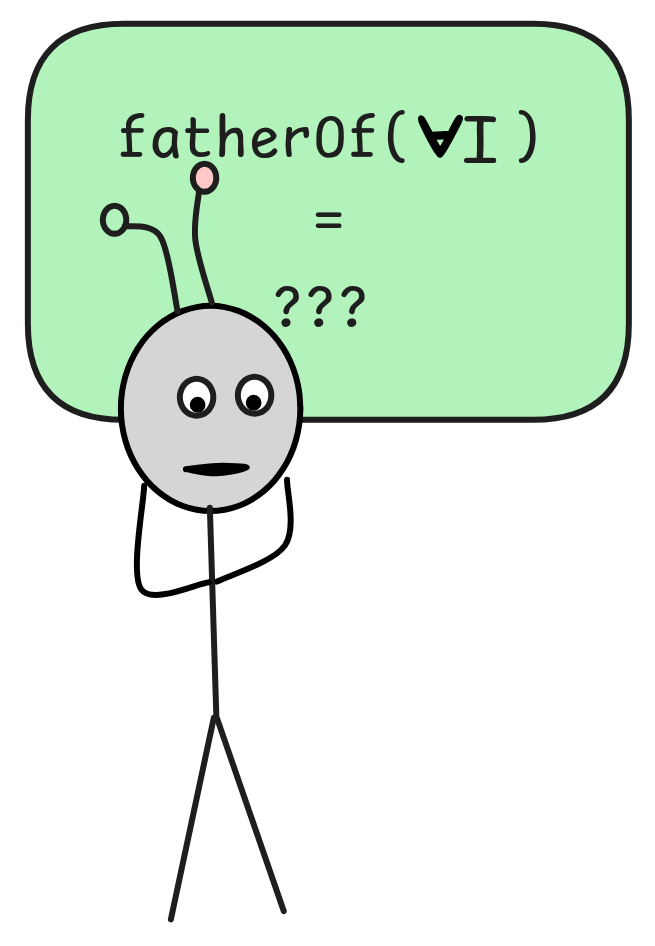But now the issues begin. In classical FOL, the function symbols need to denote total functions, that is, functions which give an output for every input. This creates some obvious problems with fatherOf. Which value should we assign to the light bulb, to the Mighty Box, or to the number one? In fact, if our domain only contains finitely many things there will be a family “loop”, where someone is their own grandⁿ-father.

We could use partial functions—functions that are sometimes undefined—to solve the issue, but that would mean we’d move out of the realm of classical logic. If the father of Socrates would be undefined, which truth-value should we assign to the claim that his father is human? Neither 0 nor 1 are good options, so we seem to want to say that it’s undefined as well. But handling undefined truth-values requires different techniques, so we’ll postpone that to later.

For now, we basically treat these resulting oddities as a side-effect of our modeling: they are simplifying assumptions, which we know not to be adequate, but which we can handle if we are aware of them. For example, we use a function symbol like fatherOf only in a language that talks exclusively about humans, perhaps we introduce an idealized first human who’s their own father, and so on.

In fact, these kind of issues persist on various levels. For example, the following is, from a logical perspective, a perfectly valid interpretation of the distanceBetween function symbol:

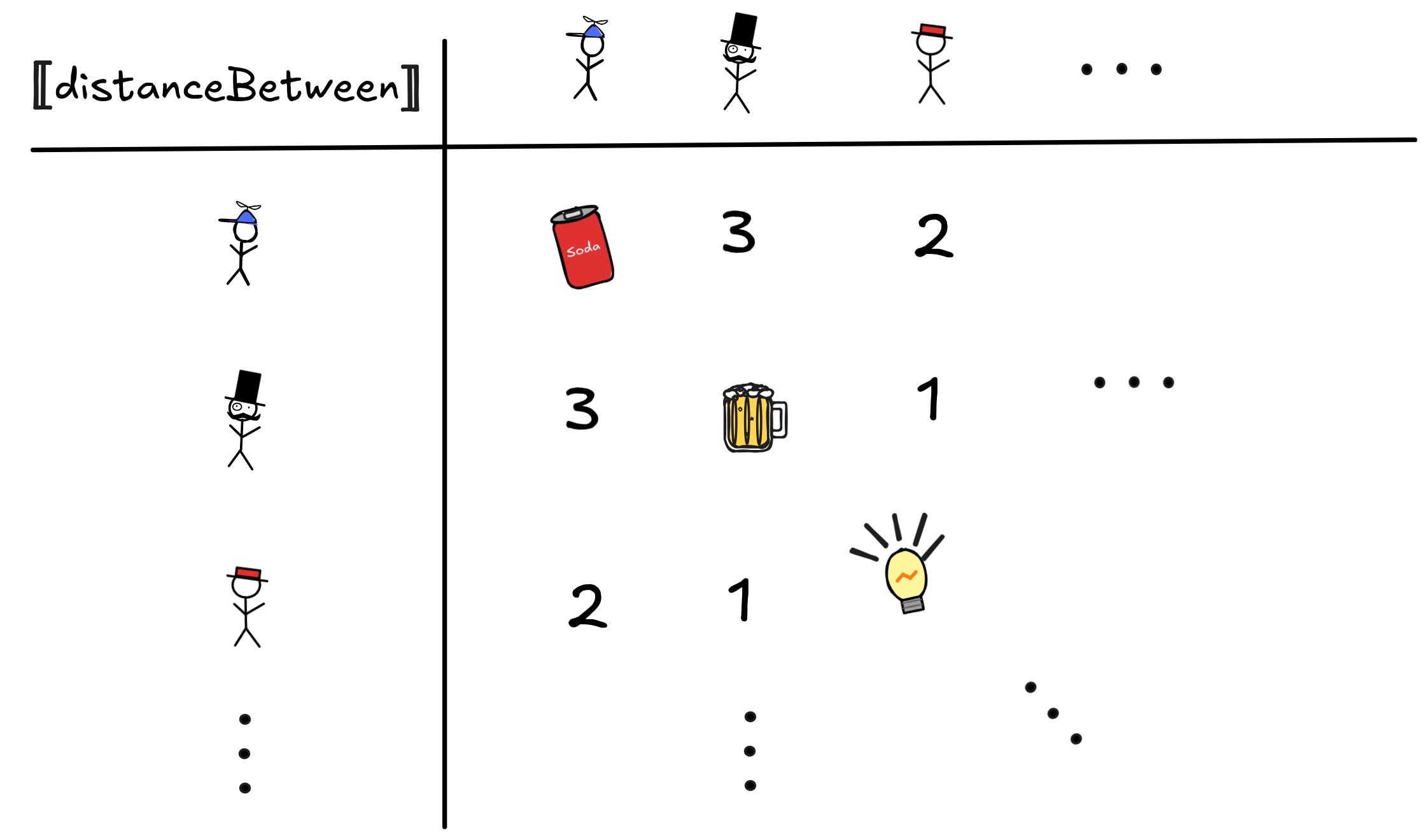
Any object in the domain is a valid output for the function. What it means to say that the distance between little Jimmy and himself is a soda I don’t know— but it can happen in an FOL model. You need to be aware of such issues when you’re knowledge engineering with FOL.

One thing that will be important is that once we’ve interpreted the constants and function symbols, we can recursively calculate the denotation of all—possibly complex— ground terms . Take the term

distanceBetween(birthplaceOf (Socrates), capitalOf(Greece))

distanceBetween ( birthplaceOf ( Socrates ), capitalOf ( Greece ))

f t₁…tₙ = f ( t₁ , …, tₙ )

This leaves only the predicates uninterpreted. We begin with unary predicates—that is, predicates with one place, like Human and Mortal from our formula x (Human x Mortal x). The idea is that we the interpretation in a model is simply the set of objects from the domain, which, according to the model, have the property expressed by the predicate. Here’s an example of what such an interpretation could work out:

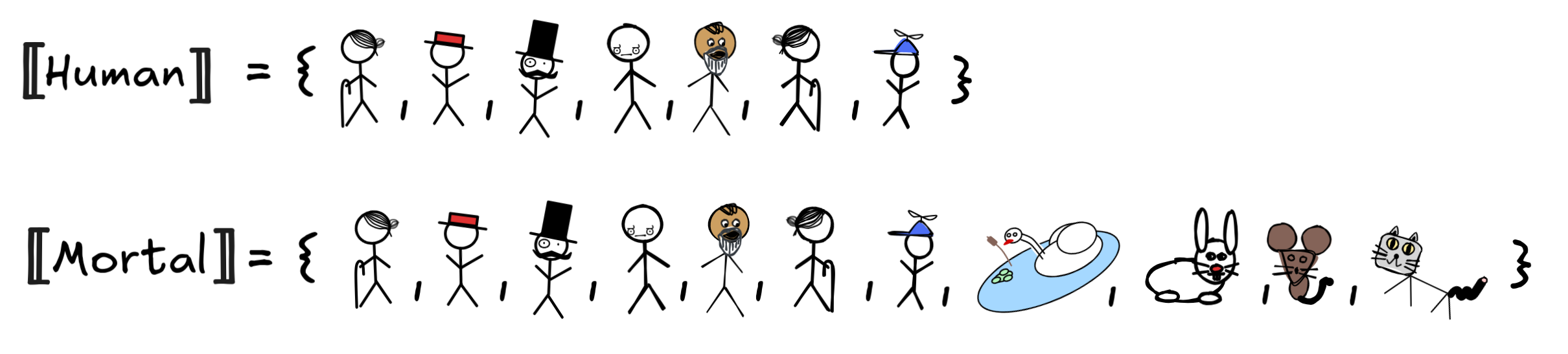
This is, in a sense, the most natural interpretation of the predicates: Human applies to all the things that we normally think of as humans, and Mortal to all the things we normally take to be mortal. Humans and animals are mortal, boxes, numbers, and beers are not. As you can probably tell already, in this model x (Human x Mortal x) will turn out to be true.

It’s important to remark, though, that other interpretations are possible. We’re modeling possible reasoning situations—hypotheticals. So, we could have a model where, for example, little Jimmy, Mr Sir, and IE  aren’t mortal, but the rabbit and lamp are human:

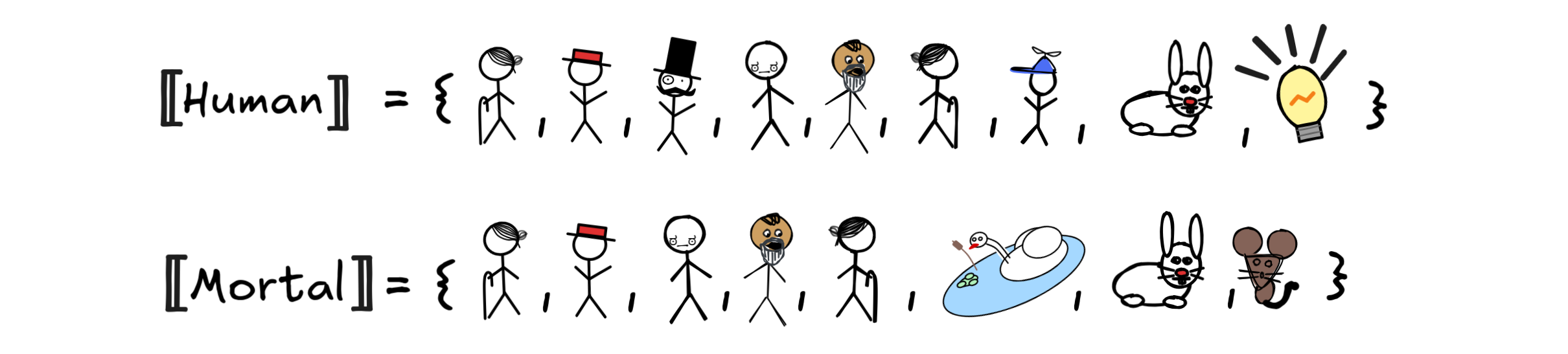
This is a perfectly valid FOL model. And as you can probably tell already, in this model x (Human x Mortal x) will turn out to be false since little Jimmy is human but immortal.

To generalize this idea to predicates with more than one place, like the binary BiggerThan or the ternary LiesBetween. In order to interpret them, we use tuples of objects in the domain. A tuple is essentially an ordered [list]( https://en.wikipedia.org/wiki/List_(abstract_data_type) of objects of finite length. Here are a few examples of tuples over our domain with their respective lengths using Python-style list notation:

Note that with lists, order and multiplicity matters: although both lists have length 2, the list with Granny Smith in first and Linus in second place is different from the list with Linus in first and Granny Smith in second place. And the list with the Ace of Spades in place 1 and 3 still has length 3.

The idea is that we can interpret predicates in general as sets of lists: the lists of objects that satisfy the predicate. So, for example, the interpretation of BiggerThan, will be the set of lists of length 2 such that the first element of any list is bigger than the second thing in the list. Here’s an example of how this could work over our domain:

This would mean that Linus is bigger than little Jimmy, Mr Sir is bigger than Linus and little Jimmy, little Jimmy is bigger than the Mighty Box, and so on. As in the unary case, the interpretation of BiggerThan can be natural as in the example, or “weird” as in the following:

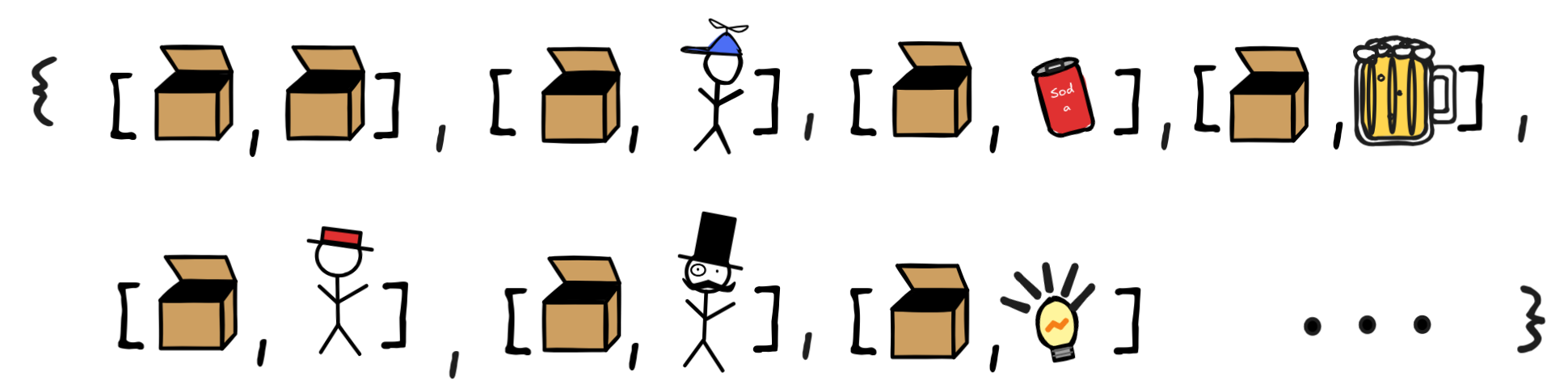
Here the Mighty Box is bigger than everything—including itself.

Note that, in contrast to function symbols, the interpretations of predicates don’t need to be total: not everything needs to be related to everything. For example, if we have the binary predicate Sibling to say that two things are siblings, the following is a perfectly fine interpretation:

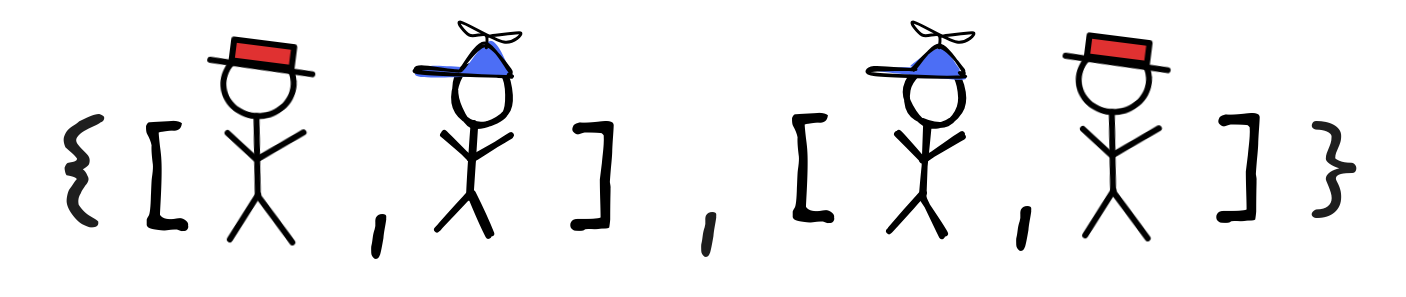
That is, it’s fine to say that Linus and little Jimmy are each other’s siblings and no one else in the domain is thusly related. Note that this doesn’t create undefined values, as any pair that’s not in the set is simply not related, which means 0 and not undefined.

This idea, then, generalizes to ternary predicates like LiesBetween, where [LiesBetween] will be a set of lists of length 3, where the first item in every list lies between the second and the third item.

In fact, the idea generalizes to all predicates. We can say, in general, that the interpretation of an n-ary predicate—a predicate with n places—is a set of lists of length n. Note that this even works in the case of unary predicates, like Human and Mortal. We can just think of sets of objects equivalently as sets of lists of length 1. That is, we don’t really need to distinguish:

There are two ways of representing the interpretations of the predicates that are very common in computer science and AI contexts. First, if we’re dealing with unary and binary predicates only, we can straightforwardly represent the interpretation of using graphs. Here’s how this works:

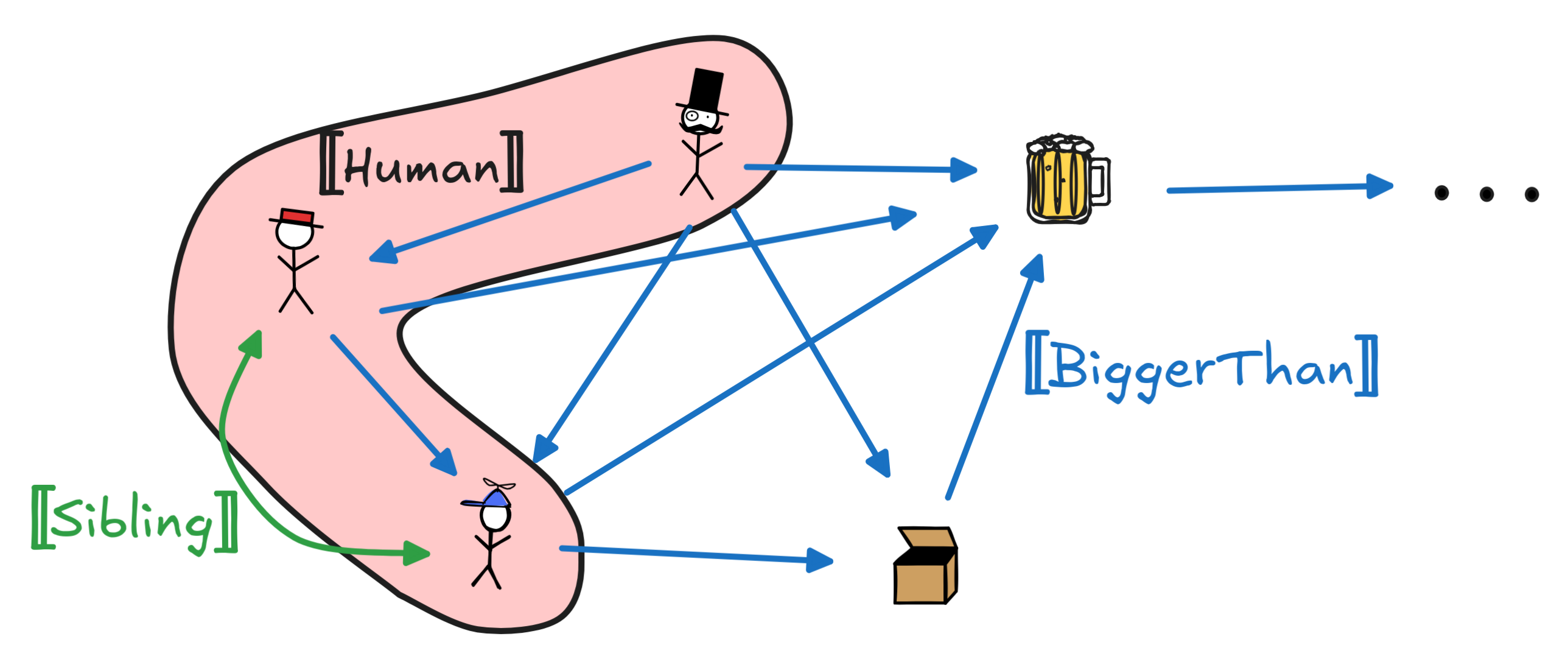
What’s going on here is that we interpretations of unary predicates are represented as sets and we’re using arrows to indicate that a relation holds between two objects with the arrow pointing from the first relatum to the second.

This way of representing models makes them special cases of so-called knowledge graphs, which are an important technology that’s been used by search engines like Google and others to structure data.

The other way of representing the information in a model is crucial for database theory. The idea is that we can alternatively write a set of lists as a table. Here’s how this plays out with our interpretations for Human, BiggerThan, and Sibling from before:

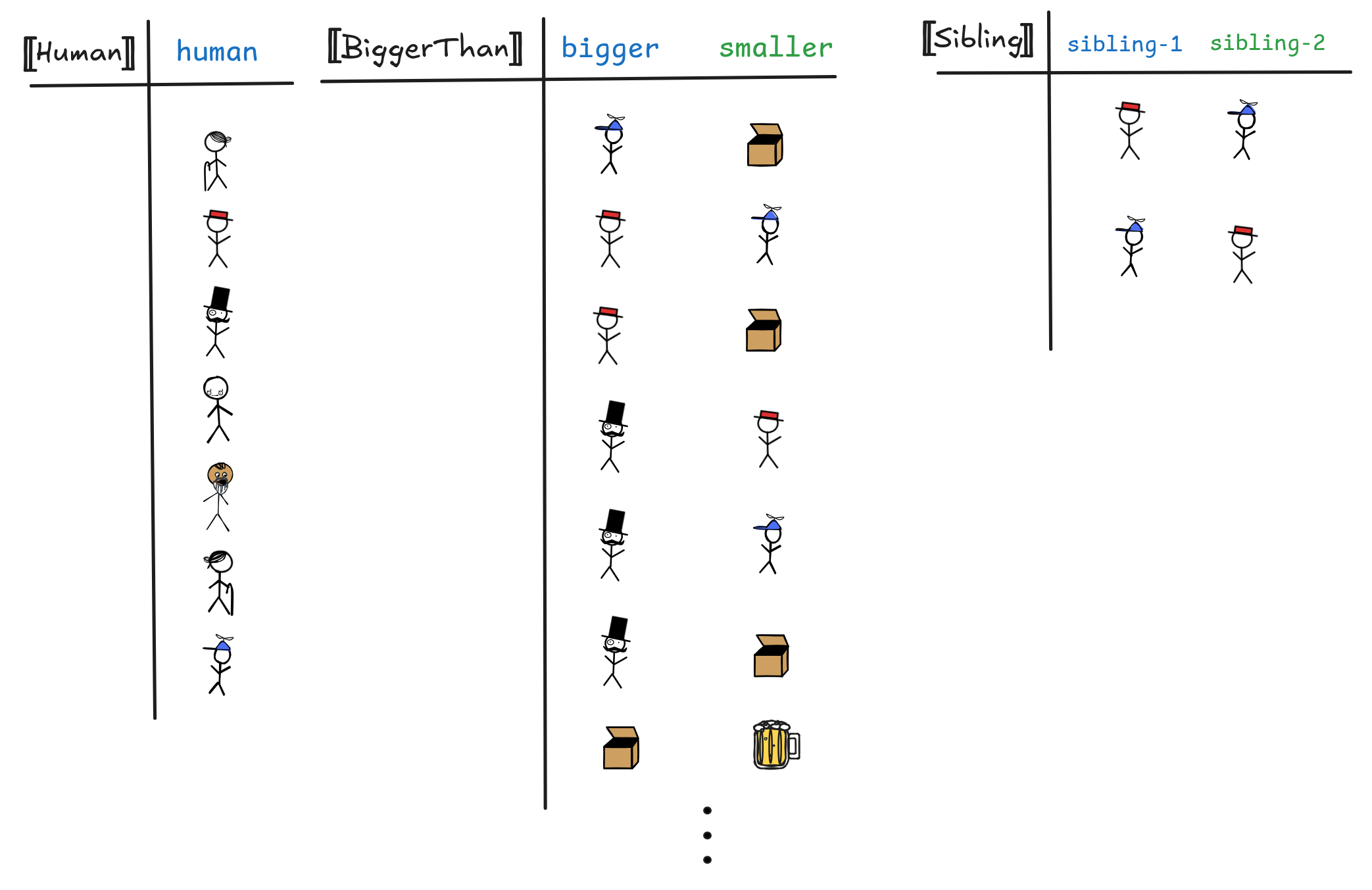
In these tables, each row corresponds to a list and in this way represents a basic relational fact. The first table is basically just a list of humans. The second table gives us the interpretation of BiggerThan with the bigger thing occupying the first column and the smaller object the second, as suggested by their headers. The bigger and smaller in the header go by different names: “attributes”, “identifiers”, … but what’s important here is that this naming is “internal” to the table and not officially part of the interpretation. It just clarifies what the table does.

This gives us the basic ingredients for an FOL model:

• a (non-empty) domain D,

• a denotation a D for each constant a,

• a mathmetical function f for each function symbol f, which maps inputs from the domain to outputs from the domain,

• an extension R for each predicate symbol.

When we’re dealing with different models, we often name them, like M and N or M₁ and M₂ etc., and we superscript the domains and interpretations by that name. So Dᴹ is the domain of model M and Dᴺ the domain of model N, Socrates ᴹ is the denotation of Socrates in model M and Socrates ᴺ is the denotation of Socrates in model N, and so on.

Truth and Satisfaction

It’s time to turn to truth. The information provided by an FOL model is enough to calculate the truth-values for all the formulas in its language. Let’s figure out how.

In FOL, we typically write

M A

to say that the formula A is true according to the model M. If we want to directly talk about the truth-value of a formula, we denote it by A . Since we’re working in classical logic, we’ll assume that A { 0, 1}. The two notations are related by the following equivalence:

M A   if and only if   A = 1

Our aim right now is to define M A for all formulas A.

The simplest case are the so-called ground formulas, which are atomic formulas—a predicate applied to terms—without any variables in them. Take the ground formula Human LittleJimmy, for example. The natural thought is that this sentence ought to be true in a model just in case the denotation of LittleJimmy is in the extension of Human in that model. This gives us the first basic truth-condition:

M Human LittleJimmy   if and only if   LittleJimmy Human

This idea generalizes quite straightforwardly to binary predicates and ground expressions involving complex ground terms. For the formula

M BiggerThan Socrates fatherOf LittleJimmy

[ Socrates , fatherOf ( LittleJimmy )] BiggerThan

As a general formula, we get:

M P t₁…tₙ   if and only if   [ t₁ , … , tₙ ] P

The case of identity claims with ground terms is equally straight-forward. Take, for example, the formula:

M Socrates = fatherOf LittleJimmy

Socrates = fatherOf ( LittleJimmy )

Note that the = in the formula and the = in the condition are different uses of =: the first is a formal symbol, which we interpret using the “real” identity relation =.

Once we’ve calculated the truth-values of the basic formulas, we can calculate the truth-values of their truth-functional combinations—formulas constructed using , , , —in the familiar recursive fashion we know from Boolean logic:

M A	if and only if	NOT A = 1
M (A B )	if and only if	A AND B = 1
M (A B )	if and only if	A OR B = 1
M (A B )	if and only if	((NOT A ) OR B ) = 1

In fact, by some simple Boolean reasoning, we can directly give a recursive definition of M A as follows:

M A	if and only if	M A
M (A B )	if and only if	M A and M B
M (A B )	if and only if	M A or M B
M (A B )	if and only if	M A or M B

In this sense, what we’re doing in FOL is an extension of the framework of Boolean algebra.

The main question is how to interpret quantifiers and . But before we can do that, we need to talk about variables the x, y, z, …. Logical theory knows different ways of handling the variables of FOL. There are approaches that take them to be denoting terms, which requires the use of so-called variable assignments. These work in a similar way as variable assignments in programming language, where you can set the values of x, y, z to something like so:

x = socrates
Y = little_jimmy
z = mr_sir

And then, later, you can set the values to something else:

x = little_jimmy
Y = little_jimmy
z = little_jimmy

Working with assignments has a series of advantages from a logical perspective. Most importantly, it allows us to assign truth-values to open formulas like

(Human x Mortal x)

Here’s how this works. We’ve already mentioned the idea that an open formula like (Human x Mortal x) expresses a property—in this case the complex property of being human and mortal. Another way of putting the idea is to say that open formulas express conditions that objects can satisfy: any object in our domain either is or isn’t a mortal human.

A natural idea, therefore, is that the semantic value (Human x Mortal x) of the open formula (Human x Mortal x) is not a truth-value but a set of objects: those objects that satisfy in the model the condition expressed by it. Let’s work this idea out in some more detail.

Suppose we have some object d D, which lives in our domain. To check whether the object satisfies (Human x Mortal x) what we can do is to add a new constant d to our language with the stipulation that:

d = 1

That is, we give the object an ad hoc name, which makes it possible for us to talk about d in our formulas. Then, we can say that d satisfies the open formula (Human x Mortal x) just in case replacing x with the new term for d gives us a true formula, that is:

M (Human x Mortal x)[x/d]

The crucial point here is that if we replace the x with d, we obtain a ground formula—here (Human d Mortal d)— whose truth we can determine using the methods we’re already familiar with.

In practice, we sometimes use the object itself as a constant that denotes itself. So, we write things like:

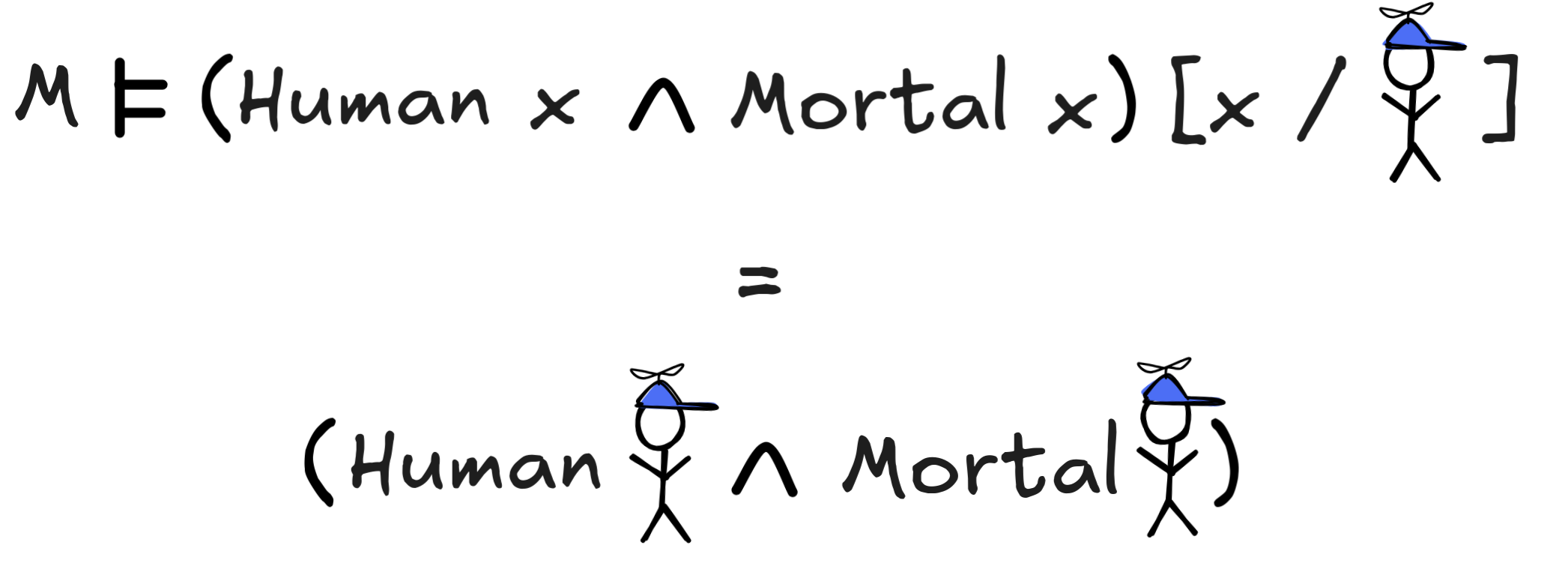
The truth-conditions then work out to:

That is, in our normal model, where all humans are mortal, little Jimmy satisfies the open formula, in the model with immortal Jimmy, he doesn’t.

It’s worth remarking that this approach, though common in AI practice, is on shaky logical footing and requires a lot of technical care to be worked out rigorously—it can be done, but we won’t go into the logical details. When it comes to DB’s, however, we’ll see a non-shaky version of it.

The idea of satisfaction allows us also to define the very useful notion of the extension of an open formula: the set of objects satisfying a predicate. In the case of (Human x Mortal x), for example, this works out to:

(Human x Mortal x) = { d D | M (Human x Mortal x)[x / d] }

More generally, if A(x) is any open formula with exactly one free variable, we can define:

A(x) = { d D | M A[x / d] }

This approach can also be generalized to open formulas with more than one free variable. Take the following formula, for example:

BiggerThan x y Human x

This formula is not satisfied by a single object, but by a list of objects from the domain [d, e] satisfies the formula just in case

M (BiggerThan x y Human x)[x /d, y /e]

M (BiggerThan d e Human d)

where we give ad hoc names to both d and e and substitute them in for x and y in our free formula. This gives us the notion of an extension for this formula as well:

(BiggerThan x y Human x)

{ [d, e] | M (BiggerThan x y Human x)[x / d, y / e]}

A crucial observation that we’ll refer back to later is that just like the interpretations of predicates, we can represent the extensions of open formulas as tables. The extension of open formulas with one variable is just a table with one column, like this table, which gives the extension of Human x Mortal x in the model with immortal Jimmy:

Note that little Jimmy is immortal in this model and thus not in the extension of the predicate.

And for binary predicates, we get tables with multiple columns. Here’s (part of) the table for (BiggerThan x y Human x) in the model we’ve described earlier:

What’s going on here is that we’ve eliminated all the rows where the first column had a non-human in it, like Mighty Box.

This notion of satisfaction of an open formula by objects in a model is a core notion in database theory and is what ultimately underpins database queries.

But before we go into this, we need to talk about the truth-conditions for quantifiers. But the notion of satisfaction makes quick work of this. Let’s take again our formula:

x (Human x Mortal x)

(Human x Mortal x)

M x (Human x Mortal x)   if and only if   (Human x Mortal x) = D

This idea generalizes rather nicely. If A is a formula with precisely one free variable, we can also write A(x) to indicate this. We can then write our clause as follows:

M x A(x)   if and only if   A(x) = { d D | M (A(x))[x/d] } = D

This works exactly analogously for the existential quantifier  . Take the formula

x (Human x Mortal x)

(Human x Mortal x)

(Human x Mortal x)

M x (Human x Mortal x)

(Human x Mortal x) ≠ { }

x A(x)

M x A(x)   if and only if   A(x) ≠ { }

For the recursive evaluation of formulas, it’s helpful to slightly rewrite the resulting clauses. To see how this works, think about under which conditions we have that A(x) = D, and under which A(x) ≠ { }. For concreteness sake, let’s take the formula Mortal x as A(x). For Mortal x = D, what needs to be the case is that for all objects d D, we have that M Mortal d, that is, we have to have:

M Mortal and M Mortal and …

Mortal x ≠ { }

d D

M Mortal d

M Mortal or M Mortal or …

This gives us two very clearly recursive clauses for the truth of quantified sentences:

M x A	if and only if	for some d D, M A[x/d]
M x A	if and only if	for every d D, M A[x/d]

This gives us the concepts of a model and truth in a model for FOL. We are now in a position to investigate how valid inference in FOL works. But given its unique combination of practical importance—in math, science, and AI—with technical … trickiness, we dedicate an entire chapter to this. What we’ll look at now is a connection of FOL models to AI research that is on a much lower level: the relation to databases—the way we store knowledge and any kind of data in complex computer systems.

Databases and FOL

Roughly speaking a database (DB) is an organized collection of data. Data can be essentially be any sequence of symbols, but we’ll look at data that is a bit more structured. Our running example will involve information about the capitals of different countries, in which part of the world they are located, which language are spoken there.

We’ll store this data as plain text in a SQL database, which is by far the most widely used database system. If you’ve ever heard of someone professionally using a database, chances are it was some form of a SQL database. SQL is a domain-specific programming language, which in contrast to general purpose programming languages, is used for one specific purpose: to interact with data.

In SQL, data is stored in tables. Before we can put data in those tables, we need to CREATE them. Here’s some SQL code that sets up three tables, one for storing information about the capitals of countries, one for storing information about where those countries are located, and one for the language spoken in the country:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

CREATE TABLE CapitalOf (
  country TEXT PRIMARY KEY,
  capital TEXT NOT NULL
);

CREATE TABLE LocatedIn (
  country TEXT PRIMARY KEY,
  continent TEXT NOT NULL
);

CREATE TABLE Language (
  country TEXT,
  language TEXT
);

Don’t worry, you don’t need to install anything. In the moment, there will be a link that allows you to interactively execute the code in the browser.

In any case, running this code doesn’t do much, it just sets up the three tables. Next, we need to populate them, we need to INSERT data INTO the tables. Here’s how that goes:

15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

INSERT INTO CapitalOf VALUES
  ('United States', 'Washington D.C.'),
  ('Netherlands',   'Amsterdam'),
  ('Germany',       'Berlin'),
  ('Italy',         'Rome'),
  ('Japan',         'Tokyo');

INSERT INTO LocatedIn VALUES
  ('United States', 'North America'),
  ('Netherlands',   'Europe'),
  ('Germany',       'Europe'),
  ('Italy',         'Europe'),
  ('Japan',         'Asia');

INSERT INTO LanguageOf VALUES
  ('United States', 'English'),
  ('Netherlands', 'Dutch'),
  ('Germany', 'German'),
  ('Italy', 'Italian'),
  ('Japan', 'Japanese');

Running this code also doesn’t return anything (other than some success message), it just populates our tables with data. This data is now ready to be interacted with: we can store it, update it, or query it, which is to ask the DB for information.

Here’s a very simple QUERY, which returns all the data in our table:

1
2
3
4

SELECT * FROM CapitalOf;
SELECT * FROM LocatedIn;
SELECT * FROM LanguageOf;

To run this code click RUN after following this link.

The output looks something like this:

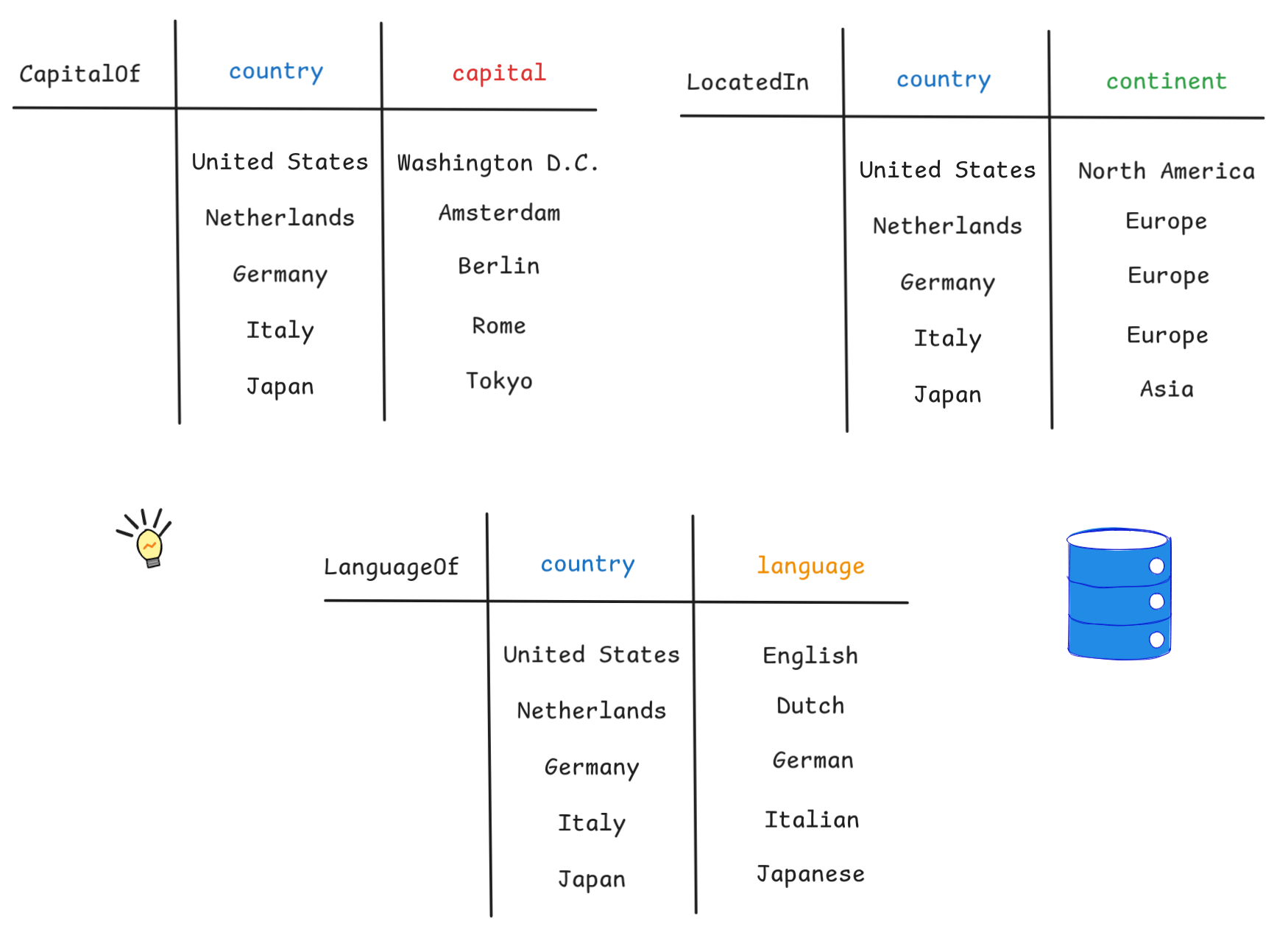
But wait a second, that looks suspiciously like the specification of an FOL model using tables! In fact, it is a model for language with three binary predicates:

It turns out that this is not by chance. On the low level, there is a very deep correspondence between FOL syntax and models and the way SQL databases work. In fact, SQL was originally developed on the basis of relational algebra, which Codd’s theorem proves to be “essentially equivalent” to FOL. This result is analogous to the relationship between logical proofs and computer programs, which we’ve observed in the Curry Howard Correspondence and which is the basis for proof assistants like Lean. In an analogous way, FOL is the basis for DB theory. Let’s explore this idea a bit further by looking at a more complicated query:

1
2
3
4

SELECT country
FROM LocatedIn
WHERE continent = 'Europe';

If you copy-paste this code into the Query field of our db-fiddle, you’ll get a table like this:

But hang on, the similarities continue. Suppose that our language had constants for the countries (UnitedStates, Netherlands, Germany, Italy,Japan), continents (NorthAmerica, Europe, Asia), and languages (English, Dutch, German, Italian, and Japanese), with the stipulation that these constants indeed denote the corresponding countries, this table gives the extension of the open formula:

We can carry this idea much further:

1
2
3
4

SELECT CapitalOf.capital
FROM CapitalOf
JOIN LocatedIn ON CapitalOf.country = LocatedIn.country
WHERE LocatedIn.continent = 'Europe';

This returns:

But this is just the extension of

y (CapitalOf(x,y) LocatedIn(y,Europe))

If we systematically explore these observations, we find that there is a direct correspondence between SQL queries and open FOL formulas: this is a core idea of Codd’s theorem. This correspondence carries on to a very low level: the algorithms SQL implementations use to return data for queries are algorithms for FOL model checking. Much more could be said about this, but that’s the content of a course on DB theory. What the take home message is for today is that the way we store knowledge in computer systems and query that knowledge is intimately related to FOL, making it one of the core logical methods for AI.