By: Rick Nouwen and Johannes Korbmacher

Formal languages

When we try to develop AI systems, we immediately run into an issue: computers, which are the basis for any modern AI technology, “speak” a different language than us—the proverbial 1’s and 0’s.

That is, even if we understand what intelligent behavior is and we manage to break it down into instructions that a computer can, in principle, follow, we still need to express these instructions in an unambiguous language that the computer can “understand” (i.e. execute). We need to write code.

Moreover, since intelligent behavior involves knowledge about the world and acting on the basis of such knowledge, we need to be able to communicate such knowledge to any prospective AI system. That is, we need a way to represent our knowledge about the world.

The solution to the first problem are—of course—programming languages, which are precisely defined, rule-based systems for expressing unambiguous instructions in a language that we can understand, but which we can automatically transform into instructions that a computer can understand. The solution to the second problem are knowledge representation languages, which are systems of precisely defined expressions that can represent various facts about the world.

It turns out that, fundamentally, both programming languages and knowledge representation languages are instances of the same kind of mathematical structure: they are formal languages.

Formal languages have their origin in the study of valid inference—in logical theory—but today they are one of the most widely used logical tools in AI and other disciplines that employ logical tools.

In this chapter, we’ll study formal languages, how they are defined mathematically, and how they are used in logical theory and AI.

At the end of this chapter, you’ll be able to:

explain the ambiguity and over-expressiveness of natural language using examples
define formal languages using formal grammars
parse logical formulas using rewrite rules and parsing trees
represent simple facts about the world using the language of propositional logic
name standard examples of formal languages and their use cases

Formal vs. natural languages

English, St̓át̓imcets and Ripuarian are examples of natural languages. Python, propositional logic and algebraic chess notation are examples of formal languages. What makes a language a natural language and what makes it a formal one?

We all speak at least one natural language and many of us speak multiple. A natural language is a naturally evolved system that you learn spontaneously, for instance by interacting with your parents and other people around you when you are very young. Native speakers of English, St̓át̓imcets or Ripuarian didn’t learn their native language at school or by studying grammar books, but simply by being in an environment where the language was used. Because natural languages are acquired in this way, they are also very susceptible to change. They constantly evolve, just by being used and passed on to next generations.

In contrast, nobody learns Python, propositional logic or algebraic chess notation simply by interacting with their parents. Also, these languages clearly didn’t evolve naturally and while the conventions of these languages may change over time, they do not do so spontaneously, but rather because a community of users explicitly decides to make a certain change.

Having command of a natural language is an extremely powerful skill. It allows you to communicate with others about your desires, your thoughts, your observations, your plans. It allows you to learn things in school, to teach other people what you have learned, to enjoy art in the form of literature, poetry and song lyrics, to laugh at jokes, to persuade others to change their actions, etc. etc.

Most of the recent advances in AI make use of the fact that natural language is such a pervasive part of our lives. Because language is everywhere, it creates an enormous wealth of data about many facets of human existence and human cognition, ready as input for machine learning. Given this, why don’t we just use natural language for everything in AI? What do we need formal languages for?

There are many different reasons formal languages are important in general and for AI in particular. One reason that is relatively quick to appreciate is that powerful large language models trained on natural language are developed using programming languages, which are formal languages. We cannot construct a neural network using natural language. So even sub-symbolic approaches to AI rely on formalisms that have symbolic roots.

More generally, however, natural languages have some properties that make them unsuitable for doing logic or maths and, equally importantly, that make them unsuitable for storing human knowledge. Two such properties stand out:

Natural languages are ambiguous: Statements formulated in a natural language can often be interpreted in multiple ways. As a consequence, if we choose to use natural language as a basis for drawing inferences, we can’t always be sure that rules or facts that we want would want an AI system to benefit from are understood in the appropriate way.
Natural languages are over-expressive: Specific statements made in a natural language tend to describe highly specific thoughts. This makes natural language unsuitable for studying generalities in valid inference.

Let us discuss both these properties in more detail.

Ambiguity

Imagine that we want to build an AI system that gives out safety advice on eating foraged mushrooms. We have access to a lot of expert knowledge about mushrooms. One idea could be to feed this knowledge to the AI system in the form of natural language statements. For instance, we could give the system lots of English language sentences that together make up all our knowledge. Say, these sentences include the following:

S = If a mushroom has red spots and gills, then it's not poisonous.

Also, we prompt the AI system with another English language sentence:

T = The mushroom in front of me has red spots and gills.

It may seem straightforward how the AI system can prepare an advice on the basis of the knowledge captured in S and the information in the user prompt T .

We may think that all the AI system needs to do is recognise that it can apply the deductive inference pattern known as modus ponens (MP), which licenses the inference from an if-then statement together with the if-part to the then-part: from “if the door is open, you can come in” and “the door is open”, you can infer “you can come in.” Schematically, modus ponens licenses all the inferences of the following form, where A and A are any two statements: 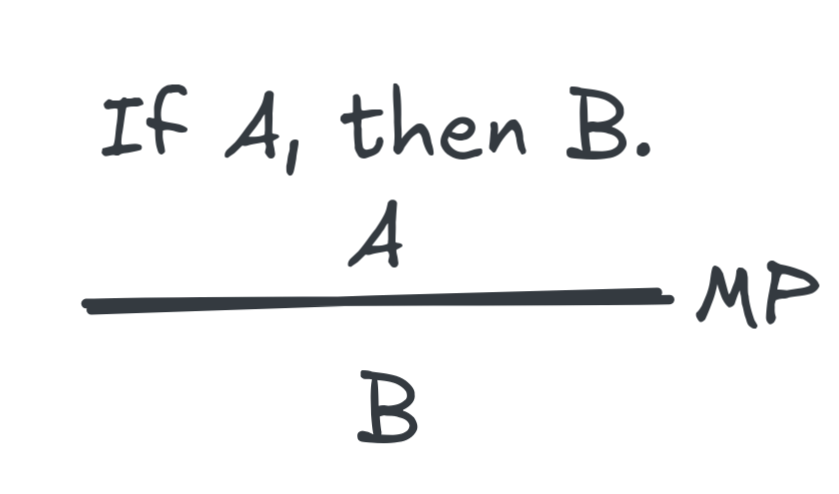Applying this principle, then, you would expect that from the two statements above the AI system should infer that the mushroom in question is not poisonous.

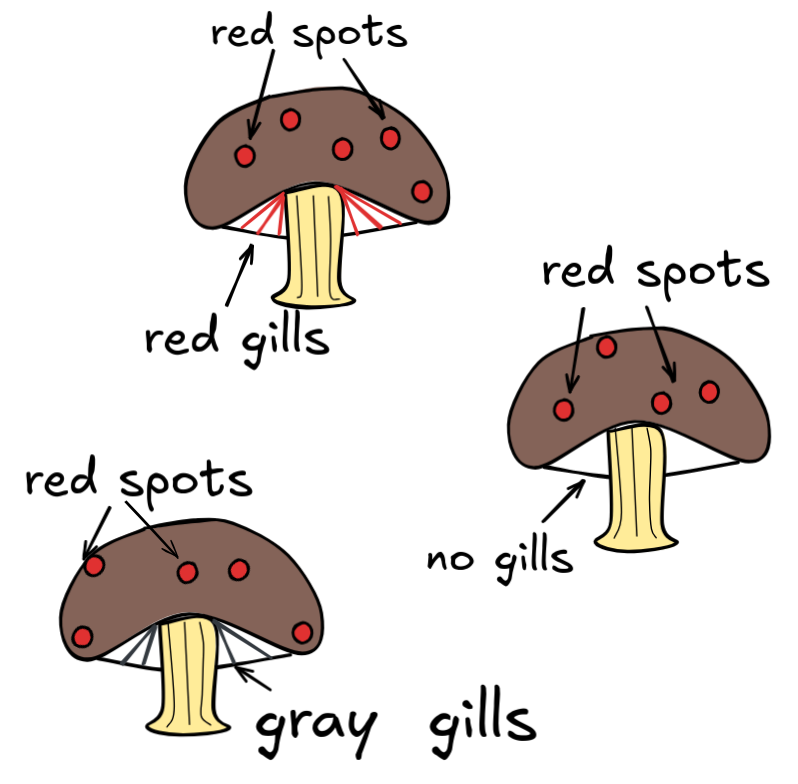
The problem, however, is that “the mushroom in front of me has red spots and gills” is ambiguous. It could either mean that the mushroom has red spots and red gills, or it could state that it has red spots and that it has gills (of whatever colour). Because of this we cannot be sure what either of these statements are saying exactly. It is not clear what the rule is that S is intended to capture, nor is it clear what observation the user is describing with T . And because of all that uncertainty, we cannot be sure whether modus ponens applies. For instance, perhaps S is intended to mean that mushrooms that have red spots and red gills are not poisonous, while T is intended to mean that the mushroom in question has gills (gray ones, in fact) and red spots. In that case, modus ponens would not apply. In other words, if our AI system accidentally interprets these sentences not as they were intended, it could end up applying modus ponens and cause the users to poison themselves.

A similar problem concerns the words “if” and “then” in languages like English. Say, I remove the ambiguity in S above and instead state that:

S' = If a mushroom has red spots and red gills, then it's not poisonous.

It is now clear what this means. It tells us what is the case when a mushroom has the features that are mentioned. Does this tell us anything about mushrooms that do not have red spots and red gills? For most people, the intuition is that it does not: on the basis of just S' I cannot conclude anything about a mushroom with black gills and no spots.

The problem, however, is that “if” and “then” are not always understood in this way. Imagine yourself saying this to a child:

U = If you behave well, I will buy you an ice-cream.

This clearly tells the child, via modus ponens, what happens when they are well-behaved. However, in this case the statement also seems to be saying what happens when they do not behave well. U seems to clearly suggest that if the child does not behave well, then there won’t be any ice-cream.

So, “if” and “then” are interpreted differently in different examples. This simple observation has profound consequences for AI. If we feed the AI system our knowledge in the form of a long list of English sentences of the form

If A, then B

how does the AI system decide which of these to interpret the way we interpreted S' and which to interpret parallel to our understanding of U ? The use of a natural language complicates the storing of knowledge, since a single natural language sentence often come with more than one interpretation.

Ambiguity is extremely common. Whenever we want represent knowledge and rules precisely, we should avoid the inherent ambiguity of natural language. Formal languages allow us to do just that. Let us now turn to a second reason why we choose formal over natural languages.

Over-expressiveness

To illustrate the problem of over-expressiveness, let us look at another case of modus ponens:

Say a magician places a rabbit in a cardboard box and they close the box. After a short while they open it again and show the audience that the box is empty. The audience gasps. Why? Because on the basis of a common assumption like M and modus ponens, the audience expects the box to contain the rabbit. An object was placed in what looks like a normal box, we didn’t see anything happening to the box, so we infer via modus ponens that the object is still in the box.

Members of the audience now need to somehow reconcile the empty box with what they saw. They have a number of options. It looked like the box was a normal box, but perhaps it wasn’t. Perhaps there is some trick that lets the rabbit escape from the box unseen by the audience. In that case, this is not a normal box and modus ponens would not allow us to conclude that the rabbit is still in the box. Similarly, the audience didn’t see anything happen to the box, but perhaps the magician managed to distract his audience and perhaps he removed the rabbit in a way we couldn’t see?

Once more, modus ponens does not apply and we do not end up inferring that the rabbit is in the box. Another possibility is that the rabbit is still in the box. That is, we were right to apply modus ponens, but we are wrong in our observation that the rabbit is gone. (Perhaps the magician isn’t showing us all of the box?) Finally, and most interestingly, perhaps some people in the audience take this failure of modus ponens as evidence that M must be false. In other words, these people believe in magic.

Now, compare this story to the following statement:

Say now I calculate:

a x b = c

and both a and b are odd. I observe that c is an even number, then there’s a few options again. Perhaps I was wrong to believe that a x b = c , or perhaps I was wrong to believe that a and b are both odd. Or perhaps my observation that c is even was wrong. An arrogant person may even believe that their maths book is wrong in stating N .

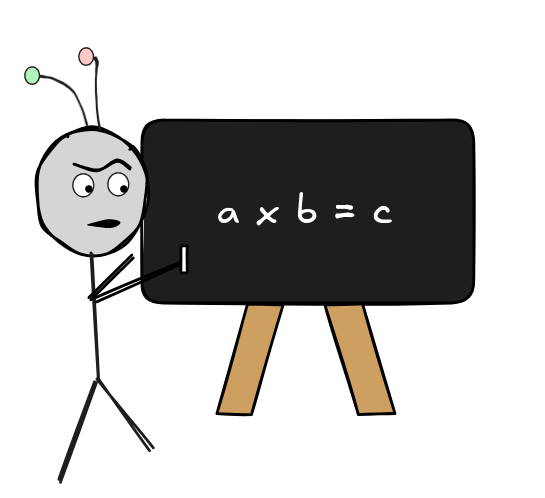In any case, both the case of magic and the case of odd number multiplication show that modus ponens is a very strong inference. As soon as we have all the ingredients for modus ponens, we cannot help but draw the conclusion. And if that conclusion is not in line with what we observe, we start questioning our assumptions and our observation.

The two stories also show that modus ponens is a very general inference. It exists completely independent of subject matter. Structurally, the story above about M is completely parallel to that of N .

This is where the over-expressiveness of natural language comes in. We can use natural language to express individual cases where modus ponens applies, as we just did above. But because natural language is so good at talking about the specific details of situations, it can make us lose sight of the more general, abstract patterns that underlie our reasoning—it is very bad at abstracting away form logically irrelevant details. M and N are highly specific examples of premises that with the right further premise bring us in a situation where we can apply modus ponens. To be able to talk about modus ponens as a general principle of valid inference, we would need to let go of the specifics in these examples and state the principle using an abstract formal language. This can be very hard to do in natural language.

From a logical perspective, however, both stories have the same underlying structure. In both cases, we have a conditional statement—an “if-then”-statement—of the form

If A, then B.

In the first example, M , we have:

A = We put an object in a cardboard box and nothing happens to that box

B = The object will remain in the box

In the second example, N , we have:

A = We multiply two odd numbers

B = The result is odd

In both cases above, we thought If A, then B was the case, as was A . But in both cases, we also thought B was not the case. Given that this clashes with modus ponens we start questioning our assumptions. Either something is wrong with our assumptions A or If A, then B , or something’s wrong with our belief that B .—Logic allows us to do make such reasoning very explicit and very general. By using a formal language we can focus on the pattern underlying our mechanisms of valid inference.

In other words, when we study valid inference, we often do not care about the specific content of the statements our inferences are built on. It would be extremely hard to define a notion like modus ponens using just a natural language. The abstraction offered by a formal language makes it possible to make explicit what all inferences that are to be classified as such have in common.

More generally, when we study systems of valid inference, we are often looking to find out what the consequences are of our assumptions about logical laws. If we only had natural language to study this, which sentences should we use then? Should these be about mushrooms, rabbits, numbers, or ice creams? Similar considerations apply to mathematics. Highly abstract formal languages allow us to focus on the important things. We all learn that we can simplify a quadratic equations like

x² + 5x + 6 = 0

(x+3)(x+2)=0

by factorization, which means that x is either -3 or -2 . Just imagine doing this without the use of abstract symbols like x !

Formal languages

Formal languages are neither ambiguous nor over-expressive. They were specifically designed as mathematical models of language, which abstract away from irrelevant details in a formally precise fashion. This is precisely what makes them so great for “talking” with computers: they solve the issue of precision that we mentioned at the outset. In fact, it turns out that they are also able to represent knowledge about the world, but we’ll return to this point later.

So far, you’ve only had a glimpse of what a formal language looks like. We have not specified one formally yet. Before we can go ahead and give the mathematical definition of what a formal language is, we need to talk a bit more about sets. Formal languages are sets. So, we need to know what a set is before we can talk about formal languages.

Sets

A set is the simplest kind of collection of objects. All that matters to a set is which things are in it and which things are not. If some object x is in a set, we say that x is one of its elements or members. Elements of a set are also said to belong to the set or to be contained in the set. Beyond membership, nothing matters to a set. For instance, there is no order to the elements in a set and an object is either in the set or not - it cannot be in a set multiple times.

It can sometimes be helpful (but also sometimes hurtful!) to think of a set as “bag” of objects from an ambient “space”. Consider the following illustration:

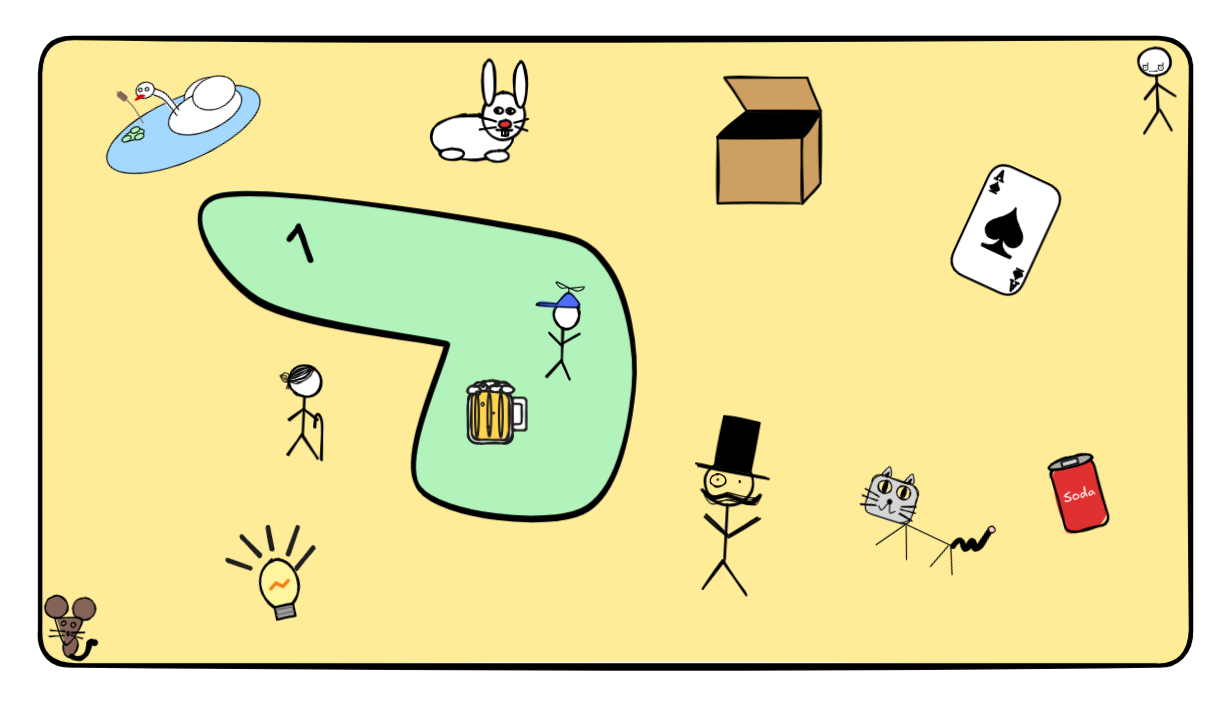
The yellow rectangle is out ambient space of objects, everything in its confines is a potential member of our set. It contains a bunch of things: animals, people, drinks, playing cards, numbers, …. The green area is a set in this space: the set that contains little Jimmy, my beer, and the number 1. It’s important to keep in mind, though, that this is just a visualization aid. Sets really are mathematical objects, not areas in space. There are sets that are impossible to draw or locate.

A set may contain any kind of object: numbers, symbols, people, or even other sets. For S a set and s an object, we write a ϵ S to say that a is an element of S , and we write a ϵ/ S to say that a is not an element of S . If we have many objects a₁, ..., aₙ , then we also write a₁, ..., aₙ ϵ S to say that a₁ ϵ S and a₂ ϵ S and …, and aₙ ϵ S .

If the elements of a set are precisely a₁, ..., aₙ , then we can denote the set by

{a₁, ..., aₙ}

This is called an extensional definition of the set. So, for example, the set 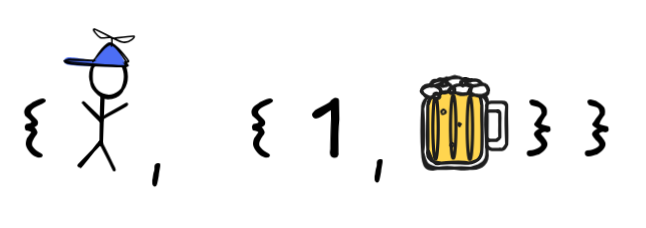contains precisely little Jimmy and the set that contains the number 1 and my beer as elements. That is, the set has two elements, not three. This also shows why we can’t “draw” all sets: how do you manage to draw a set that contains a set in a space?¹

For most interesting sets, however, we cannot give an extensional definition. One reason for this could be that we may not know exactly what the elements are. For instance, if the elements of a set are precisely the objects satisfying condition Φ , then we can denote the set by:

{x : Φ(x)}

This is called a definition by set abstraction. For example, if I have the quadratic equation

x²+5x+6 = 0,

then we can express the set of solutions to this equation as:

{x : x²+5x+6 = 0}.

In other words, we have a way of expressing the solutions, even if we do not yet know what they are. By the way, it turns out that this abstracted set is equal to the extensional set

{-3,-2}.

Another reason why non-extensional definitions are handy is because many of the kinds of sets we want to study are typically infinite. For example,

{x : x is a prime number}

is the set that contains all and only the prime numbers. So we have, for example:

3 ϵ {x : x is a prime number}

but

4 ϵ/ {x : x is a prime number}

But by Euclids theorem, there are infinitely many prime numbers. So, for reasons of time and space, we could never write down a list of all the prime numbers for an extensional definition of the set.²

Most formal languages that we will encounter will be infinite sets. So what exactly is a formal language? Put simply, a formal language is a set of sequences of symbols. Symbols are the building blocks of a formal language. A formal language starts with the specification of what these building blocks are. We call this an alphabet, which is just a set of symbols. Using the alphabet, we then use a grammar to construct the set of sequences, i.e. the formal language.

Alphabets

Sequences of symbols are recruited from an alphabet. We usually write Σ to denote the alphabet of a language.

It’s important to note that the alphabet can be any set. So, e.g.,

Σ={0,1,2,3,4,5,6,7,8,9}

is a perfectly fine alphabet. You can use it to define the language of all the numerals (terms for natural numbers).

One way to do that is to use an operation called the Kleene star, named after the American mathematician Stephen Kleene and written as an asterix. The set Σ* is the set of all sequences that you can build with the elements of Σ . This set is a formal language and it includes sequences such as 15935304888 , 249583 , and simply 2 . This is not the set of what we normally consider to be numerals, though, since Σ* will also include sequences like 000000001 and 000881 , which are not numerals (in the Western Arabic decimal system, at least).

So, while the Kleene star gives us a way to construct the set of all sequences made from an alphabet, most formal languages we are interested in will be a specific smaller subset of Σ* . This is why we need a grammar.

Grammar

The grammar of a language determines which sequences of symbols from Σ are valid expressions of the language.

In the case of most formal languages in logic, grammars use a technique known as inductive definition. Here is an example of such a definition for the set of all numerals built from Σ .

The following are all numerals: 1,2,3,4,5,6,7,8,9
If N is a numeral, then so are N0 , N1 , N2 , N3 , N4 , N5 , N6 , N7 , N8 , N9 .
Nothing else is a numeral.

Here’s how this definition works: In the first step we get all the numerals that can be written as a single digit. This is the whole alphabet with the exception of 0 . , which isn’t a numeral. Then in the second step we can represent numbers that correspond to sequences of any length >1 . For instance, this definition shows that 120 is a numeral:

1 is a numeral (step 1);
12 is a numeral (step 2);
120 is a numeral (step 2).

Using this inductive definition, there is no way to show that 01 is a natural number. Given the final line of the definition, we must conclude that it is therefore not a numeral.³

The language of logic

Just like the language of numeral notation we saw above, logics are also sets of sequences of symbols. We often refer to these sequences as formulas, so a logic is a formal language consisting of formulas. In order to specify such a language, we will want to specify an alphabet and a grammar so that the formulas that make up the formal language are well-formed sequences that are useful for the study of valid inference. Here, we will define the language used for propositional logic.

Starting with the alphabet, we should first note that, in logic, not all elements of the alphabet play the same role. (Similarly, in the case of the language of numbers we saw that 0 played a different role than the other digits). For propositional logic, the alphabet consists of three kinds of things:

propositional variables: symbols that stand for propositions
operators: symbols that operate on or connect propositions
auxiliaries: symbols that indicate how parts of a formula combine

An example of an alphabet for the language of propositional logic is:

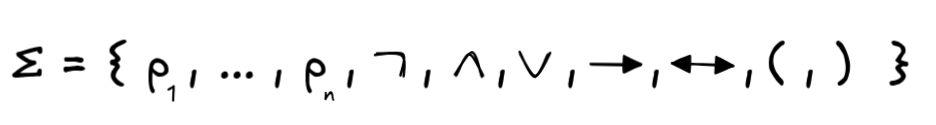
Here, p₁, …, pₙ are the (propositional) variables, 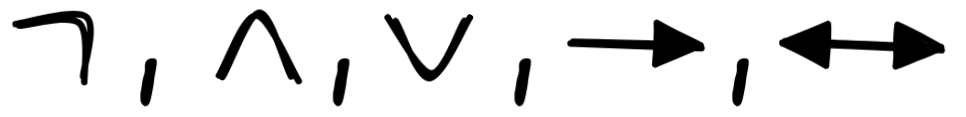are are the operators, and ( and ) are the auxiliaries.

The operators have the following conventional names and readings:

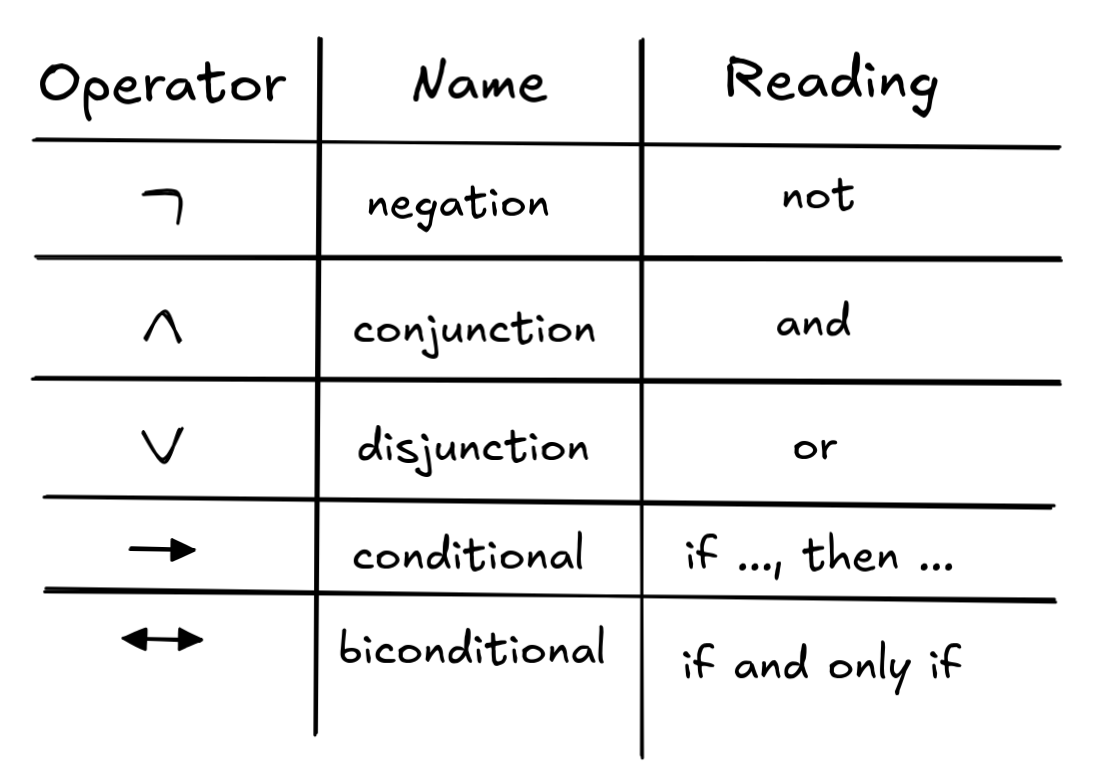
The Kleene star of this set, Σ* , provides us with all the sequences that we can build using these symbols. Σ* , contains meaningful expressions like:

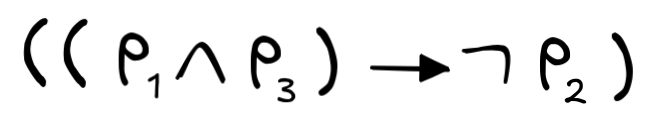
but also lots of expressions that are not well-formed for propositional logic, like:

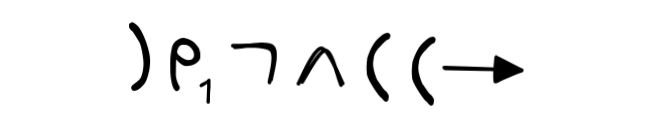
So, we should give an inductive definition for the language of propositional logic, which we will call L :

p₁, ..., pₙ ϵ L and
if A ϵ L , then 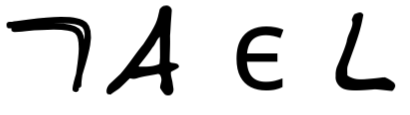, as well as
if A, B ϵ L , then .

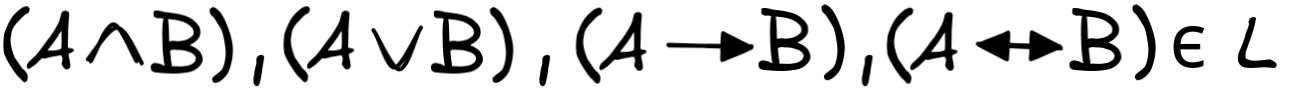As before, crucially, we assume in addition that nothing else is in L , but from now on, we will leave this “closure condition” implicit. In other words, we assume that if something complies with the above statements, then it is indeed in L , but if it does not, then it is not.

We can now easily see that 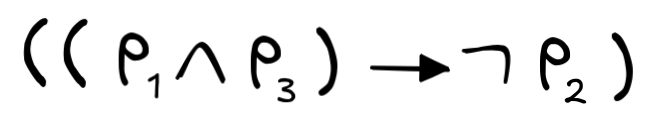is a member of L . To see this, we simply perform the construction:

We know that p₁ and p₃ are formulas (by the first clause of the inductive definition).
So, we know that 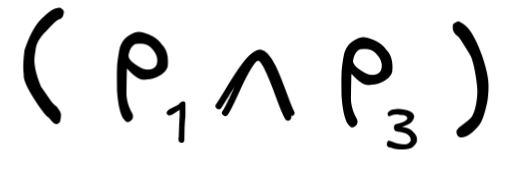is a formula (by the third clause and 1.).
We know that p₂ is a formula (by the first clause).
So, we know that 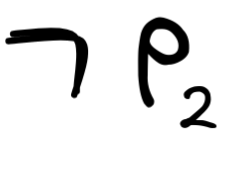(by the second clause and 3.)
So, we know that 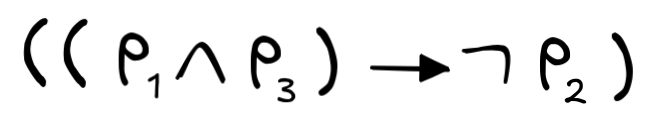(by the third clause and 4. and 5.)

But we can also see that is not a formula, since no rule every allows for to occur in a formula without being followed by formula.

In computer science and AI, there is a wide-spread notation that significantly simplifies the above rules: the so-called Backus-Naur Form (BNF). In BNF, instead of all of the above, we can simply write the following to define the same language L :

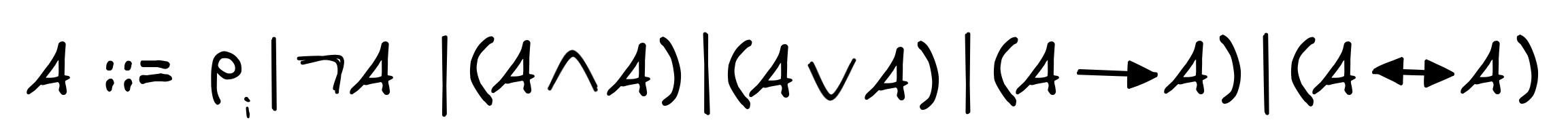
Here, we read the | as an “or”. And so this reads: a formula is either a propositional variable, or the negation of a formula, or the conjunction of two formulas, or ….

You should know that BNFs sometimes take different forms. Here is an equivalent way of giving the BNF for the same language:

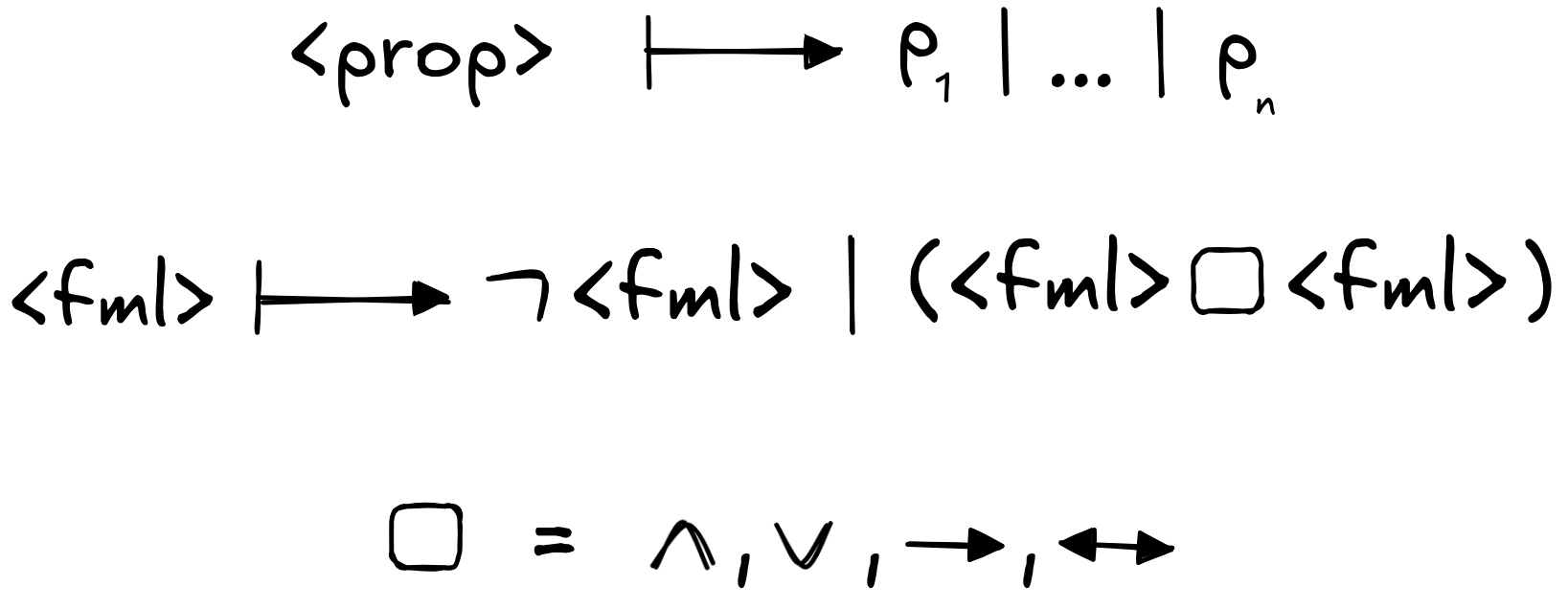
but these are just notational differences.

BNFs are a powerful method for defining formal languages. They are frequently used in logic, computer science, and AI. At this point, you know enough about how logical grammars and BNFs work that you can check out your own examples. Here are some suggestions for grammars to check out:

Pick your favorite programming language (if you have one): Python we mentioned above, C is a popular low-level language, Prolog is a logic-based language.
A more complex AI example is description logic, which is a powerful KR language for designing knowledge bases.
The RFC for emails contains the BNF for valid email addresses. Check it out 🤓

Parsing

Now that we’ve formally defined what formal languages and their formulas are, let’s look at how computers (and also perhaps humans, subconsciously) read these formulas.

This happens by means of a process known as parsing, which is the step-wise reconstruction of formulas into their constitutive parts. Essentially, “unwinding” the formula, by figuring out how it was constructed.

This is the first step of how computers understand formulas (computer programs etc.) as it gives them a clear order in which to process its components. Later, when we’ll look into how the semantic processing of formulas works—how we assign meaning to them—this will become very important.

To illustrate the idea of parsing, let’s assume that our propositional language has just the three propositional variables p, q, r . We can then understand the grammar of this language as the collection of the following eight rules:

Essentially, this is a collection of eight rules:

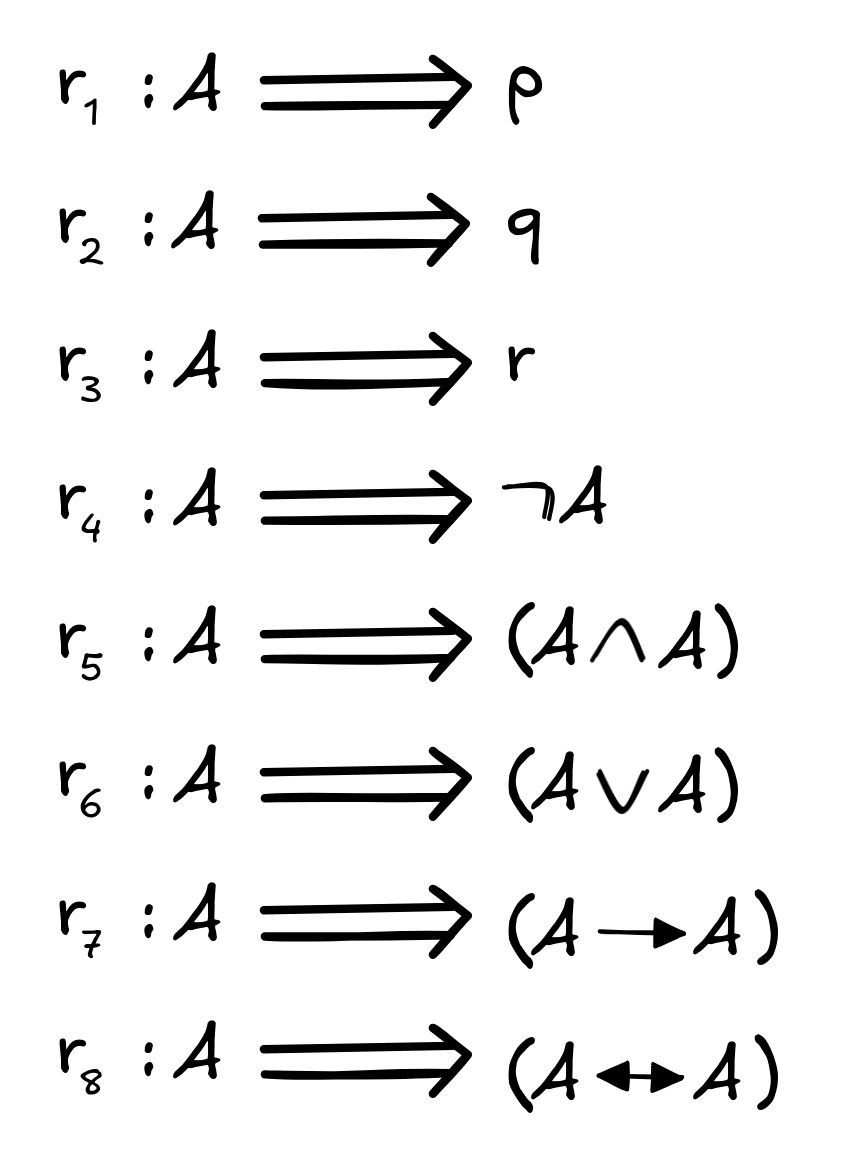
Rules like this are sometimes called rewrite rules. The intuition is that starting from the abstract ‘start’ symbol A , the rules allow you to rewrite A to any formula in the language. So, any formula in the language can be derived by applying a finite number of choices from these rules. For instance, to show that is a formula in this language, we start with A and, using the rules above, we rewrite this A until we arrive at this formula. We can do this in four steps:

To make this more insightful, we can turn this derivation into a so-called parse tree, which is a very useful representation of the syntax of a formula. A parse tree is a structure that is rooted in the abstract label A that forms the base of our BNF definition of the language. You can construct a tree by just following the derivation above, step by step. Each application of a rule introduces a new branching, until there is nothing left to do anymore. Here is how to construct the parse tree for the derivation we gave for . We start with a node A and then look at the derivation to see which rule to apply first. This is rule 4, which maps A to a new formula 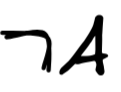. For each new symbol we create a new branch:

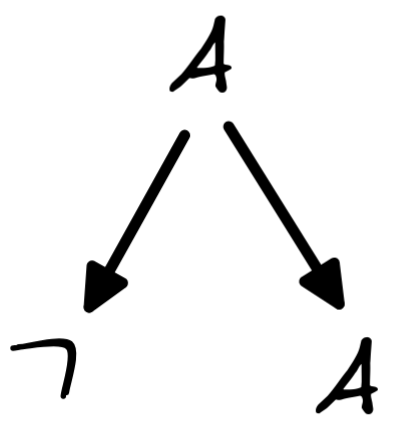
Then, we apply rule 5 to the right-most branch. This rule rewrites this A into (A\land A), which creates five more branches:

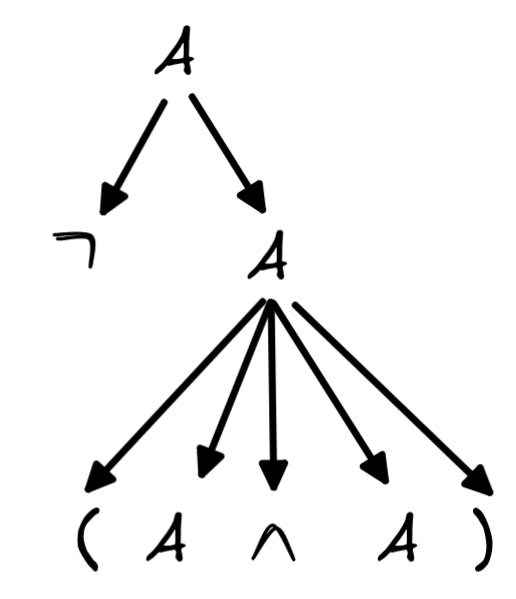
Then, we apply rule 1 to A that is to the left of “\land”:

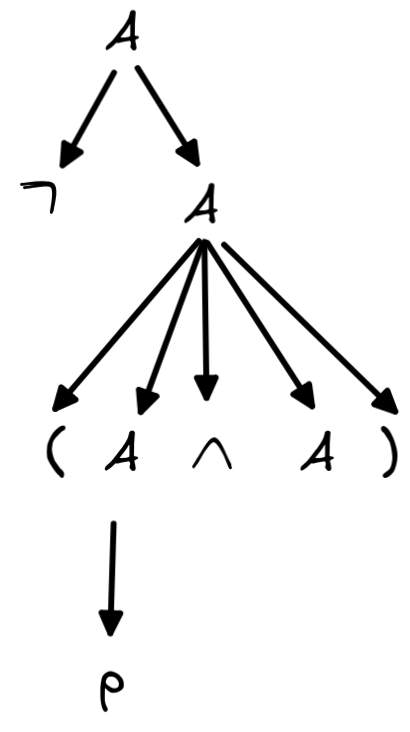
Finally, we apply rule 2:

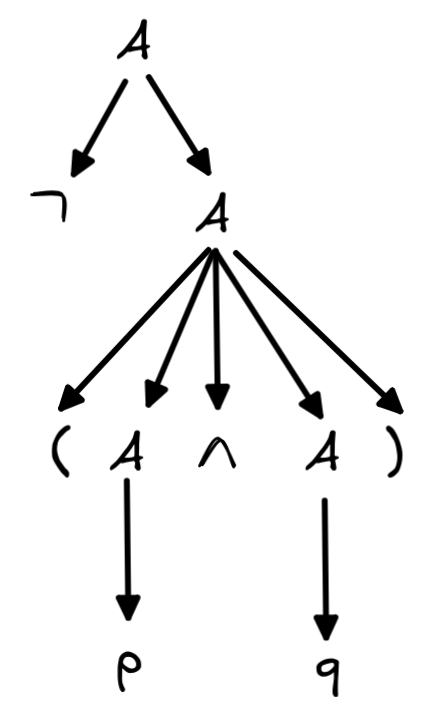
This now is the parse tree corresponding to our derivation of . The leaves of the tree spell out the formula, each branching is an application of a rule from the BNF grammar.

For a computer it is essential to be capable of parsing a complex formula in this way. This is because the parse of a formula gives us access to the logical form. Say, that the propositions in this logical language are meant to give a medical system crucial information about a patient. For instance, p, q , and r each correspond to the proposition that states that the patient has a certain symptom, call these symptoms P , Q , and R , respectively. If we feed the system the formula 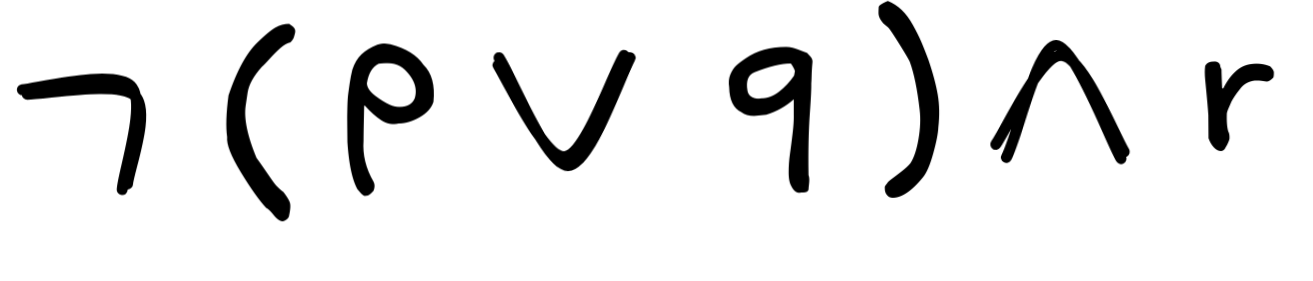, then we want the system to know that the patient is showing symptom R, but not showing P or Q . It needs to figure out that the sub-proposition , are negated, while sub-proposition r is not. To do this, it needs to parse the formula correctly. From the parse, it is clear that the disjunction is negated, but that r , escapes the effect of that negation.

Parsing allows us to distinguish seemingly similar, but crucially different logical forms like:

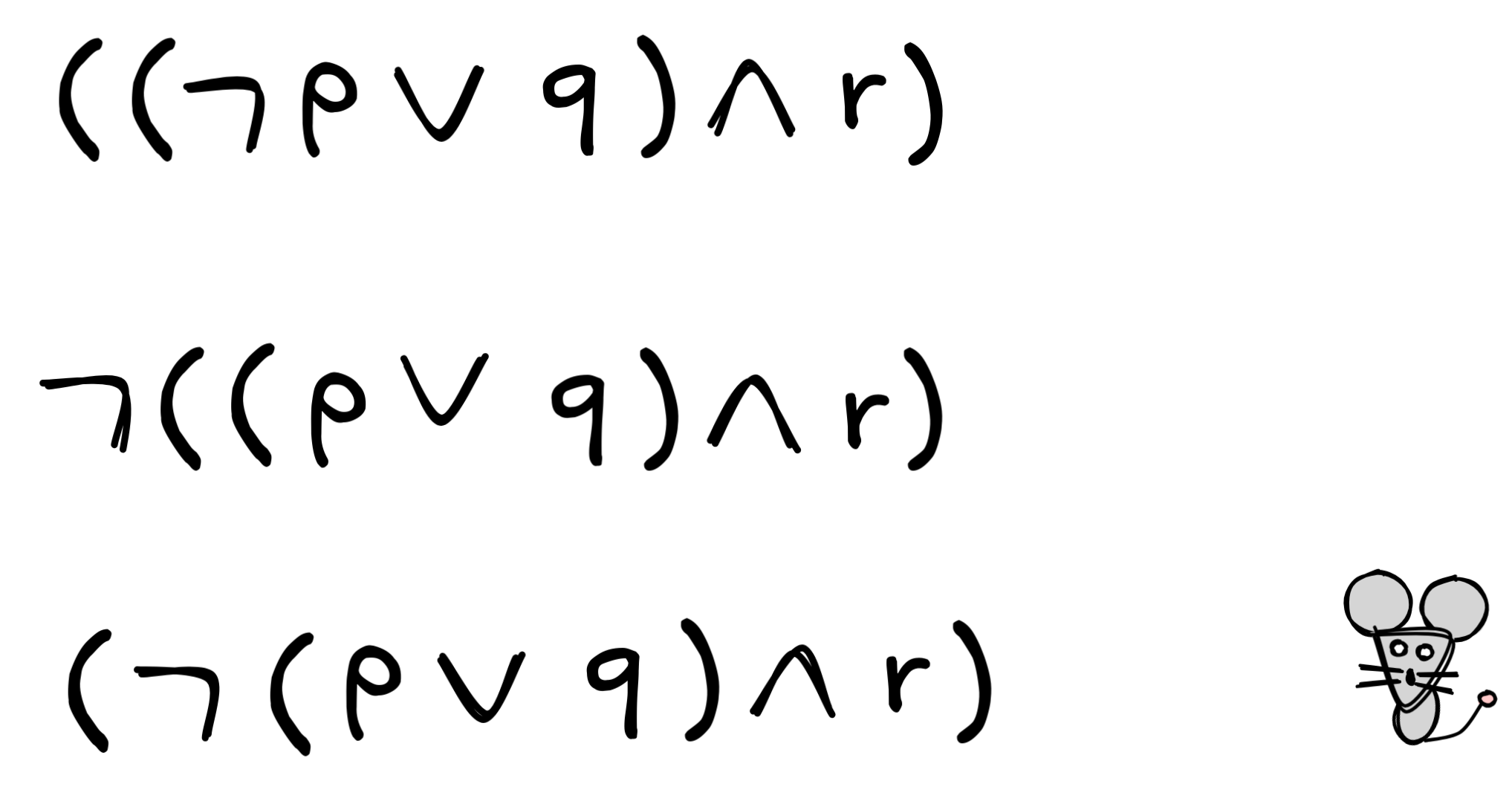
A fundamental insight of logical theory is that when a grammar is properly defined, we get what’s known as unique readability. A formula has this property when the grammar only provides a single parse tree for it. This is the case for the examples we gave above. For instance, for , we don’t have a choice in what rule to apply first when we start our derivation. We cannot for instance apply rule 4 before we apply rule 7. If we did, we would end up with a different formula. We do have some choices later in the derivation. For instance, after applying rule 4, we could have chosen to apply rule 5 to the A to the left of the . But that is not a choice that affects the structure. The parse tree would remain the same. In other words, all derivations of this formula lead to the same tree.

Unique readability is of the utmost importance since if it fails, this means that formulas are ambiguous. Since we said that avoiding ambiguity is one of the motivations for the use of formal languages, this means that we need to take special care in designing our grammar. Take the following grammar, for example (note the absence of parentheses in the conjunction case): In this language, we can derive the following formula: 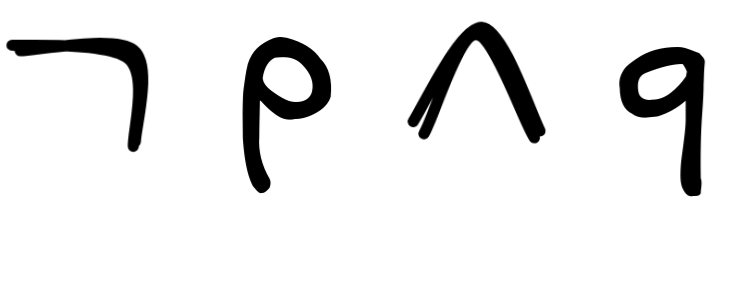. Crucially, though, we can derive this in two distinct ways, corresponding to the following two parse trees.

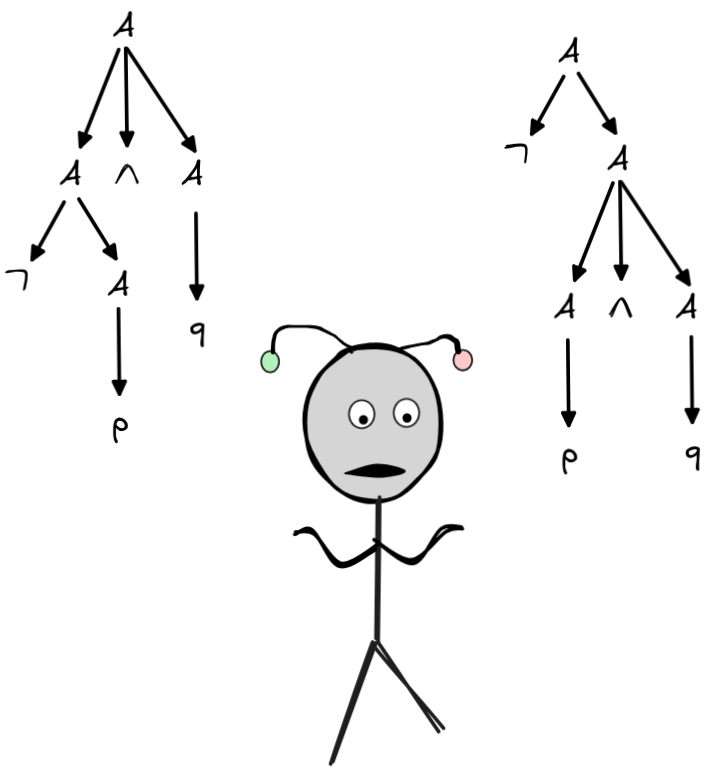
Imagine we are building an AI system to regulate a train crossing. There is a light stopping traffic from crossing the railway when it turns red and similarly there is a light indicating the train should stop and wait with crossing the road until that light turns green. Let’s say we have trained a neural network to regulate things as efficiently as possible, minimizing train delays and traffic jams. Unfortunately, the neural network is not flawless. We need a rule-based system to make sure the decisions made by the network are safe. To do this, we translate the network’s decisions to statements in a propositional logic and compare these to rules that we want the system to obey. Let’s say that p means that the cars have a green light and q means that the train has a green light. We now want a rule that says that p and q cannot be true at the same time.

As the two parse trees above show us, we have no way of doing this. If we state the rule as 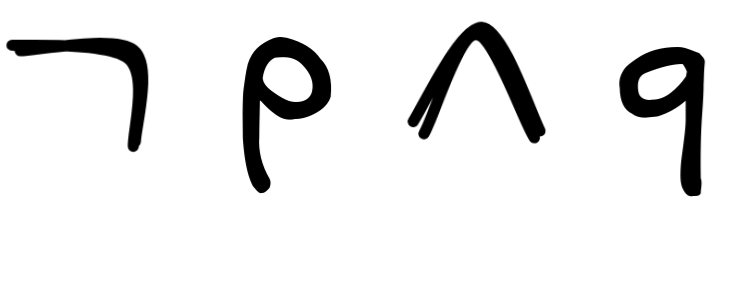, we end up with something that could be misunderstood. The two trees correspond to two distinct derivations, which correspond to two different structures for the same formula. In turn this means that the formula will have two interpretations. On the right is the interpretation that would be handy for this AI system: cars and trains do not have a green light at the same time. But if the system instead adopts the structure on the left, we could end up with a system that demands that trains have a green light while cars do not. Ambiguity might just have created a huge traffic jam! This shows that the BNF above is unsuitable as a formal language, since it fails the property of unique readability. All this is why we need to be careful about the auxiliaries, like , which ultimately guarantee unique readability.

Parsing is an incredibly important subject in the foundations and practice of programming, natural language processing (NLP), and elsewhere. We don’t have time to go into the details, but think of programming for a second. A programming language is essentially a tool to write down instructions for a computer in a human-readable way. What happens “under the hood” is that the computer translates the program you write into machine instructions (the proverbial 1’s and 0’s).

To ensure that the machine instructions really correspond to what you had in mind when you wrote the program, the computer needs to understand what you meant. Since a computer is deterministic and not particularly intelligent, the only way it can do this is according to unambiguous instructions about what means what.

But clearly, we can’t just write for each program what it means in machine instructions-otherwise, what’s the point of having the language in the first place? Instead, we specify what the individual expressions of the language mean and how combining them according to the grammar affects that meaning. In this way, we guarantee that for each program we could possibly write, we can translate it into machine instructions.

But to do so, we need to know which expressions occur in which order in the program. To determine this is the role of the parser. This shows the fundamental importance of parsing in programming and human-computer interaction.

Knowledge representation

The development of large language models for generative AI has made a significant impact on applications of AI. Because the interaction with such models involves the medium of natural language, generative AI has a serious ambiguity problem. For that reason, it is crucial for applications that require precision that there are rule-based components that avoid the problems inherent to natural language.

So, let’s talk for a moment about the role of formal languages in AI applications. We’ve already talked about the fact that programming languages are essentially just formal languages. So we can use the theory of formal languages to understand this crucial aspect of human-machine interaction. Formal languages, however, solve the problem of how to communicate with computers in a much more general way. Their potential to avoid ambiguity means that formal languages are essential to applications that require precision.

In Chapter 1. Logic and AI , we introduced so-called expert systems. These are systems where vast bodies of ’expertise’ in a certain domain have been translated into databases of formalised statements and (if-then) rules, in order to solve complex problems concerning the domain in question. In such systems, there are so many rules and facts that it is impossible for the human expert to keep track of everything.

Designing expert systems involves translating existing expert knowledge into a formal language that the AI expert system can work with. The process of translating a natural language expression into a formal language is known as formalization, which is a large part of the broader field known as knowledge representation.

The idea is that we can represent basic facts about the world using logical formulas of a suitable language and rules as if-then statements between such statements. To illustrate, let’s consider a toy example. Suppose that our friend IA is looking for an important letter, which should be somewhere around this desk with two drawers:

Suppose we have some information that we want to pass on to IA , who understands the language of propositional logic. Here are a few claims in natural language that we might want to convey, both in natural language and in the formal language of propositional logic, where we stipulate that LEFT is a propositional variable, which states that the letter is in the left drawer, and RIGHT is a propositional variable, which states that the letter is in the right drawer:

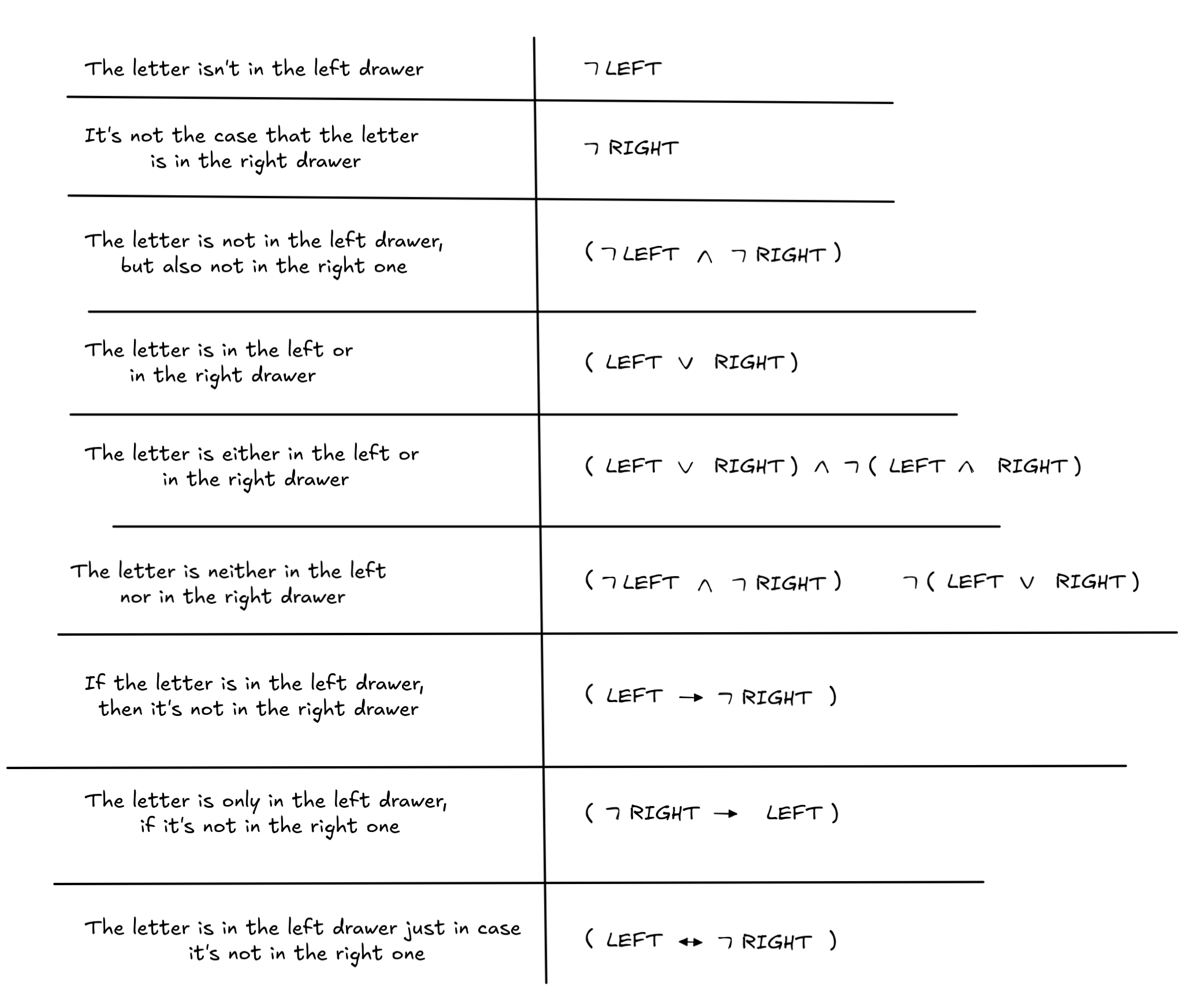
These examples can be a helpful guideline, but it’s important to keep in mind that formalization and knowledge representation is more of an engineering problem than a mathematical problem: there is not always an absolutely right or wrong answer (even though some cases are clearly right/wrong), it depends on the purpose of the formalization, on the reasoning context, and other factors what is a good or bad formalization.

Already the choice of language can be a difficult decision. We need to evaluate a language’s expressive power against the additional complexity that comes with that. Sometimes, simple languages, like the language of propositional logic, are the right choice, sometimes we need more complex languages.

Once we’ve formalized our claims in a suitable formal language, we collect our formalized knowledge in what’s known as a knowledge bas (KB). Generally speaking, a KB is a way of storing formalized knowledge in such a way that any agent—artificial or otherwise—can both ask the KB what is already known or tell the KB new facts. From a logical perspective, it turns out, that we can then think of a KB as simply as set of formulas of a suitable language.

An expert system can generate unknown novel facts on the basis of a great many applications of modus ponens and other patterns of valid inference. Conversely, expert systems could be used to answer queries. This means that a user prompts the system with a certain proposition (standing for some statement in the domain of expertise) and the expert system would then search for a chain of inferences either leading to that proposition or to its negation. Ultimately then, the expert system can help the user understand whether something relevant to the domain of expertise is true or not, and also why that conclusion can be drawn.

The concept of a KB is one of the fundamental concepts of the AI discipline known as Knowledge Representation and Reasoning, and will accompany us throughout the course

Currently, the term ’expert system’ is not used a lot anymore. However, rule-based systems are still very popular applications of formal languages in businesses and research in systems such as WolframAlpha. They are (relatively) cheap to build and, importantly, they are fast and reliable. As we hinted at above, they are also fully transparent, meaning that an expert system doesn’t just solve a complex problem, it can also provide a detailed explanation of how it came to the solution, since it can show you the rules and facts it used in order to reach it.

This is in stark contrast to generative AI, which relies on untraceable statistical regularities in vast amounts of data. This lack of traceable reasoning makes the reliability of generative AI questionable, thereby raising question about its safe use. Even worse, it makes it less clear that AI can be held accountable for the decisions it makes.

Formal languages

Formal vs. natural languages

Ambiguity

Over-expressiveness

Formal languages

Sets

Alphabets

Grammar

The language of logic

Parsing

Knowledge representation

Further readings