By: Johannes Korbmacher

Logic and AI

Logic and AI are intimately connected. In this chapter you’ll learn how.

At the end of the chapter, you’ll be able to:

define logic and artificial intelligence as scientific disciplines,
explain the three main ways in which the two disciplines are related, and
give some examples of uses of logical methods in AI and distinguish them from non-logical methods.

By the way, meet IA (read: “for all I”)!

It is our friendly course mascot, and will feature in many of the examples and exercises.

What is AI?

The term “artificial intelligence” (AI) is used in different ways. Sometimes we mean by it intelligence which is artificial. That is, we think of AI as an ability that computational systems (≈computers) can have or not. This is, for example, how Wikipedia defines AI in the first place (read the first sentence of the article). In this sense of the term we can ask, for example, whether “true” AI is possible.

Sometimes, by AI we mean a specific technology or set of technologies. In recent societal discourse especially, “artificial intelligence” has become virtually synonymous with generative AI (GenAI) and its various applications. This is the sense of AI in which ChatGPT, Copilot, Gemini, Claude, Grok, Llama and DeepSeek are AIs. In this sense of the term, AI is not only possible but real: these technologies exist (obviously)!

There is also a sense of AI as AI-engineering, which is concerned with the practical details of designing, optimizing, and realizing AI technologies. This is the sense of AI when somebody says that they “work in AI”.

In yet another sense of the word, AI is a scientific discipline. It is not easy to define this discipline in simple terms—when you think about it, most scientific disciplines are actually quite hard to define—but as a first shot we can say that AI aims to understand, artificially replicate, and possibly improve intelligent behavior.

AI in this sense is a rather multifaceted discipline. Clearly, computer science plays an important role in AI as it studies computation and automation and the main (and perhaps only?) method for artificially replicating intelligent behavior is by automated, computational models—i.e. computer programs.

But AI is not only computer science. Understanding intelligent behavior is also a core objective of psychology. Thinking about what it means to have (artificial) intelligence (in the capability sense of the word), whether it’s possible to have true artificial intelligence, and so on are important questions in philosophy, especially the philosophy of mind.

The special role of language for thought—illustrated, for example, by Fodor’s language of thought hypothesis —shows that also linguistics plays a role in AI.—In short, AI is highly interdisciplinary field of study.

All of these senses of AI will play a role in this course. For example, we’ll look at the role that logic plays in intelligent behavior, the role of logic in AI technologies, and the relationship between logic as a discipline and AI.

What is logic?

So, what is logic, then? Well, as a discipline, logic is the study of valid reasoning. Let’s talk about what that means.

The basic concept of logic is that of an inference (sometimes “argument”), which is a simple piece of reasoning like the following:

All humans are mortal and Socrates is human. So, Socrates is mortal.
All swans we’ve observed so far were white. Therefore, all swans are white.

You’ve almost certainly come across these examples if you had any contact with philosophy or argumentation theory or the like.

To talk about logic and validity, it’s helpful to introduce some technical terminology. In an inference:

The conclusion (sometimes “consequence”) is what’s being inferred.
The premises are the assumptions or hypotheses that the conclusion is based on.

So, in the first inference, all humans being mortal and Socrates being human are the premises, and Socrates being mortal is the conclusion. In the second inference, all swans observed so far being white is the premise, and all swans being white is the conclusion.

Typically, there are some linguistic hints that allow you to identify premises and conclusions. Phrases like “so” and “therefore” are inference indicators. The conclusion typically follows them, though it can be the other way around. Take the inference indicator “since”, for example, and look at how we use it in the following inference:

The ground is wet since it’s raining and if it’s raining, the ground is wet.

Similarly, the premises typically precede any inference indicators, but as in our example can also come after. There are also premise indicators, like the “given that” in the following mathematical inference:

Given that this figure is a triangle and the sum of all angles in a triangle is 180°, we can conclude that the sum of all angles in this figure is 180°.

By the way, here “we can conclude that” is the conclusion indicator.

Once we’ve identified the logical structure of an inference, we often represent it in a visually clear way. For example, IA uses the so-called inference line to indicate the inferential structure here:

There are many different notations. For example, in mathematics, we often use the turnstile \vdash to indicate a (valid) inference and commas to separate the premises, like so:

The robot cat next to the inference is IE (read: “there is”), which is IA ’s pet.

With an inference comes the expectation that the premises support the conclusion, that the conclusion follows from the premises. An inference where this is the case is a valid inference.

The first inference—the one about Socrates’ mortality—looks pretty solid. If all humans are mortal and Socrates is human, then he must be mortal. In logic, we call an inference like that, where the premises necessitate the conclusion, deductively valid. Deductive inferences are the traditional topic of most logical theory. They are often associated with mathematical reasoning.

But what about the second inference—the one about the swans. Even if all the swans we’ve observed were white, it’s certainly possible that there’s a non-white (robot?) swan—just that we haven’t seen it yet. So, the inference from all previously observed swans being white to all swans being white is not deductively valid—it is deductively invalid.

But isn’t there a sense in which the fact that all the swans we’ve observed were white does support the claim that all swans are white? Now, we know that there are black swans, so let’s take slightly modified inference. Suppose that there are a hundred marbles in this bowl. We can’t see inside the bowl and we can only take the marbles out one by one. We keep taking out marbles and they are all white. We’ve sampled the marbles randomly, we’ve taken them from the bottom of the bag, from the top, and so on. They’re always white.

After some time of sampling—but before we’ve sampled them all—it would seem reasonable to conclude that all marbles are white. It might be debatable when exactly this point is—after 50, 70, 80 white marbles—but it seems rather clear that at some point, we can reasonably conclude that all marbles are white. Not with certainty—a black marble might still be in there somewhere—but with reasonable confidence.

The point is that for some number of marbles, for argument’s sake let’s say 70, the fact that we’ve samples 70 white marbles together with the assumption that we’ve sampled well (to avoid selection bias and the like), supports the conclusion that all marbles are white by making it more likely. An inference like this—where the premises make the conclusion more likely—is called an inductively strong inference. In this context, the strength of the inference is determined by how much more likely the conclusion is given the premises: the inference from 90 white marbles is stronger than the one from 70 white marbles.

So, this is, in essence, what logicians study: different notions of “good” inference, ways in which the premises can support a conclusion. We’ve already seen a kind of classification emerging, which we’ll study in more detail:

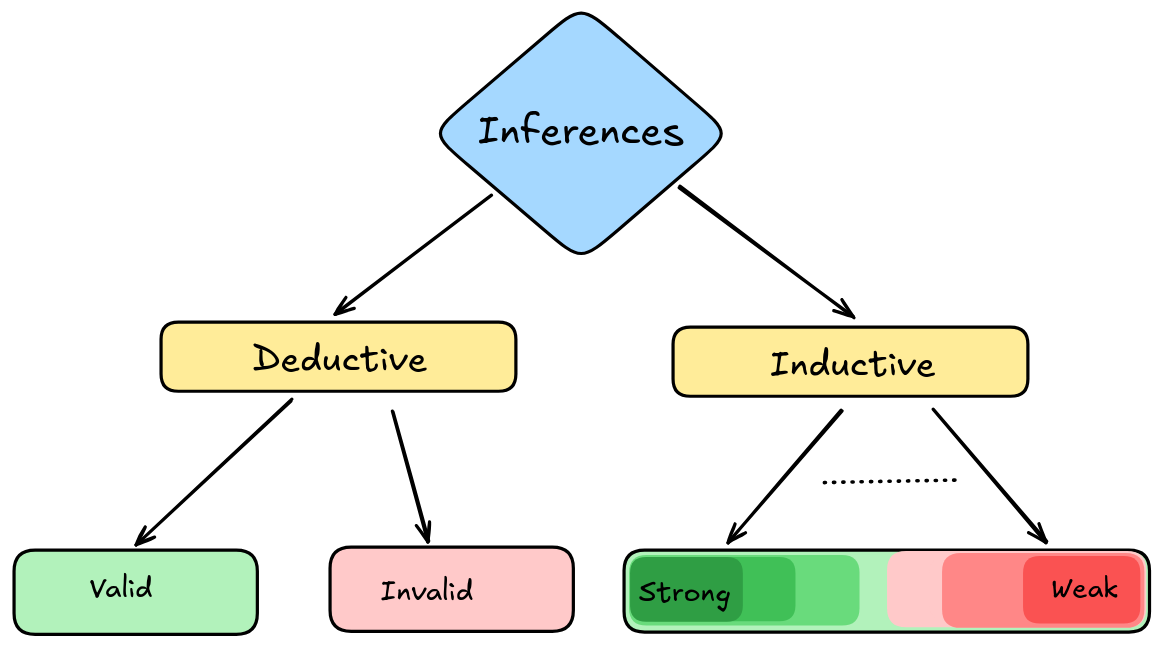
Note that logicians (qua logicians) don’t study how people actually reason (psychology of reasoning), or how to use arguments to convince others (rhetoric), or things of that sort. These are all good to know, of course, but they are not the main interest of logicians.

Logical systems

Just like with the term “artificial intelligence”, the term “logic” is used with different meanings. What we’ve looked at so far is the academic discipline of logic. In this context, we might say that an inference is “logical” and mean that it’s valid (or inductively strong). This is in contrast saying something like “it’s logical that I was scared”, which means something like “it’s understandable that I was scared”.

But there’s also a common way of speaking of “someone’s logic”, as in “according to your logic, we should go home”. This points to an important aspect of logical theory, which we’ll need to talk about before we can move to the relationship between logic and AI: the existence of different logical systems.

What we mean when we say that “according to your logic we should do the thing” is something like “according to the system of premises and inferences you accept, we should do the thing”. It turns out that this sense of logic, we also find in logical theory.

Logicians approach the study of valid inference the way most scientists approach their subject matter: using mathematical models. We call the models that logicians use to study valid inference logical systems.

A logical system typically has three components:

a syntax, which is a model of the language of the inferences,
a semantics, which is model of the meaning of the premises and conclusions,
and a proof theory, which is a model of stepwise inference.

Together, these three components provide a mathematical model of valid inference. Throughout the course, you’ll learn more about syntax, semantics, and proof theory by studying how they are used in different AI applications. By the end, you’ll have a good idea of what the different components of logical systems do, and how they work together to provide a comprehensive model of valid inference.

In essence, logical systems are not all that different from the mathematical models used by physicists, for example. To illustrate, think about how a physicist would approach the question of how far IA can throw its ball:

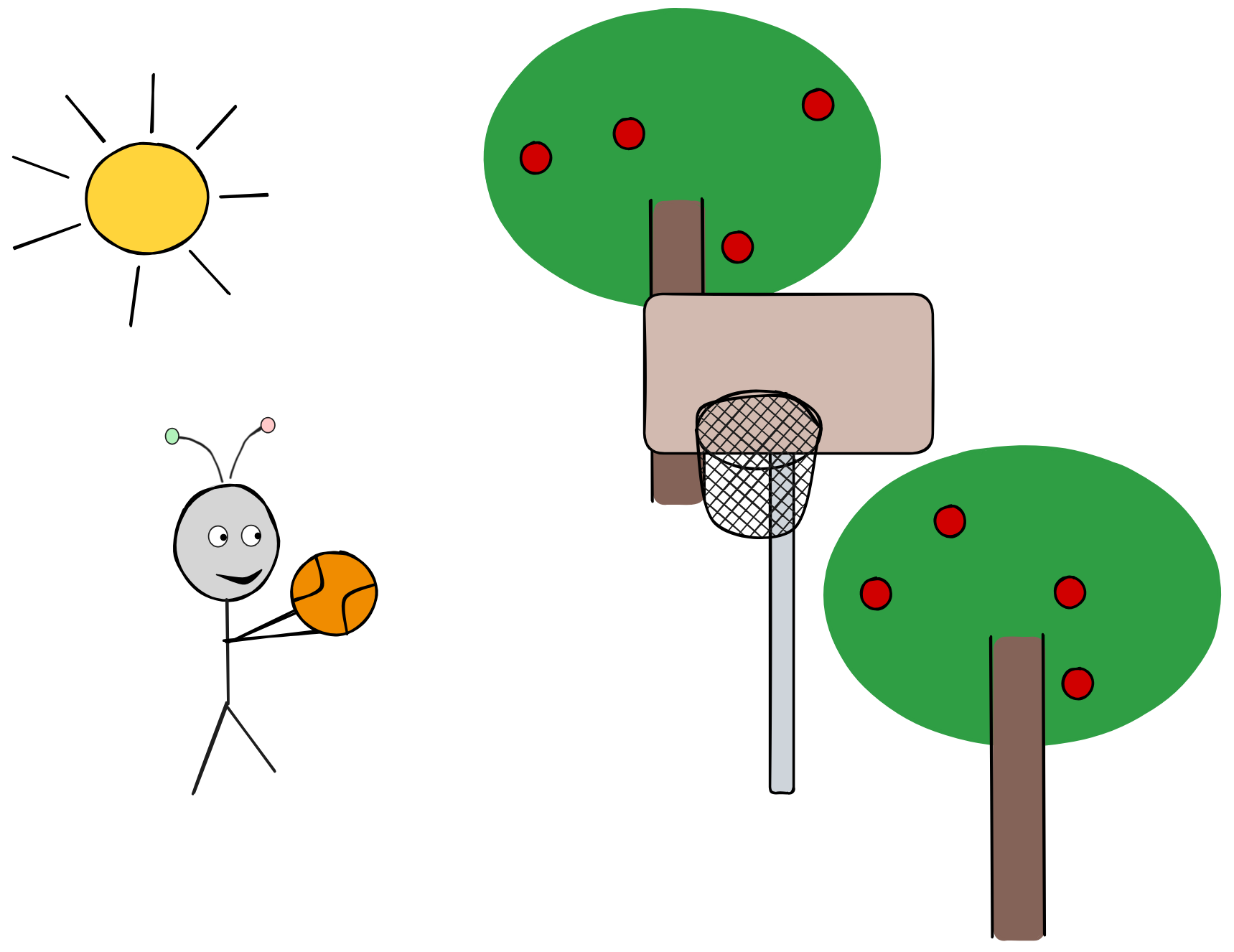
The physicist might use Newtonian mechanics to predict how far the ball will fly, but they wouldn’t apply the laws of mechanics directly to the real world. First, they’d build a mathematical model of the situation, which looks something like this:

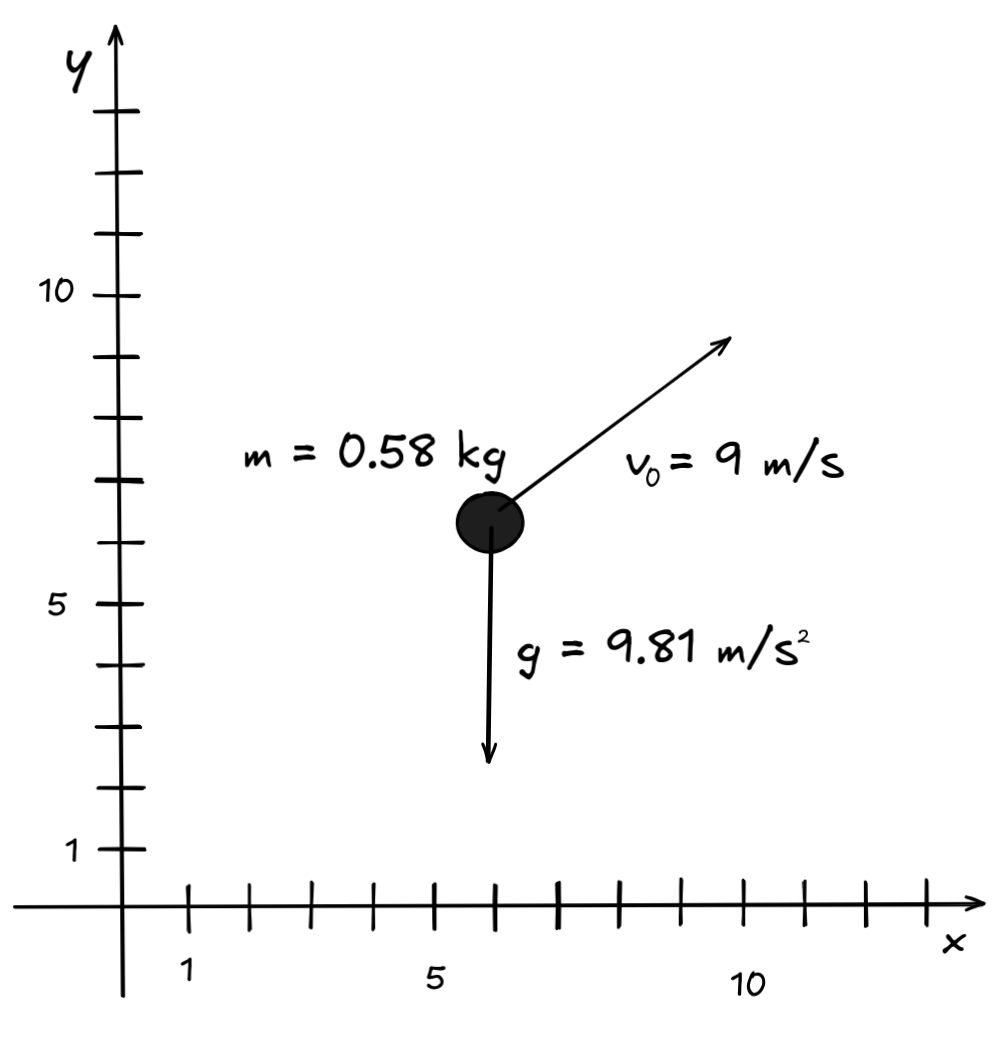
In this model, the physicist would assign a mass to the ball, represents the ball as a point in 2-dimensional Euclidian space, and treats the forces acting on the ball as vectors. Assuming that there’s no air resistance, it’s a high-school level exercise to calculate where the ball will land using the laws of classical mechanics (can you still do it?).

What’s characteristic of mathematical models is that they abstract away from irrelevant features of reality (ignoring the trees, for example), they idealize the situation (by treating the ball as a point-mass, for example), and they introduce simplifying assumptions (such as no air resistance, for example). Ultimately, this is what makes it possible to apply exact mathematical calculations to a real-world scenario like ours.

Logical systems work in just the same way as our physicist’s model: they involve abstractions, idealizations, and simplifying assumptions in order to allow us to make exact mathematical calculations about valid inference:

Syntax introduces the ideas of a formal language and of logical formulas, which are abstract representations of the logically relevant structure of premises and conclusions. This is roughly analogous to the way the physicist represents the ball as a point-mass in a coordinate system, and the forces acting on the ball as vectors, etc.
Semantics introduces the idea of formal models, which are representations of meaning, spelled out in the context of formal languages. These models allow us to study logical laws, which are roughly analogous to the laws of mechanics, such as:

F = m x a
Interestingly, formal models often involve simplifying assumptions, such as that every sentence has a determinate truth-value from either true or false.¹
Finally, proof theory introduces the idea of formal derivations, which are a model of stepwise valid inference. Just like the physical model calculates where the ball will land using the laws of mechanics, these derivations calculate valid inferences from the basic laws of logic.

Developing and studying logical systems is the core business of logical theory and has lead to rich body of logical knowledge.

One last thing to note about logical systems is that there are many of them. In this course, you’ll learn about a wide range of logical systems and how they are used in AI. So, there’s what we might call logical diversity!

There are different ways of classifying logical systems, but let’s just just look at two to get the point of logical diversity across.

One natural way of classifying logical systems is by the kind of inferences they deal with. For example, there are systems that deal with:

grammatical conjunctions, viz. propositional logic,
quantifiers, viz. predicate logic,
modals, viz. modal logic.

Another way of classifying logical systems is by their background assumptions/philosophies. For example, there’s:

classical logic, which assumes (among other things) that every sentence is either true or false,
intuitionistic logic, which assumes that truth needs to be “constructed”,
paracomplete and paraconsistent logics, which allow for exceptions to certain classical logical laws, such as that there’s no true contradiction.

As you’ll see different systems are useful in different contexts.

Logic and AI

Logic plays a special role in AI since its inception as an academic discipline in the second half of the 20th century. One event that is often mentioned as a “beginning” of AI is the 1956 Dartmouth Summer Research Project on Artificial Intelligence, which was organized by Claude Shannon, John McCarthy, Nathaniel Rochester, and Marvin Minsky and who are therefore considered by some the “founding fathers”. The research proposal contains for the event one of the first documented uses of the term “artificial intelligence” to refer to an academic discipline.

The naming of the discipline is typically attributed to McCarthy, who thought that logic is the path to achieving human-level artificial intelligence (in the ability sense of the term). But we don’t need to think about human-level intelligence to understand the relevance of logic to AI research. An insight typically attributed to Claude Shannon in his master’s thesis is that we can think of the behavior of electrical circuits (specifically relays) in logical terms.

To illustrate the idea, take this simple circuit with two switches, A and B:

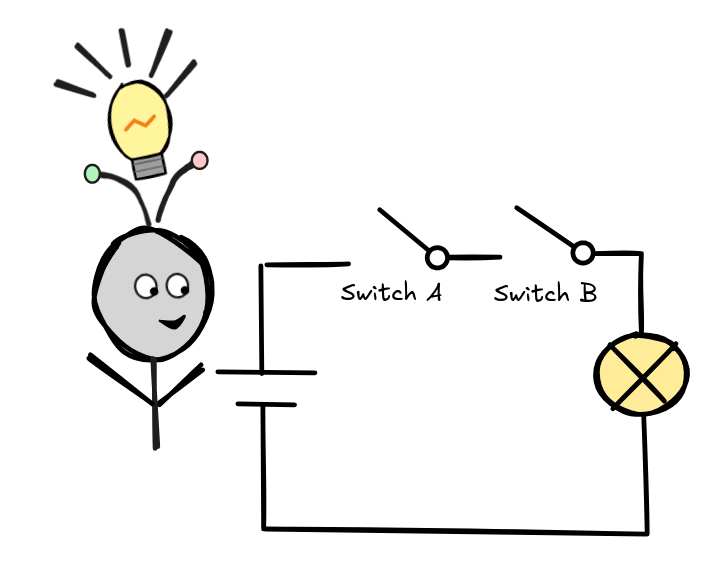
If—and only if—both A and B are flipped, the light turns on. Shannon realized that this is effectively the operation of logical conjunction from Boolean logic: Think of a switch being flipped “on” as 1 and it being switched “off” as 0. Similarly, take the light turning “on” to be 1 and it being “off” as 0. Then the behavior of the circuit is to return 1 just in case both A and B are 1 and 0 otherwise—which is just the operation of logical conjunction from Boolean logic.

This relates logic to circuits, but what does this have to do with AI? One way of making the connection is to widen our understanding of “intelligent behavior” from human intelligence to something that allows us to think of a circuit like the one above as a reasoning, intelligent agent. The idea is that we can reconstruct the behavior of the circuit as an inference from two statements—A and B, which we take to mean that the respective switches are “on”—to an action being carried out—turning on the light, which we can think of as yet another statement, L. So the circuit in a sense performs an inference: it infers L from both A and B.

Widening our understanding of intelligence like this allows us to study the behavior of sliding doors, AC systems, self-driving cars, and much more as AI systems using logic. This is a very powerful idea.

The thought that logic is the path to achieving human-level artificial intelligence is the paradigm of logic-based AI, which was the dominant paradigm for AI research from the 1950 until at least the late 1980s. Around this time, probability theory and statistics slowly started to take over as the main approach to the problems of AI, putting the focus on ideas like machine learning and big data.

The success of this approach is not in small part due to artificial neural networks (ANNs), which are, effectively, statistical models of data, obtained through machine learning on an architecture that is inspired by the structure of the human brain. Today, statistics-based AI using XAIs is, by far, the dominant paradigm in AI research. This is the approach that led to the recent developments in GenAI.

To understand this shift, it’s helpful to look at the various ways in which logic and AI are related. On a very general level, we can distinguish three ways in which logic is relevant for AI research: there is a foundational, methodological, and auxiliary entanglement between logic and AI research.

Foundational

Valid inference simply is paradigmatic intelligent behavior. So, logical systems directly target what we’re trying to model in AI—logical systems are models of intelligent behavior. So, by our definition, logical systems are part of AI. This makes logical part of AI and the results of logical research qua logical research relevant to AI research.

The relevance of logic in this sense is mainly foundational, meaning that logic contributes to the understanding of (one of) the basic concepts of AI. A part of logical theory that’s particularly relevant here is metalogic, which deals with the limits and possibilities of logical systems in principle. What’s particularly interesting about this is that metalogical research is, more or less, research in pure mathematics, which turns out to be highly relevant to practical questions in AI research.

Here are two famous metalogical results that (some) people think are highly relevant to AI research:

Gödel’s (first) incompleteness theorem, which implies that for every logical system that is free of internal contradictions and models basic mathematical reasoning, there is a mathematical statement that is undecidable in the system, meaning that the statement can neither be proven nor refuted in that system.

Many researchers, including Gödel himself, have thought that this has deep implications for AI. The arguments here are rather subtle and without going into the very technical details of Gödel’s result it is very easy to make mistakes, but a very rough version of the argument runs as follows:

Since the human mind is consistent and capable of mathematical reasoning, but there is no in principle undecidable mathematical fact for the human mind, Gödel’s result shows that the human mind cannot be modeled or replicated by a logical system.

If this is correct, it dooms a wide range of approaches to AI, including logic-based approaches discussed.
Church and Turing’s undecidability theorem, which entails that validity in the standard system of predicate logic is (algorithmically) undecidable, meaning that there is no algorithm and there can never be an algorithm that correctly determines in finitely many steps whether any given inference in the system of predicate logic is valid.

This result seems to show directly that we cannot “fully automate” validity checking using AI and maintain absolute reliability.

The relevance of logic to AI in this sense is hard to deny. At the same time, a young engineer setting out to change the world with AI, might think of logic in this sense as just theory with little practical relevance. But it’s important to keep in mind that it can be very helpful to know the limits and in principle possibilities of an approach before you start investing a lot of time and effort. Otherwise, you might try to solve a provably unsolvable problem.

Methodological

Historically, perhaps the most lasting influence that logic has had on the development of AI is via the logic-based AI paradigm, which is also known as symbolic AI due to its use of transparent, human-readable methods.

The idea that logic is the path to achieving human-level artificial intelligence has led to the development of many important technologies, both on as abstract designs and concrete technologies, such as the LISP programming language.

The technology which has had arguably the most influence within AI to come from the logic-based paradigm are the so-called expert systems, which are computer systems designed to behave like human experts at certain reasoning or decision making tasks. Examples of expert systems that found “real world” applications include Mycin, which is a system for medical diagnosis, and XCon, which helped selecting computer parts for your new gaming PC.

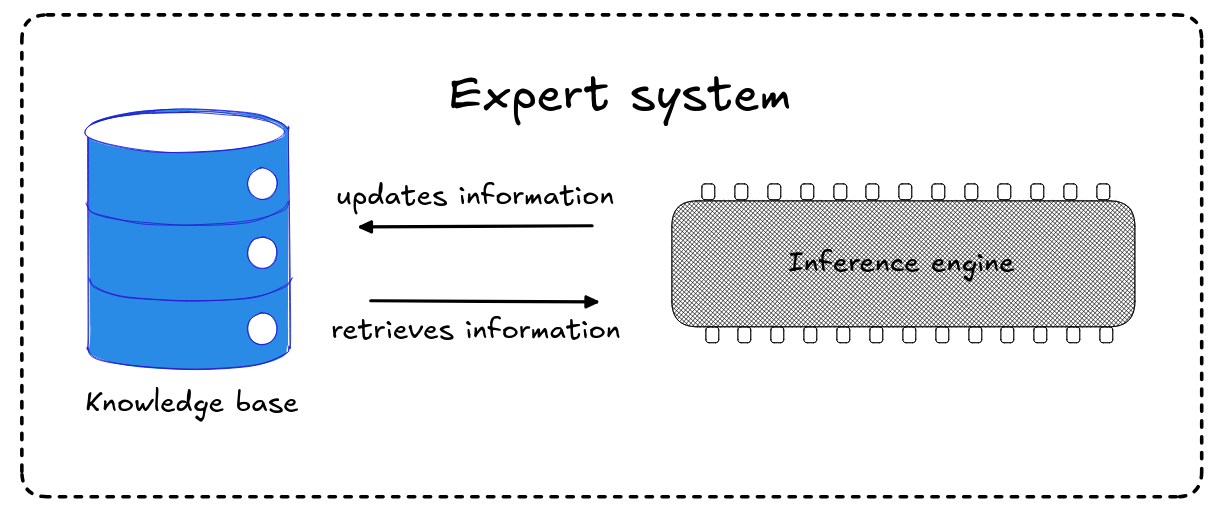An expert system (typically) has two components:

a knowledge base (KB), which stores the expert information and known facts, and
an inference engine (IE), which derives new information/decisions from input using the KB and valid inference.

Typically, the information in the KB takes the form of if-then rules. To An exper system for medical diagnosis, for example, may contain the following rule:

If the patient has a runny nose, a sore throat, and a mild fever,
then the patient likely has a common cold.

If we present the system with the known fact that our patient does have a runny nose, a sore throat, and a mild fever, the inference engine could easily derive that the patient likely has a common cold. If some symptom is missing, say the patient doesn’t have a fever, the engine can no longer validly infer that the patient has a cold—it could be something else.

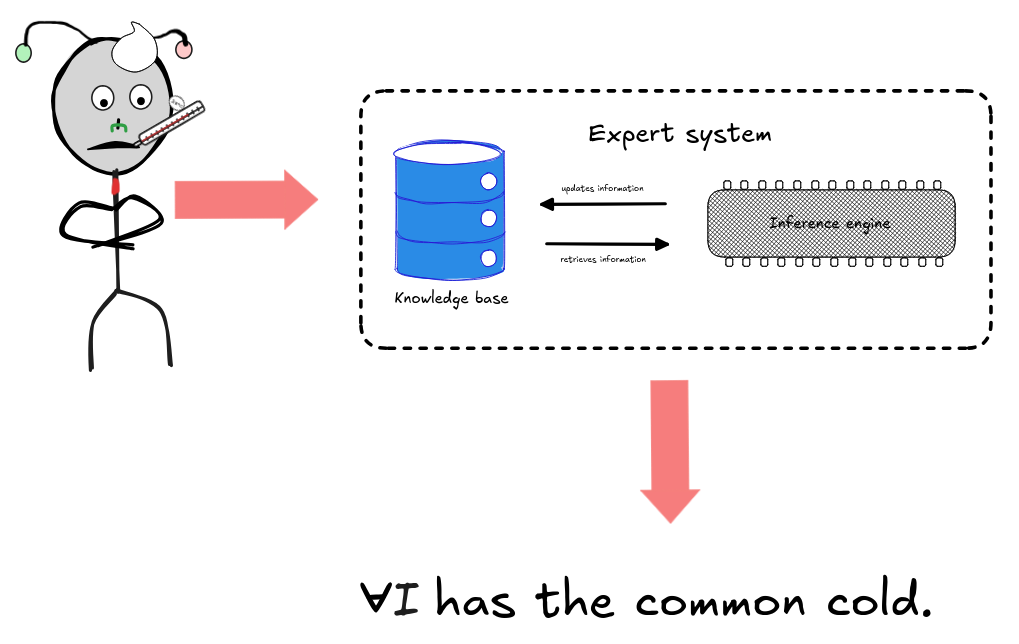
One major advantage of expert systems—especially in hindsight, compared to modern statistics-based systems—is that their decisions, predictions, recommendations, … are explainable. In our case of the common cold, for example, we can explain why the system predicts that IA has the common cold: because the robot presents the symptoms and there is a corresponding rule for the symptoms. This is typically very different with XAI-based systems, for example, where it’s not always possible to say why the system makes the predictions it does, making them “black boxes”. This has lead to development of the field of explainable AI (XAI), which tries to resolve the black box problems for statistics-based AI systems. The problem simply doesn’t occur for most logic-based systems.

So, why did the paradigm shift from logic-based AI to statistics-based AI?—The full (hi)story of this shift is nuanced and complicated, but looking at aspects of in a slightly simplified fashion may still help us understand the rather complex entanglement between logic and AI research.

We can identify at least two factors that contributed to the shift. One is the failure of logic-based systems to deliver on their promises. And the second one is the success of statistics-based systems with problems that logic-based systems failed to solve.

The “failures” of logic-based systems are themselves a complex topic, but we can illustrate at least some of the issues with a simple anecdote reported by Laërtius. According to the anecdote, Plato once defined a human as a featherless biped, much to the approval of everybody in the agora at the time (which is where the cool kids hung out). Along came history’s first punk, Diogenes, and presented Plato with a plucked chicken, remarking “Behold, Plato’s human.”

This seemingly unrelated anecdote from the history of philosophy illustrates a very relevant problem for logic-based AI systems: identifying the precise conditions under which concepts apply can be incredibly hard—even in seemingly simple cases (being a human) and even for clear experts (Plato was at the forefront of scientific research in his time, and he certainly could identify humans).

Plato’s definition seems to give us the following if-then rule:

If something's a featherless biped, then it is human.

Diogenes presents us with an object that satisfies the two conditions in the if-part of the rule, but not the condition in the then-part. He found a counterexample to Plato’s definition. We can easily imagine this kind of situation happening with expert systems, where the expert knowledge is expressed in similar if-then rules and the AI-system make corresponding classification errors by rigidly applying these rules. Fixing systems in light of such errors is a tedious process, which cannot easily be automated and requires further expert input: finding correct if-then rules often requires a lot of effort, trial-and-error, fine-tuning, etc. and then maintenance, bug-fixing, and so on.

Moreover, each problem (medical diagnostics, computer assembly, identifying humans, …) requires its own expert knowledge and expert system. Correspondingly, in general, we can’t expect the solutions to problems for one expert systems to transfer to the problems of another system.

These are some of the issues with expert systems that lead to development of such systems slowing down over the years, and ultimately halting during the (second) AI winter.

Logic-based AI achieved great things: IBM’s Deep Blue, which beat world chess champion Gary Kasparov in the 1990s, is ultimately a rule-based expert system and one of the main success stories of symbolic, logic-based AI. It shows how human-level—even super-human—intelligence can be achieved using logic-based expert systems. At the same time, logic-based methods struggled to generalize to more applications.

One example, which contrasts well with the achievement that is Deep Blue, is the case of Go. Developing an AI that performs at expert human, let alone super-human, levels in this game was generally considered out of reach for logic-based systems.

This changed with DeepMind’s AlphaGo, which is a XAI-based AI that’s been trained using statistical machine learning methods on large sets of game data. In a series of highly publicized events in the mid 2010s, AlphaGo managed to beat professional Go players at the highest level, suggesting the superiority of XAI over expert systems for beating games.

The success of statistics-based systems like AlphaGo at solving problems that logic-based systems have struggled with for a long time is another factor in the paradigm shift from logic-based to statistics-based systems. The comparison between Deep Blue and AlphaGo is instructive, but the success of statistics-based AI really is “across the board”: image recognition, translation, text-generation, …. In fact, statistics-based methods are at the heart of the recent developments of GenAI.

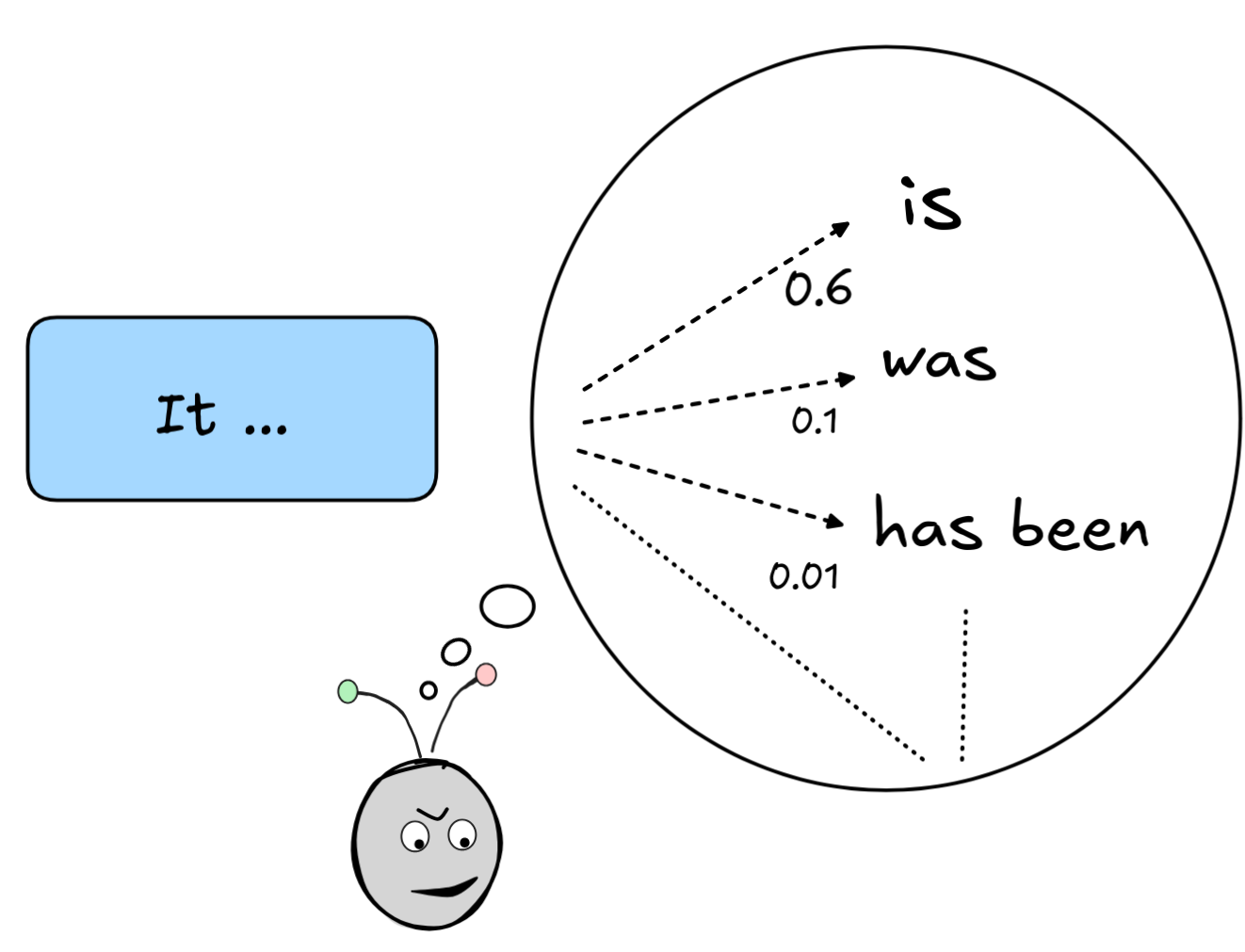
The statistics-based approach uses machine learning to train its systems. In contrast to expert systems, we no longer need to hard-code the relations between different facts, but the system learns these relations from the data. Rather than if-then rules, statistics-based systems typically use conditional probabilities to make predictions. For example, when a chatbot like ChatGPT or Claude answers a prompt, this essentially works by the underlying model repeatedly predicting what’s the most likely next piece given or conditional upon the prompt and text that’s already been generated, and then printing this most likely piece of text. This works impressively well.

It’s important to note, however, that it can be very hard to extract the learned rules from a statistics-based model: the models are, generally speaking opaque. This is in part because of the size of the models—the language models that underpin chatbot-technologies have literally billions of parameters—and in part because of the way the machine learning algorithms work.

Auxiliary

While statistics-based methods are, at the moment, the state of the art, logic still plays an important role in AI research. Logic-based research in AI has sparked the development of extremely sharp and powerfull tool for different tasks in AI development, which are still in use today.

One big area where this is the case is what’s known as Knowledge Representation and Reasoning (KRR). While subsymbolic systems, especially GenAI-systems like ChatGPT, can store factual information, they are—at least in the current state of the art—fairly unreliable with hallucinations being one of the main issues. If we want to have 100% recall of the stored information (think: your bank account, passwords, …), we need to use databases. Roughly, the difference between using a subsymbolic model to store information and using a symbolic model is the difference between trying to remember the information and writing it down. The connection between databases and logic is very deep: Codd’s theorem shows that querying a database is, in many cases, essentially just a special way of evaluating the formulas of the logical system of predicate logic.

KRR is just one example of where a logical tool is useful outside the scope of expert systems, and symbolic AI in the narrow sense of using logic as the sole foundation for AI. During the course, you’ll see logic is (almost) everywhere in AI, ranging from low-level transistors via high-level programming languages to the abstract study of AI’s abilities—all of this has to do with logic. Logic is, to this day, one of the main auxiliary disciplines of AI research.

The way forward

In recent developments and ongoing AI research, logic and logic-related topics are starting to play a significant role again.

The last years have seen the meteoric rise of GenAI systems, and especially large language models (LLMs). These are subsymbolic AI systems that are essentially large-scale probabilistic models of natural language. Under the hood, LLMs are neural networks with billions of parameters that are trained on huge sets of textual data using advanced machine-learning technologies. These neural networks approximate textual probabilities which estimate the likelihood of an expression being the next expression given a sequence of previously processed expressions.

LLMs have the impressive ability to mimic human language behavior. LLMs are the underlying technology of chatbots, like ChatGPT, who interact with humans by generating text responses to prompts—questions, instructions, descriptions, and the like. These responses are generated by repeatedly outputting the most likely next expression given the prompt and output generated so far. ChatGPT is so good at human-style interaction that it can fool you into thinking you’re talking to a human.

But despite their awesome performance on many linguistic tasks, when it comes to reasoning, such as precise mathematical calculations, and the like, the performance of LLMs is rather poor.

Many leading researchers frame the issue in terms of a distinction that’s been popularized by Daniel Kahneman in his famous popular science book Thinking, Fast and Slow.

In the book, Kahneman describes the distinction between two kinds of reasoning activities regularly performed by human agents:

System 1 thinking, which is fast, automatic, intuitive, unconscious, associative, and the like. Examples:
- recognizing a face,
- telling if one object is taller than another,
- performing simple calculations, like 5+7,
- …
System 2 thinking, which is slow, deliberate, conscious, logical, calculating, and the like. Examples:
- counting the number of A’s in a text,
- solving a logic puzzle,
- performing complex calculations, like 432\times 441,
- …

The diagnosis of the problem with LLMS shared promoted, e.g., by Andrej Karpathy is that LLMs are really good at system 1 thinking, but are lacking in system 2 capabilities. Symbolic systems, like expert systems, instead, are really good at system 2 thinking, but have little to no system 1 capabilities. There are different ways of tackling this problem, but one promising way that’s being explored by companies like OpenAI at the moment is to create hybrid systems, which both have symbolic and subsymbolic components. Think of teaching ChaptGPT to use calculator rather than letting it try to solve a calculation “in its head”.

Another way in which logic-based methods play a role in recent research is in XAI. When a statistics-based AI system, especially an ANN- based system, makes a prediction (image classification, text prediction, etc.) it can be very hard to figure out why it made this prediction. This is because of the opaque nature of statistics-based systems and the way they are learned from data. One popular approach in XAI is to try to extract if-then rules from the underlying ANN.

Finally, it is important to note that statistics-based AI systems still typically rely on inference, just statistical, inductive inference and not the deductive inference that’s typically used in logic-based AI systems. In fact, the stage of next-word-prediction in LLMs is called “inference”: the system infers which piece of text should come next given the previous text as premise information. This prompts us to revisit Shannon’s connection between circuits and Boolean truth-functions mentioned above: can we perhaps understand ANNs in a similarly structured way through the lens of inductive logic?

The bottom-line is that even if logic-based AI is no longer “the only game in town”, you still need to learn logic and logical methods if you want to understand AI research.

Logic and AI

What is AI?

What is logic?

Logical systems

Logic and AI

Foundational

Methodological

Auxiliary

The way forward

Further readings