Probability and inductive logic

---

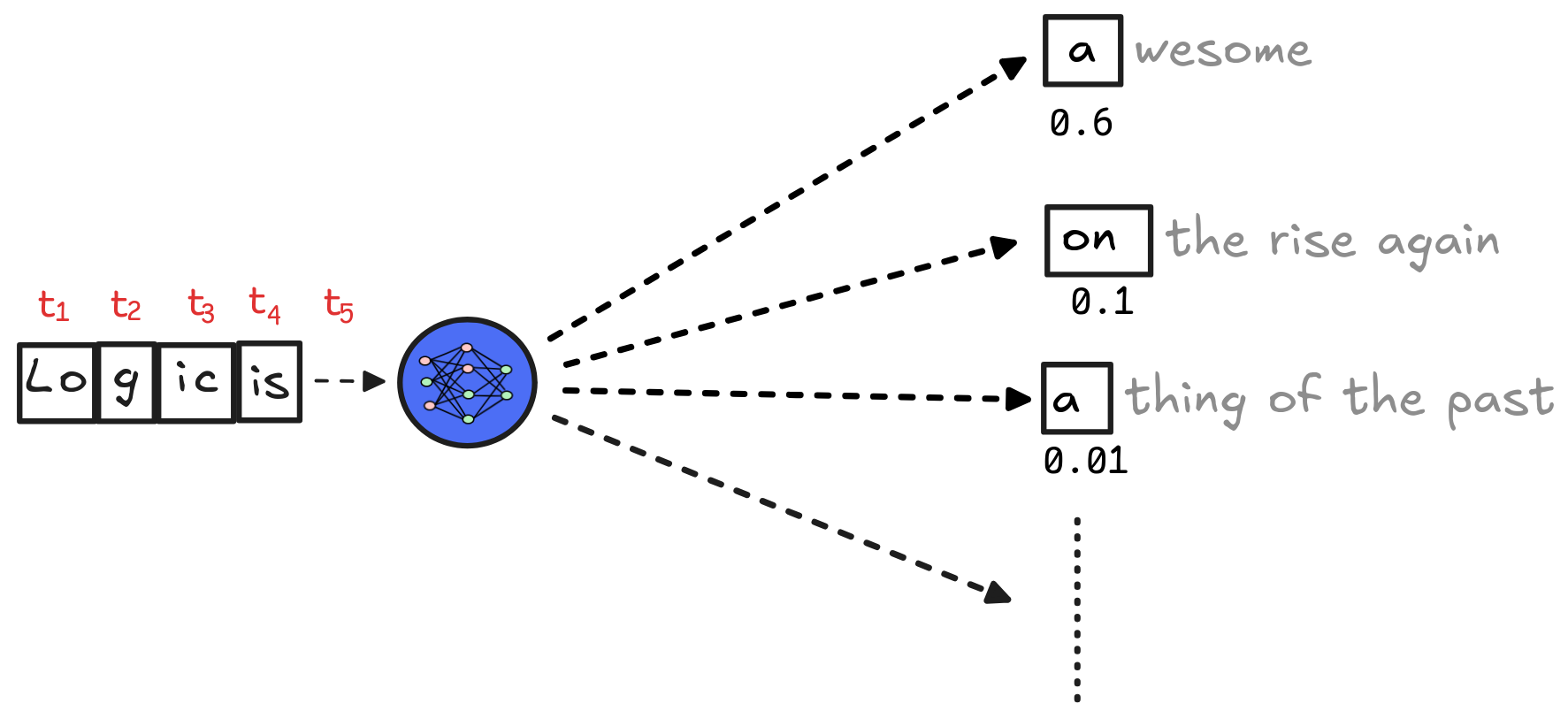Inductive inference plays a crucial role in AI technologies both on the low level and on the high level. On the low level, inductive inference is, for example, the logical foundation for large language models (LLMs), which in turn give us chatbots and other modern AI technologies. In essence, an LLM is (an approximation of) a probability distribution over tokens—small-ish sequences of characters that make up words. The idea is that we can use the conditional probability of one token given a sequence of others to predict what the next token in the sequence should be. The perhaps surprising fact is, that this “next-token prediction” allows us to develop AI agents with human-like abilities.

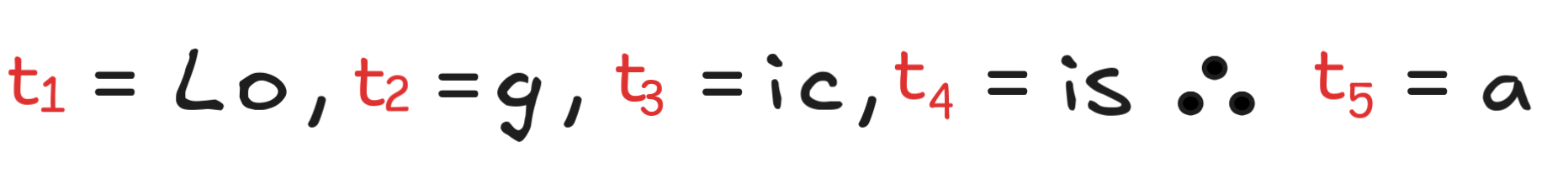LLMs, and the technologies that they are based on, are the state of the art of statistics-based AI: they are not based on hand-written if-then rules and automated deductive inference, but on statistical models of large-scale datasets, which are developed using advanced machine learning methods, such as gradient descent. But the fact that LLMs aren’t logic-based doesn’t mean that they have nothing to do with logic. In fact, next-token prediction is a form of (inductive) inference: t₁, …, tₙ are the previous tokens, therefore s is the next token. If we want to have any hope at all of understanding how LLMs work on the low level, we need to study inductive logic.

In fact, inference that involves prediction is typically inductive—we can hardly ever make predictions with certainty. In this chapter, we’ll focus on predictive inference on the higher, propositional level. As an example of an AI-technology that features inductive inference we’ll look at SPAM filters.

There are different approaches to inductive logic in AI-research. In the logic-based tradition, there are systems which aim to assimilate inductive logic to deductive logic: they work just like the sytems we know from deductive logic in terms of syntax, semantics, and proof-theory, except that their consequence relation is inductive: it allows for the premises to be true and the conclusion to be false. The result are systems of non-monotonic logic, such as autoepistemic logic and default logic, which have a solid place in logic-based AI research.

But in broader terms, probability theory is the most widely used framework for inductive logic. In this chapter, we’ll look at probability through the lens of logical theory. As you’ll see, we can develop the standard theory of finite, discrete probability distributions using the truth-tables we’re familiar with from Boolean logic. This allows us to develop the standard theory of inductive inference in the same setting as the standard theory of deductive inference—which in turn makes it possible to compare the two.

At the end of the chapter, you’ll be able to:

• explain the basic concept of a probability distribution over a propositional language,
• define probability distributions using classical truth-tables and probability weights,
• calculate conditional probabilities using Kolmogorov’s definition and Bayes formula,
• explain the relevance of probability to inductive inference and apply this in examples, such as naive Bayes filters,
• explain the logical relation between inductive and deductive inference.

Probabilities

---

Lets think back to our example of a six-sided die. When we’re rolling the die, we don’t know what the outcome will be. A process that has different possible outcomes is called random in probability theory. In our case, there are six possible outcomes: we could roll a 1, a 2, a 3, a 4, a 5, or a 6. Visually, we can represent these possible outcomes as: 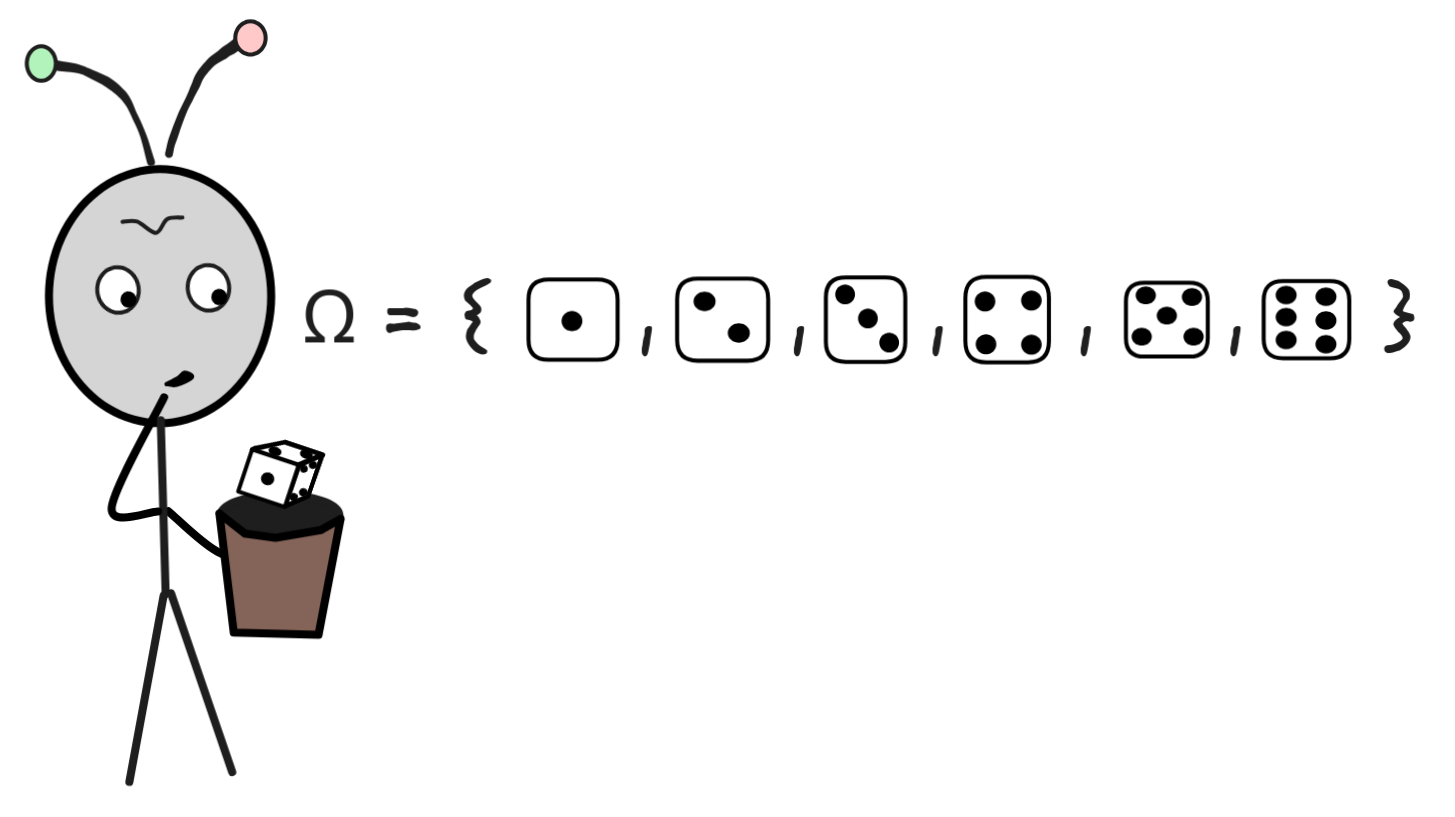In probability theory, the symbol Ω stands for the so-called sample space, from which our possible outcomes are recruited. Rolling the die is what’s called a random experiment, which is a procedure that decides the random process by settling the outcome.

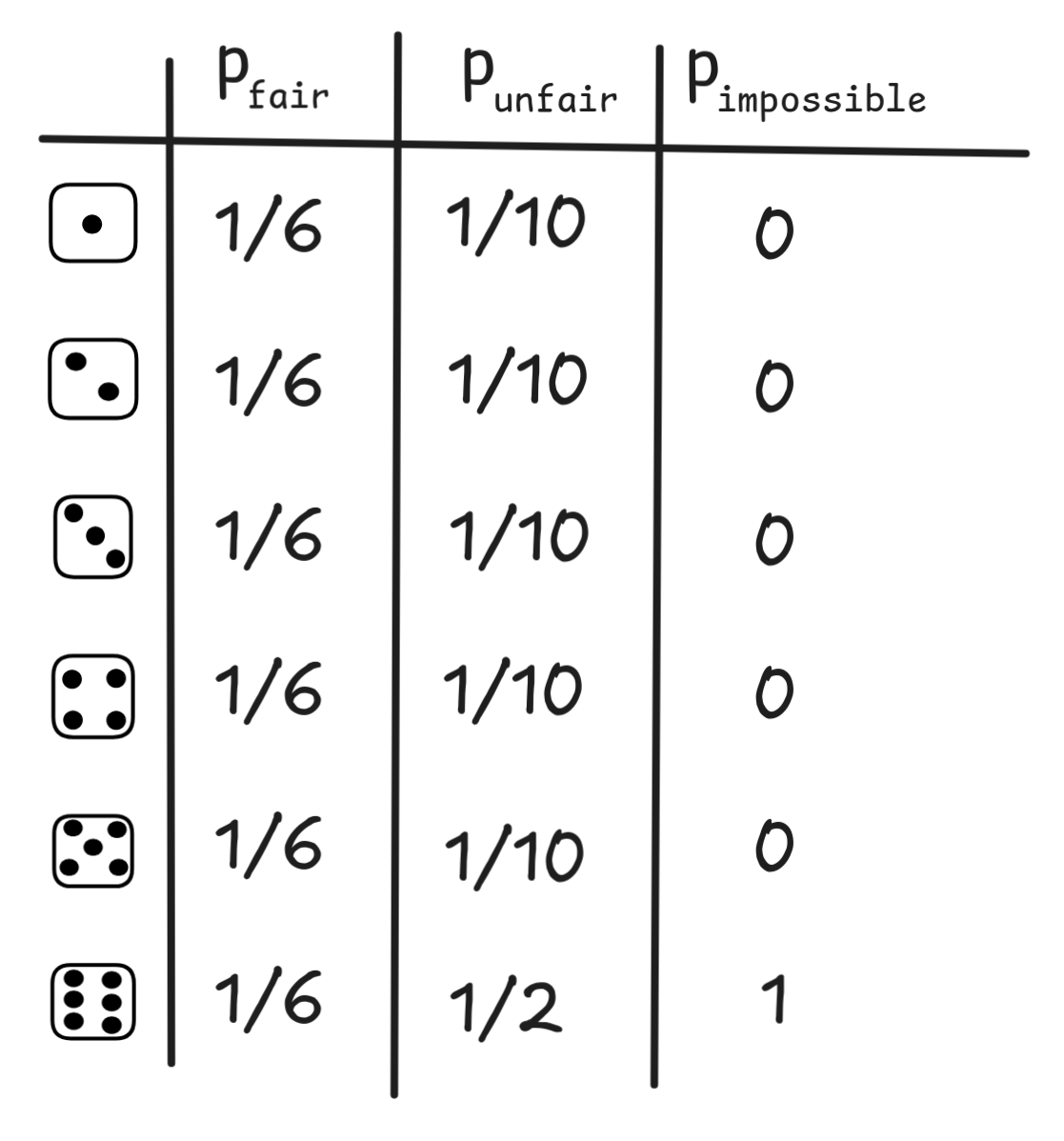
Each outcome in our experiment has a chance of occurring, but what this chance is depends on the die. On a fair die, each outcome is equally likely. On a loaded die, instead, some outcomes are more likely than others. So, there is no “intrinsic” chance that we must assign to the outcomes given our setup of rolling a 6-sided die. There are different possible ways of assigning chances, which correspond to different ways the world could be like.

Formally, we model these different probabilities using what’s called a probability mass function, which is often denoted p. This is a mathematical function that assigns a value between 0 and 1 (inclusive) to each of our outcomes to measure its chance of occurring. The value 0 means that it’s impossible for the outcome to occur, and the value 1 means that it’s absolutely certain. Intermediate values measure the chance with a higher value meaning a higher chance.

The only constraint on a probability mass function is that the sum of the values over all outcomes must be one, i.e.

This constraint captures the idea that at least one of the outcomes must obtain. And behind this way of mathematically expressing this constraint is the idea that the chance of one of sequence of mutually exclusive outcomes to occur is the sum of the chances of these outcomes. That is, what we’re saying here is that: the chance of the roll either being a 1, a 2, a 3, a 4, a 5, or a 6 is 1—it’s absolutely certain that at least one outcome will occur.

Other than that, any distribution of masses over the outcomes defines a probability. That is, all of the following are perfectly fine probability mass distributions:

Once we know the chances of the basic outcomes, we can calculate the probabilities of complex outcomes, like the die showing an even number or showing a number bigger than four. In the parlance of probability theory, these are called events. An event is a set of basic outcomes, the basic outcomes which correspond to the event. So, for example, the event that die shows an even number is:

Instead, the event that the roll is bigger than four (exclusive) is:

To calculate the probability of an event, we simply sum up the probability masses of its outcomes. So, for example,

This probability, then, will differ for each mass function. For our fair die, e.g., we get Pr({ , , }) = 1/6 + 1/6 + 1/6 = 3/6 = 1/2. But for the unfair distribution, we get Pr({ , , }) = 1/10 + 1/10 + 1/10 = 3/10. Since each outcome ω Ω corresponds to a singleton event, viz. {ω}, we can also write things like Pr( ), which technically would be Pr({ }) = p( ). More generally, the formula for the probability of an arbitrary event X Ω is:

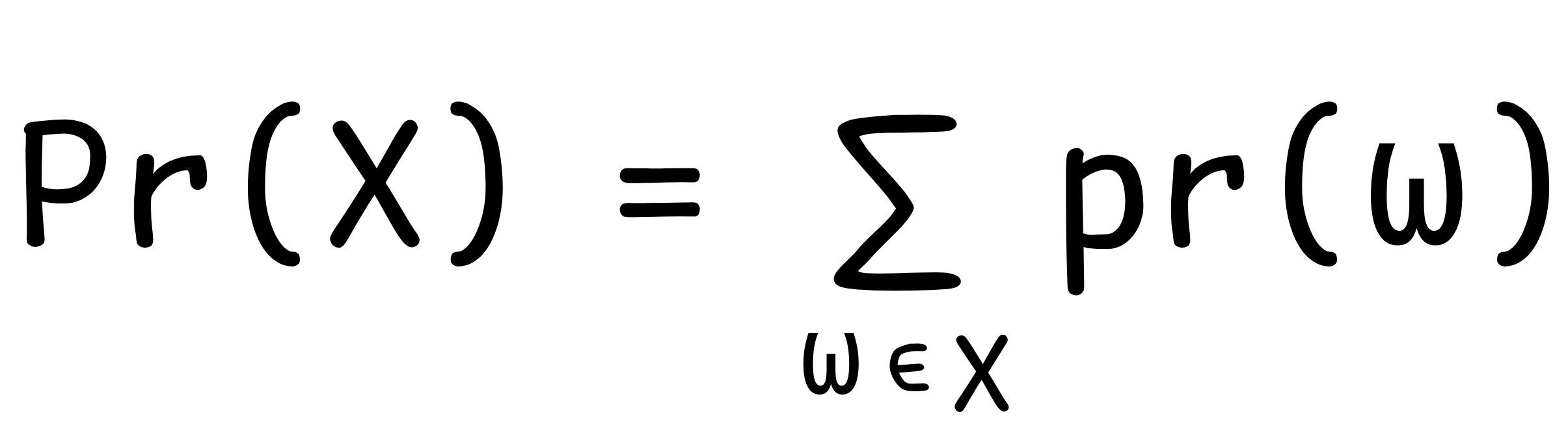
This is, in a nutshell, the standard model of (finite) discrete probabilities. Things get a bit more complicated if we want to allow for non-discrete continuous values: where the outcomes cannot be counted like 1, 2, 3, … but are things like real-valued functions with values in an interval [0, 1]. But for the purposes of basic AI-applications, discrete probability theory is more than enough.

There is a big debate on the foundations of probability theory concerning what probabilities are:

• for Bayesians probabilities are a measure of one’s degree of belief in something happening;

• for frequentists, probabilities measure how often an event would occur if we’d repeat the experiment infinitely many times;

• for objectivists probability is something “in the world”: just like there’s the mass of an object, there’s the chance of it behaving a certain way.

For our purposes, however, the interpretation of probabilities is not crucial. To explore the relation between probabilities and inductive inference in AI, we can take a naive view of probabilities as chances or likelihoods of something happening.

Note that the outcomes of a random experiment are nothing different than the reasoning scenarios we’ve discussed on logical semantics. Suppose, for example, that rather than a die roll, our random experiment is given by tomorrow’s weather with respect to sun and rain. In this setup, there are four possible outcomes:

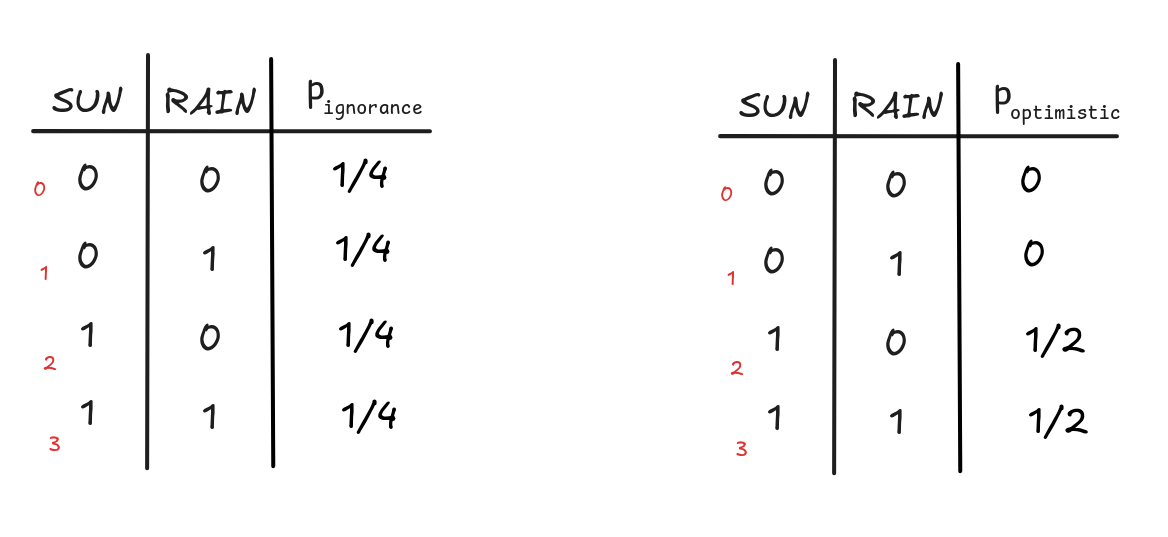
But these are just the models for the propositional language with SUN and RAIN. In fact, we can think of a probability mass function as an assignment of values between 0 and 1 to the models of this language. A convenient way of displaying them is by means of a probabilistic truth-table, which next to the truth-values, gives the probability of a given row. Here’s, for example, two probabilistic truth-tables: one table that represents a situation where we don’t know what’ll happen tomorrow, where each outcome is equally likely, and one table that represents a situation where we know that the sun will shine but it’s uncertain whether it will rain or not:

Given a probability mass function over the models of a language, we can calculate the probabilities of arbitrary formulas by calculating the probability of the proposition they express. Remember that the proposition A expressed by a formula A is simply the set of models where the formula is true:

But in probabilistic terms, such a proposition is just an event over the sample space of valuations or models. So, the rules from before tell us that:

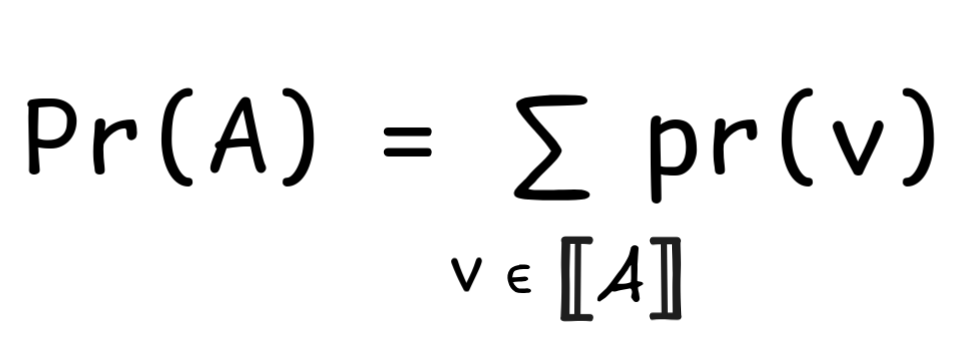
That is, to determine the probability of a formula given a probability mass function, we sum up the masses of all the valuations under which the formula is true.

Truth-tables are of great help here: if you have a probabilistic truth-table—like the ones above—you can simply calculate the values of your formula in question for each row, and then sum up the weights of the rows where the outcome is 1. Here’s how this works out for our two examples and the formula SUN RAIN: 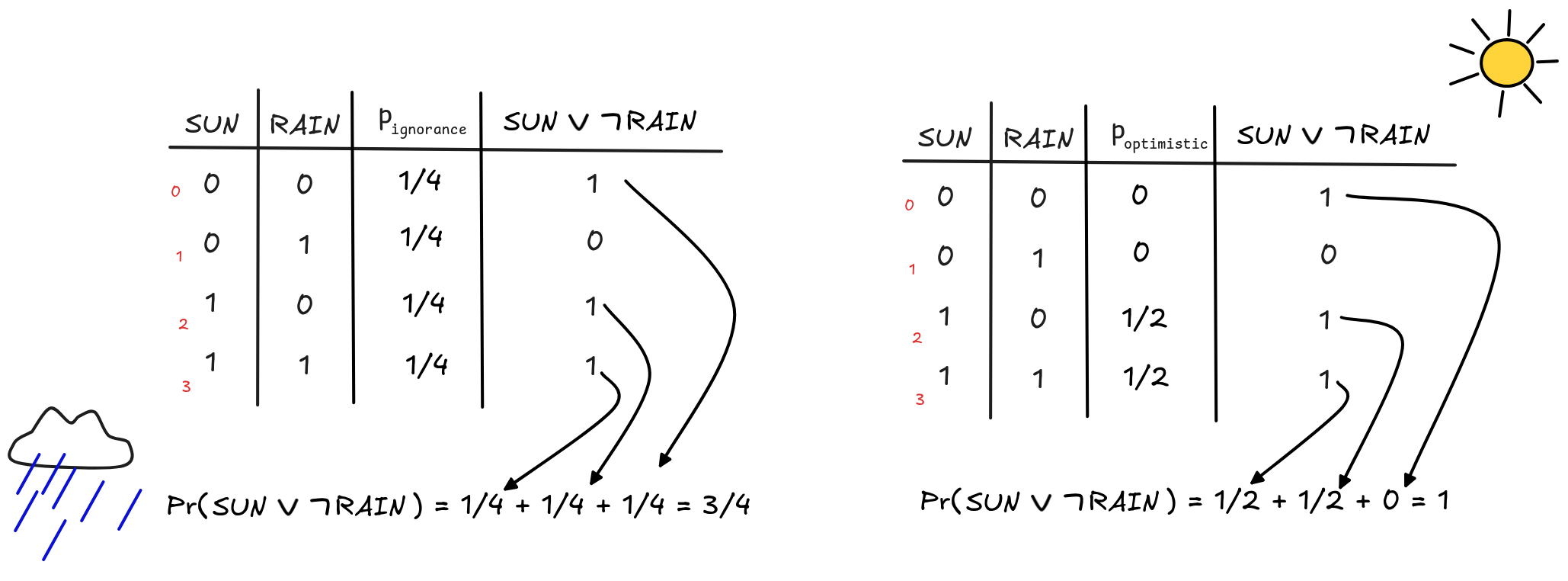In this way, given a probability mass, we can calculate the probability of each formula.

There’s a crucial difference between truth and probabilities, which is important to pay attention to. The truth-values of complex formulas are calculated recursively, which means step-by-step from the values of their parts. The probabilities of complex formulas, however, are not (in general) recursive. Take, for example, the probability of SUN RAIN under the ignorance distribution and compare it to the probabilities of SUN and RAIN:

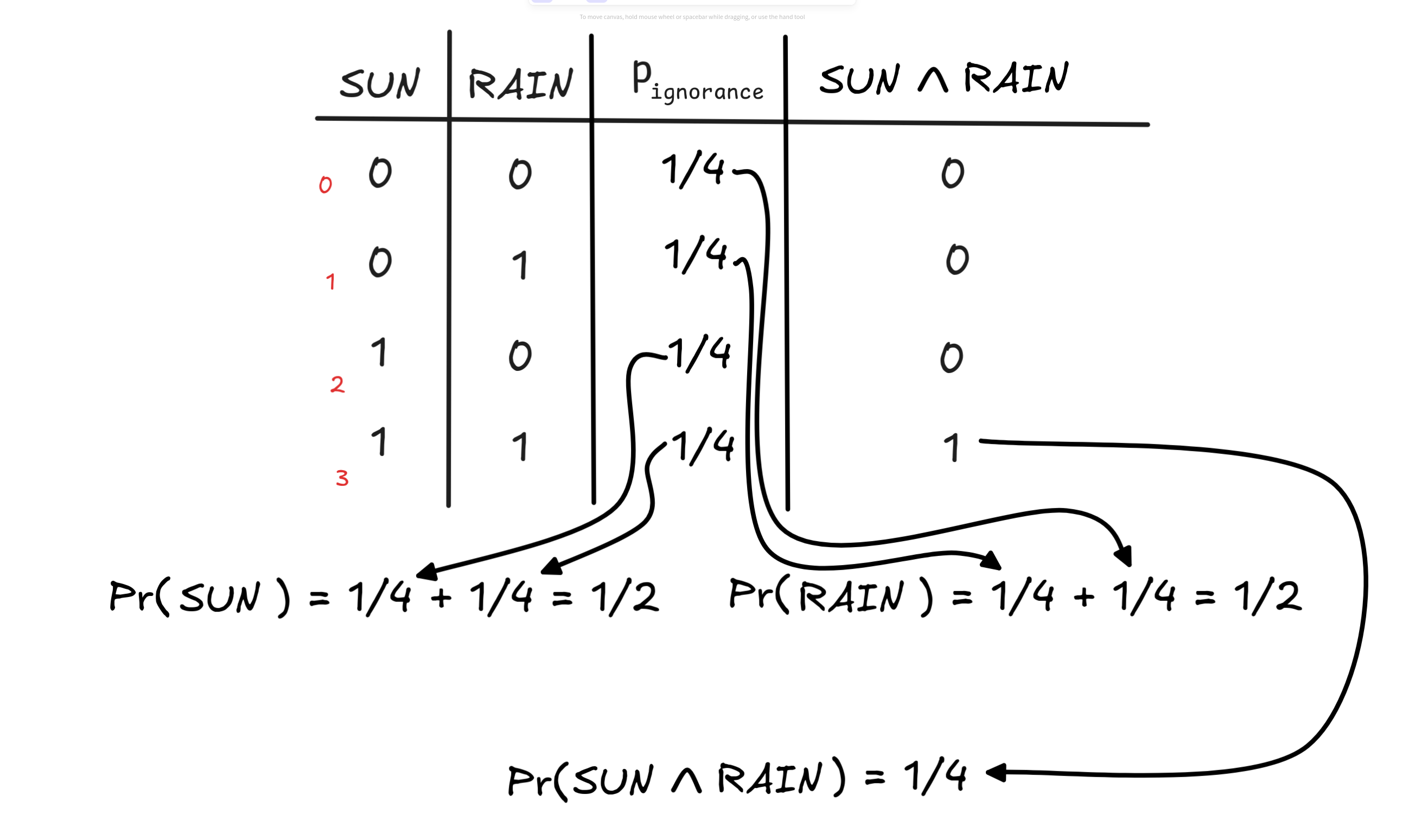
With this probability mass distribution, we have that

But this formula doesn’t apply under all distributions. Look, for example, at the following table with the distribution p*:

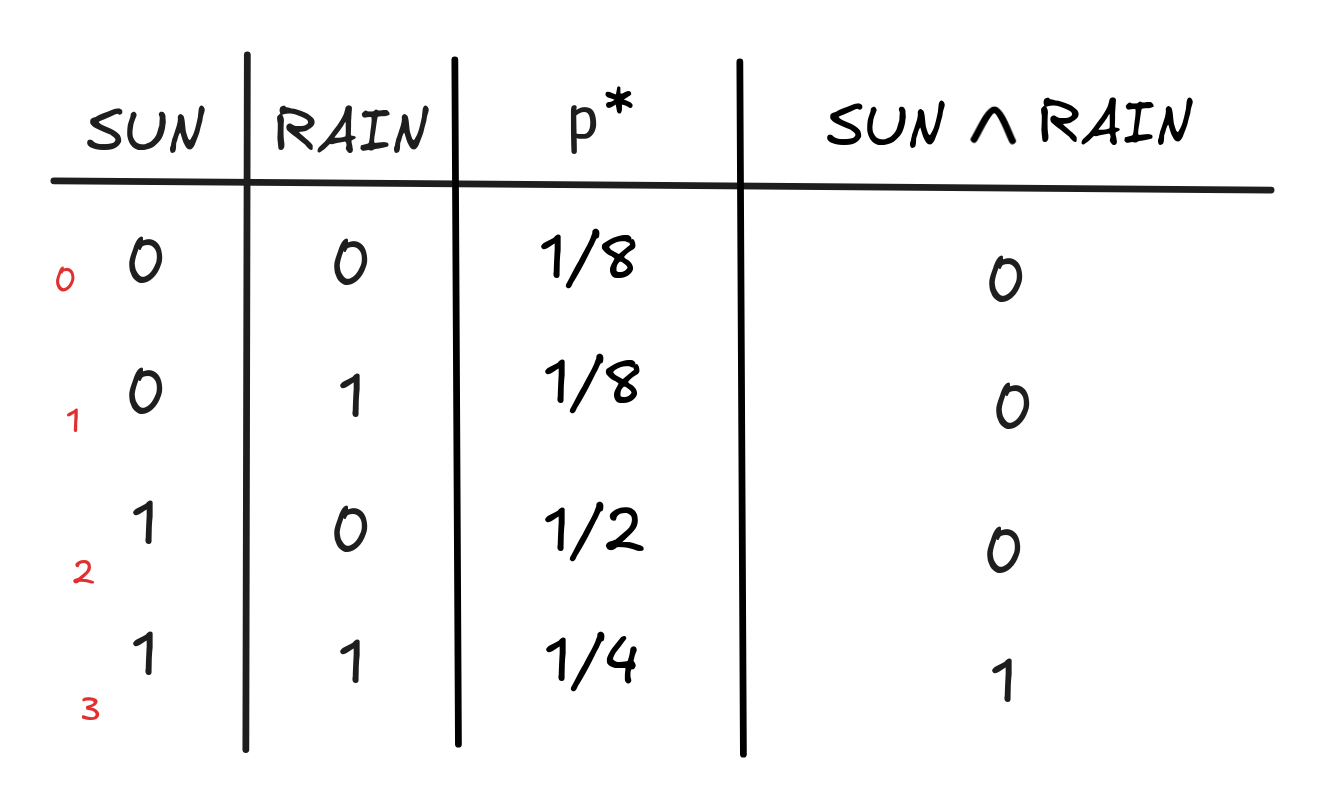
This table represents a situation where it’s more likely to be sunny than not. We have:

If we’re looking at the situations where the sun shines, it’s relatively unlikely that it will rain: the world where the sun shines and it’s not raining has probability 1/2 and the one where the sun shines and it’s raining has probability 1/4.

If instead, we look at the two situations where the sun isn’t shining, we see that it’s equally likely among those that it’s raining: both scenarios, sun and rain as well as sun and no rain, have probability 1/8. The probability that it’s raining is therefore:

But if we look at the probability of the conjunction, we get that:

And clearly, 1/4 is different from 3/4 x 3/8 = 9/32. In fact, there is no formula that allows us to calculate the probability of a conjunction purely on the basis of the probabilities of its conjuncts.

What’s going on here has to do with probabilistic independence. In the first distribution, the two facts that it’s raining and that the sun is shining are independent of each other: under the distribution, knowing that the sun is shining, this doesn’t have any influence on the probability of it raining.

To further illustrate this, we can use the concept of conditional probabilities. We’ve already seen the definition of conditional probabilities in terms of propositions when discussing valid inference:

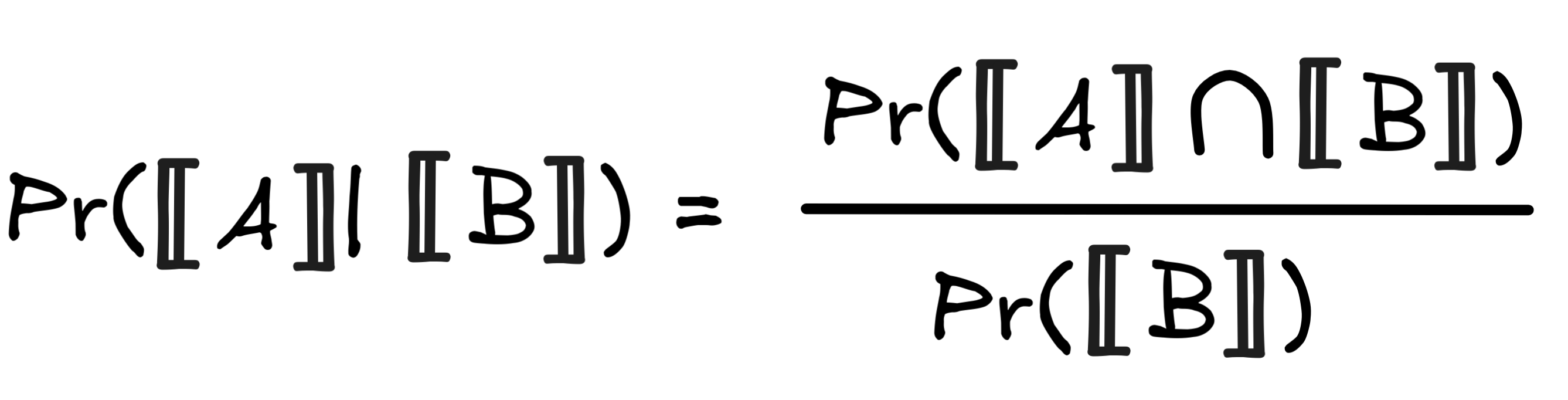
Here, the crucial condition that Pr( B ) ≠ 0 applies. But using the following identity:

we can also directly define conditional probabilities on formulas:

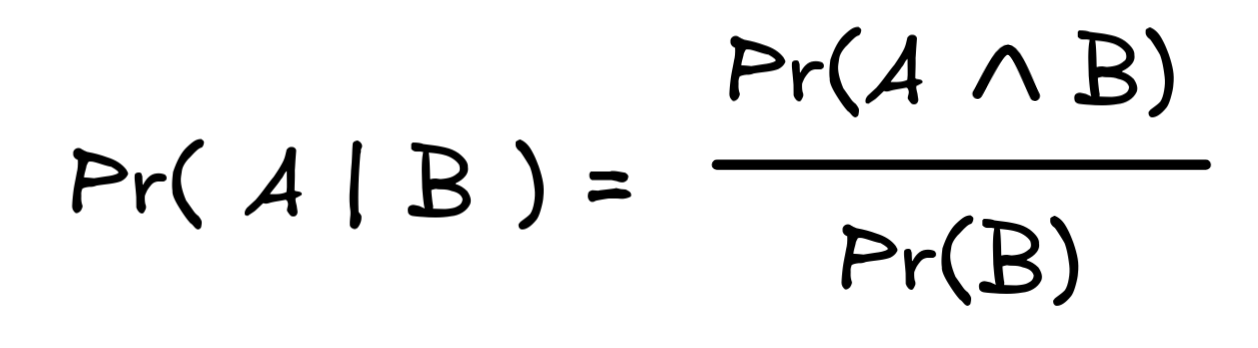
Now look at what happens in the case of our ignorance distribution, if we calculate Pr(RAIN | SUN). First, we note that:

Now, let's calculate Pr(RAIN | SUN). We get: That is, we have that In other words, the information that it's sunny doesn't tell us anything about the rain.

If we look at the distribution p*, instead, we get:

And so, we have that:

That means that under the hypothesis that it’s sunny, the probability of rain changes—in fact, it goes down (since 1/3 < 3/8).

Two formulas A and B are said to be probabilistically independent just in case if they are like SUN and RAIN in our first distribution, that is just in case

In the case where A and B are probabilistically independent, we have the

To see this, suppose that Pr(A | B) = Pr(A). By the formula for conditional probabilities, we have that Pr(A | B ) = Pr(A B)/Pr(B). So, if we multiply by Pr(B), we get Pr(A | B) x Pr(B) = Pr(A B). But since Pr(A | B) = Pr(A) by assumption, we have that Pr(A) x Pr(B) = Pr(A B).

In fact, this is a test for probabilistic independence as well: if Pr(A B) = Pr(A) x Pr(B), then Pr(A | B ) = Pr(A). This is simply because Pr(A | B) = Pr(A B)/Pr(B). So, if Pr(A B) = Pr(A) x Pr(B), we have that:

In the absence of independence, the best thing we can say about the probability of a conjunction is that:

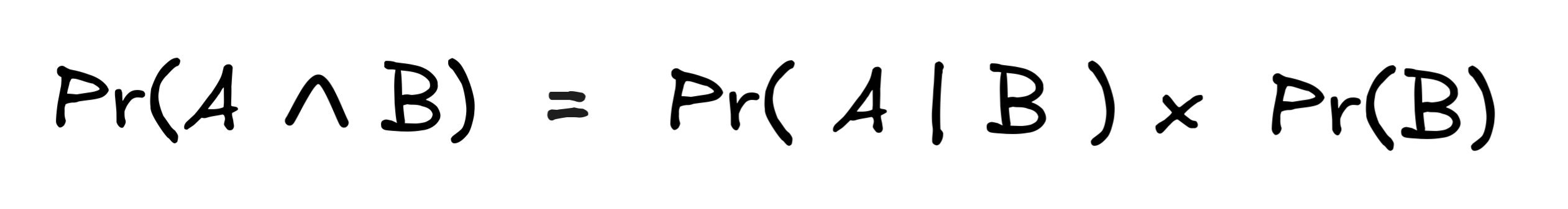
This covers conjunction. Disjunction is subject to similar considerations. Take our ignorance table and look at the disjunction SUN RAIN:

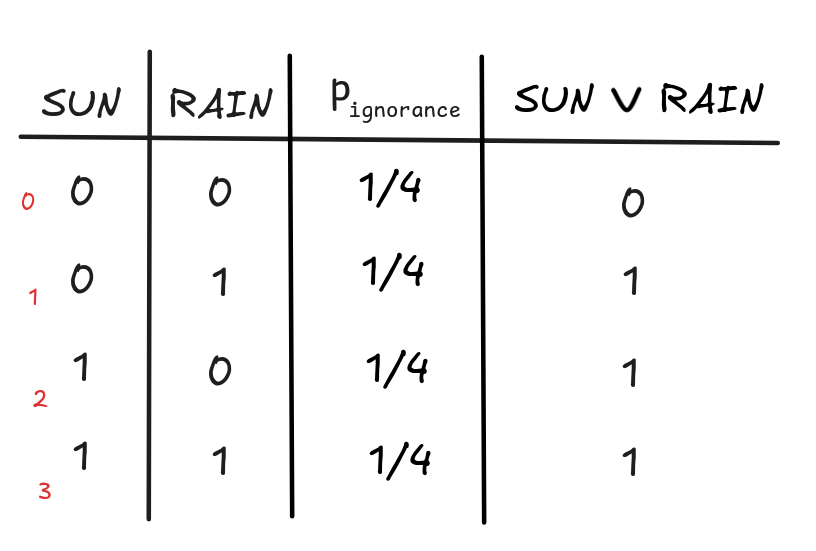
We get:

Looking at this calculation, you can note that we’re adding Pr(SUN), Pr(RAIN), and Pr(SUN RAIN) to obtain the probability of SUN RAIN.

In fact, this is the general formula for calculating disjunctive probabilities:

But that means that, in general, we cannot calculate the probability of a disjunction from the probabilities of it’s disjuncts—we also need to know the probability of their conjunction.

Only in the very special case where Pr(A B) = 0, when A and B are probabilistically incompatible, we get the recursive formula:

The only case where we have a full recursive rule is the case of negation. Under each distribution, we have

This follows from the simple fact that the rows where A is true are precisely the rows where A is not, and the masses of the rows add up to 1.

Probability Laws

---

The fact that probabilities aren’t recursive puts special emphasis on the laws of probability. Moreover, in AI research, you’re often dealing with situations where its practically intractable to go through all possible models of the premises and assign them probability masses. Instead, you’ll be estimating the relevant probabilities of the formulas directly. And when you do that, you have to make sure you’re doing this in accordance with the laws of probability.

The standard axiomatization of probability is due to Andrey Komogorov and correspondingly known as the Kolmogorov axioms. We can formula these axioms in logical terms and directly in terms of events. First, the logical axiomatization. It states that for each assignment of probabilities Pr to formulas in a language, the following laws apply:

1. Pr(A) ≥ 0, for all formulas A.
2. Pr(A) = 1, if A is a tautology, that is: A.
3. Pr(A B) = Pr(A) + Pr(B), given that A and B are logically incompatible, that is: (A B).

As you can see, these axioms are rather minimal. But it turns out that they are sound and complete with respect to the probabilities we’ve defined in terms of probability mass distributions over valuations. That is, every law about probabilities that holds for all probabilities Pr defined in terms of probability mass distributions is derivable form these laws, and everything that’s derivable holds for all distributions.

For example, here’s how we derive the law of negation:

• Pr(A A) = 1, by axiom 1. since A A.
• Pr(A A) = Pr(A) + Pr( A) by axiom 3. since (A A).
• It follows that 1 = Pr(A) + Pr( A).
• But that gives us: Pr( A) = 1 - Pr(A)

From this it immediately follows that Pr(A) 1 for all A, since Pr(A) = 1

• Pr( A).

Or, we can derive that if A B, then Pr(A) Pr(B):

• Pr(A B) = Pr(A) + Pr( B), by axiom 3., since from the assumption that A B it follows that A B—that is if A and B is unsatisfiable.
• Since Pr( B) = 1 - Pr(B), we have Pr(A B) = Pr(A) + (1 - Pr(B)).
• So, we get that Pr(B) = Pr(A) + (1 - Pr(A B)).
• But we know that Pr(A B) 1, so 1 - Pr(A B) is positive and so Pr(B) = Pr(A) + x, for some positive x.
• In other words, Pr(A) Pr(B).

We can give these axioms completely equivalently directly in terms

1. 0 Pr(X), for all events X Ω
2. Pr(Ω) = 1
3. Pr(X Y) = Pr(X) + Pr(Y), given that X Y = ∅.

This axiomatization says precisely the same thing as the previous one once we realize that A = Ω means that A is a logical truth and

Naive Bayes Classifiers

---

To see how AI-technologies use probabilities for inductive inferences, let’s look at an example: spam filtering with naive Bayes classifiers.

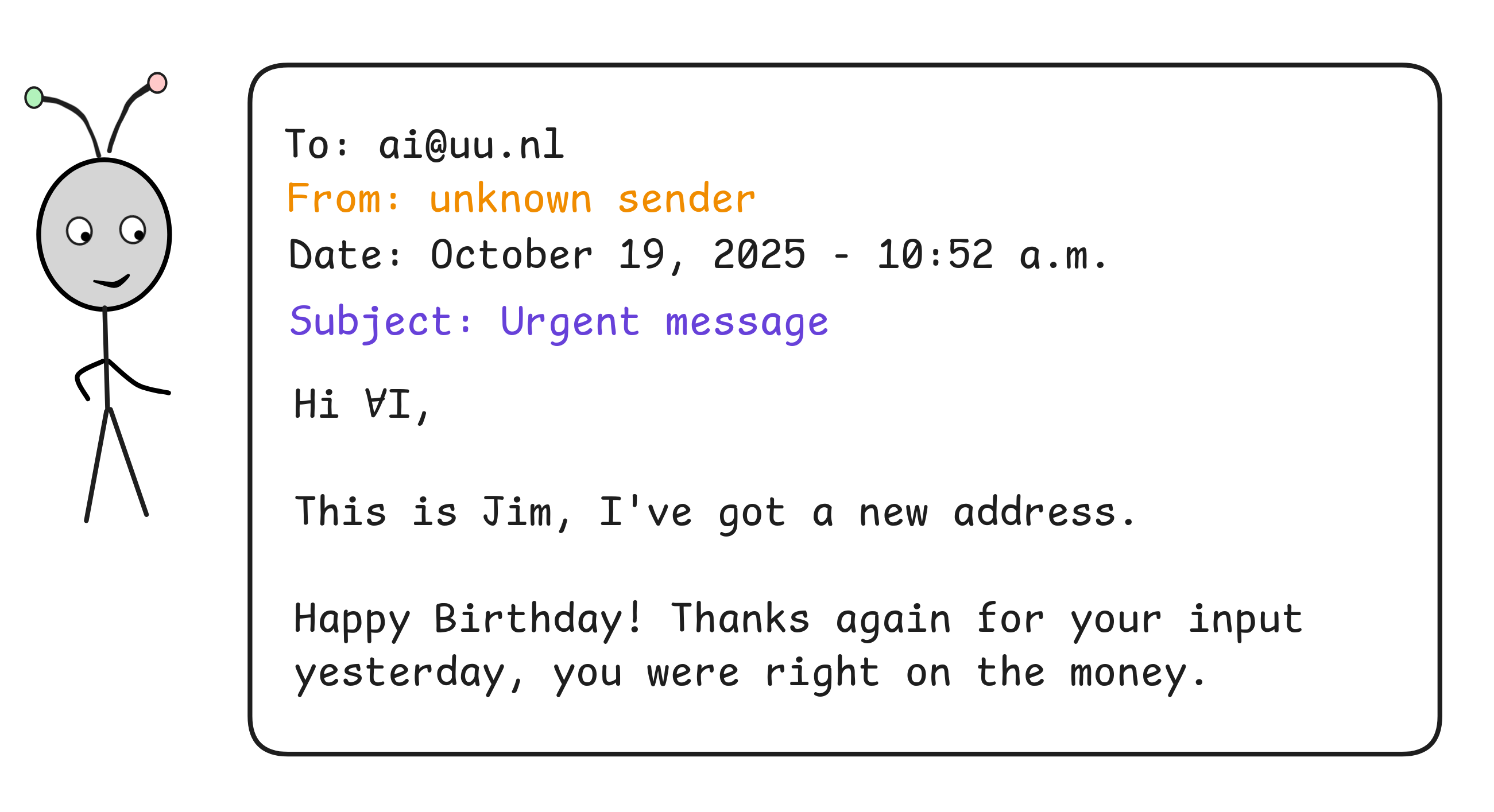
For our example, let’s suppose that IA  receives an email:

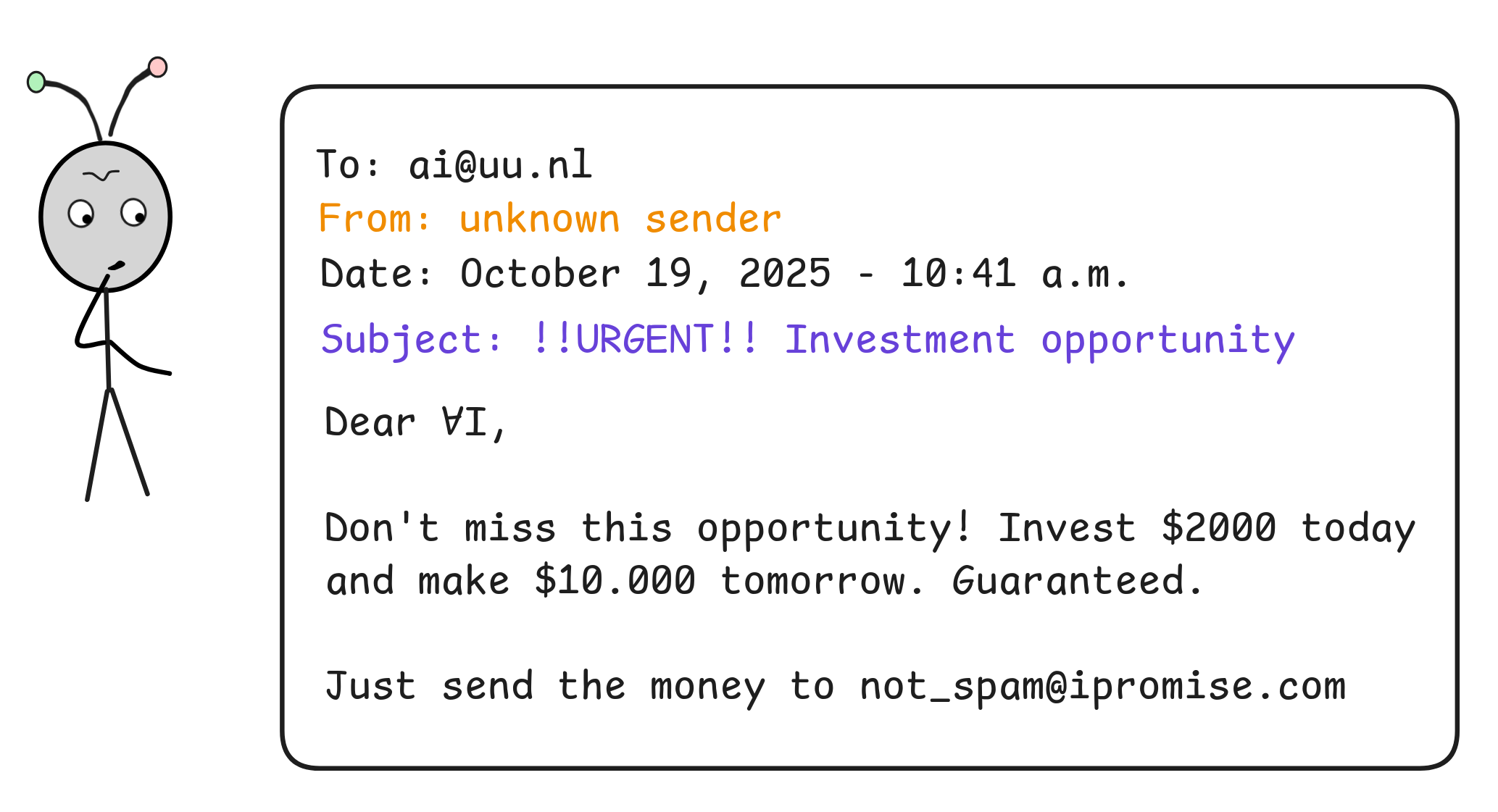
How can IA  tell that this is a SPAM email?

Since we’re in a logic course, you might think that we’d try to develop an expert system for this task. We devise a propositional language with atoms like

In this language, we can formula conditional rules like:

• (SubjectUrgent MoneyTalk) SPAM
• (ExlamationMarks SubjectUrgent) SPAM
• …

Then we could run a filter through each email and check whether the propositions UnknownSender, SubjectUrgent, ExclamationMarks, MoneyTalk are true and use the KB to see if we can derive SPAM using methods like forward chaining or backward chaining or resolution.

But the problem with this approach is that none of these indicators are 100% reliable. We can have an email that satisfies all of them but is perfectly harmless:

That is, using deductive inference will lead to a lot of false positives. In fact, the conditions that we’ve mentioned aren’t logically sufficient for an email being SPAM, they are fallible evidence for it.

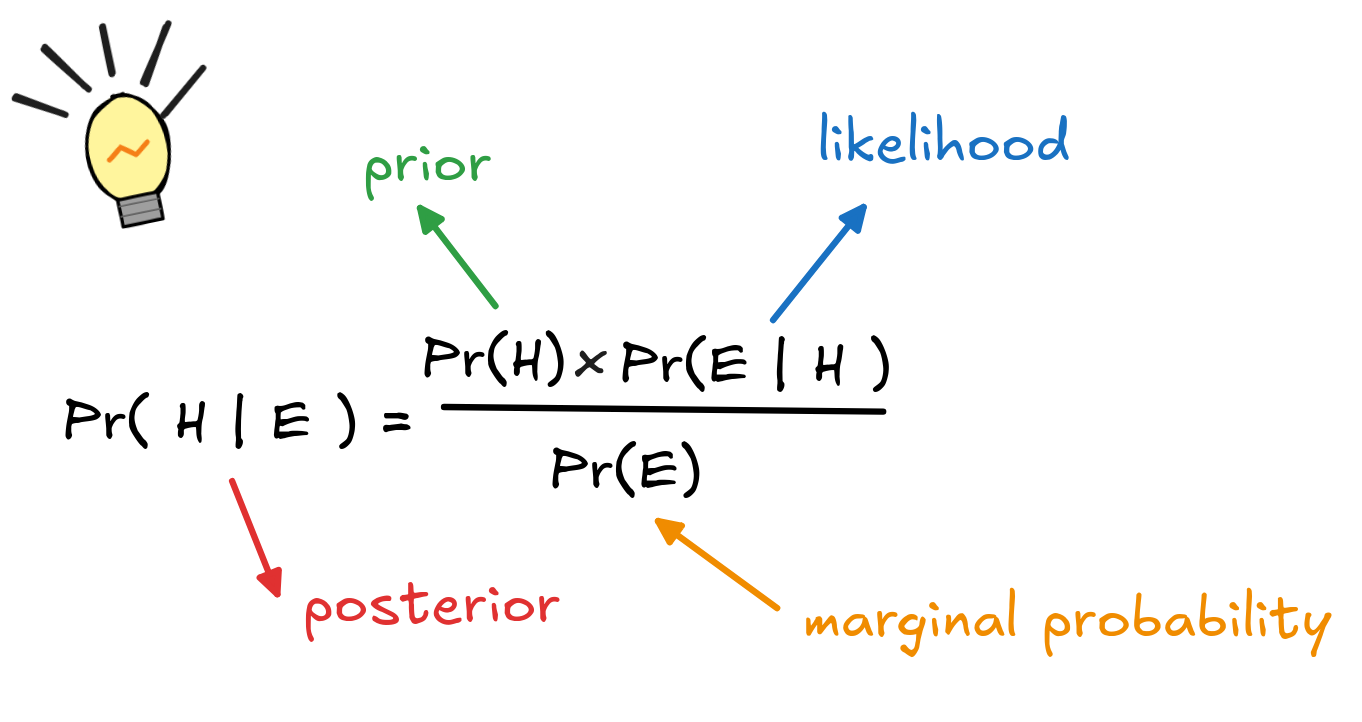
A powerful approach to inductive inference uses probabilities and Bayes' rule. The basic idea is that we can say that a piece of propositional evidence, E, confirms a hypothesis, H, just in case:

That is, the evidence confirms the hypothesis just in case the probability of the hypothesis goes up if we assume the evidence. In other words, evidence is a form of inductive inference.

So, what we’re looking for is Pr(SPAM | [MARKERS]), where [MARKERS] is a combination of things like UnknownSender, SubjectUrgent, ExclamationMarks, MoneyTalk. That is see whether the present markers are evidence for the mail being SPAM, we need to calculate Pr(SPAM | [MARKERS]) as well as Pr(SPAM).

Bayes rule is, in essence, a convenient way of calculating Pr(SPAM | [MARKERS]):

This calculation is derived by simply substituting P(H E) with Pr(H) x Pr(E | H) from the general rule for conjunction. The terms in the equation have suggestive names:

• Pr(H | E) is known as the posterior probability of the hypothesis given the evidence.

• Pr(H) is called the prior probability of the hypothesis, independent of the evidence.

• Pr(E | H) is known as the likelihood of the evidence given the hypothesis.

• Pr(E) is known as the marginal likelihood of the evidence.

Plugging in SPAM and [MARKERS], we obtain:

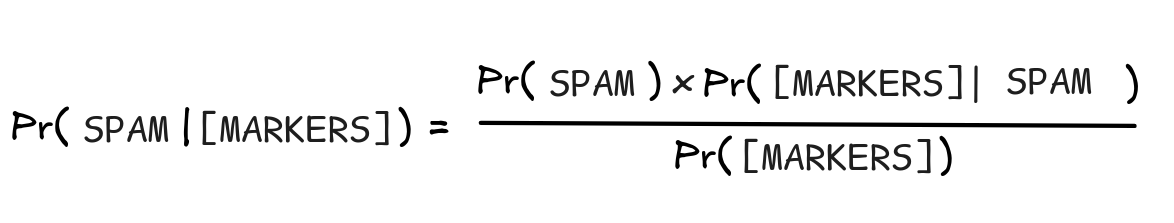
This is progress: the prior probability, Pr(SPAM), we can estimate using the frequency of SPAM. For this example, let’s estimate it optimistically as 20%. In probabilistic terms:

For individual markers, like UnknownSender, SubjectUrgent, ExclamationMarks, MoneyTalk, we have to estimate the marginal likelihood Pr([Markers]) and likelihood Pr([Markers] | SPAM). In practice, this happens on the basis of a frequency analysis of datasets of emails, especially the ones you have received. For each marker, we can easily check how often it occurs in an email: how many emails are from unknown sender, how many emails have “urgent” in the subject line, and so on. Dividing these numbers by the total number of emails gives us a decent estimate of their respective probabilities. We might, for example, find:

The same procedure, we can use to estimate the likelihoods for the markers given in SPAM messages. What’s the frequency of SPAM emails with an unknown sender, SPAM emails with urgent subject line, etc. For example, we might find:

We can plug this data into Bayes rule and obtain estimates of how likely it is that an email is SPAM given that it comes from an unknown sender:

Since

receiving an email from an unknown sender is evidence of it being SPAM—but not very strong evidence.

What does this mean? Well, for one, the probability of the email being SPAM only went up by 0.06. This is the so-called increase of firmness measure

In our case, the increase of firmness is not very strong.

But note that the probability of the email being SPAM went up from 0.2 to 0.26, which is a 30% increase. This is known as the the ratio measure:

There are many more such confirmation measures. In fact, in industry implementations of naive Bayesian classifiers the co-called log-likelihood ratio is commonly used, but we won’t go into the more involved mathematical details here.

Different measures have different advantages: for example, the increase of firmness gives an intuitively clear and robust measure of strength of evidence, but it doesn’t work very well with evidence and hypotheses close to 0 or 1. The ration measure, instead also works well close to extreme values, but it is not normed—in particular it’s value can get arbitrarily high making comparisons difficult.

But regardless of different measures of how much weight the evidence carries, there’s another fundamental question we’ve got to address: if the posterior probability is “only” 0.26, it’s still more likely that this isn’t SPAM than that it is. What we need to do is to set a threshold for classifying email as SPAM. A natural minimum is to say that Pr(H | E) should at least be 0.5. But if false positives are particularly bad—when classifying email as SPAM that isn’t risks important messages to be missed—we should set the bar high. Perhaps we want to have 0.75? 0.8? It ultimately depends on the stakes of the situation, but let’s try to reach 0.5 in our SPAM filter.

To achieve this, we need to combine different markers. What we want to do is to combine different SPAM-markers. In fact, our example mail had them all. So, we want to calculate:

But now we have a new kind of probability to estimate: the conjunctive probabilities of the markers. In fact, if we want our classifier to not only work in this case, but also when one or more of the markers are absent. But since conjunctive probabilities are not recursively calculable from their conjunctions’ probabilities, this leads to a problem of combinatorial explosion In our example, we only have 4 markers, but that’s already quite a large number of conjunctions to estimate: all 4 markers by themselves, their 6 binary conjunctions (up to re-ordering), their 3 ternary conjunctions, and the conjunction of all 4 makes 14 conjunctions we need to estimate. This quickly becomes intractable.

This is where the “naive” in naive Bayes classifiers comes in. The defining assumption is that the different markers are probabilistically independent of each other, both given SPAM and not given SPAM. That is, we can calculate:

And similarly,

This, then is the naive Bayes assumption: that the different markers are conditionally independent. It is naive because it is clearly true in strict terms: whether urgent and exclamation points occur is not independent of each other. But it turns out that this gives us pretty good classifications in practice. It gives us for our email:

A pretty clear verdict, which surpasses any reasonable threshold: we’ve got a strong inductive inference that this is spam, given the observed features.

But it also allows us to quickly estimate the SPAM likelihood of other emails. For example, if the exclamation marks are absent, the formula would still give a 0.8 probability of SPAM given that the other features are still present. But if money talk is eliminated, the probability drops down to 0.46. Fine-tuning these values, checking them against real cases and learning from data is the topic of ongoing machine learning research.

Inductive logic

---

SPAM-classification is a case of material inductive inference: what counts as a good inductive inference depends on the concrete (conditional) probabilities of the premises and conclusion. Logically valid inductive inference is inductive inference that purely depends on their logical form. We can cash this out as probability raising under all probabilities:

Inductive logic is concerned with the study of inductively valid inference patterns. Today, this is mainly done as statistics and probability theory, whose study goes beyond the scope of this course. But we can get a rough idea of some core ideas by returning to one of our first examples of inductive inference: enumerative induction.

Take our inference about the marbles:

If we formalize this inference with a sufficient number of observations, we’ll look at something like:

To assess the logically validity of this inference, we need to think about the conditional probability independently of any concrete probability distribution:

For this purpose, we can make use of probabilistic theorems like the following:

Theorem: If C P₁ P₂… (the conclusion deductively implies the premises), Pr(P₁ P₂) ≠ 1 (the premises aren’t tautologies), and Pr(C) ≠ 0 (the conclusion is not impossible), then Pr(C | P₁ P₂…) > Pr(C).

To see that this must be true, we need observe the logical fact that:

Using this, we can calculate:

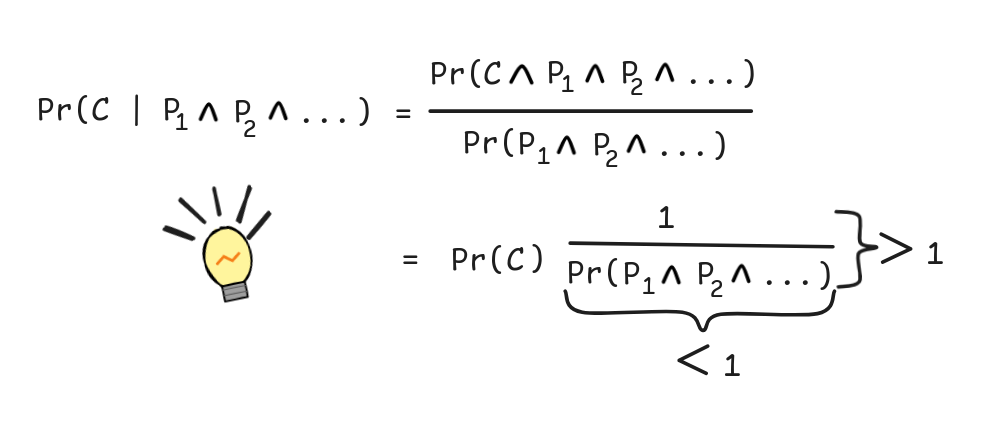
That is, since Pr(P₁ P₂ …) < 1, we know that 1/Pr(P₁ P₂ …) > 1 and so Pr(C | P₁ P₂ …) is more than one times Pr(C)—in other words, Pr(C | P₁ P₂ …) is strictly bigger than Pr(C).

This establishes that enumerative induction is at least weakly inductively valid: the premises will always raise the likelihood of the conclusion.

The strength of the inference depends on the probability of P₁ P₂ …—the less likely the premises the bigger the factor in the above equation and, correspondingly, the stronger the inference. This justifies the condition that we need to sample our premises well—it should be unlikely that they are jointly true. We can achieve this by finding many independent instances and calculate Pr(P₁ P₂ …) = Pr(P₁) × Pr(P₂) × …, which will eventually bring us below any desired threshold. Or we

Inductive reasoning is the ultimate foundation for most machine learning techniques, but also for simple algorithms like “People who liked this show also liked …"-style recommendation on streaming platforms, which makes inductive logic a fundamental tool in an AI-researchers toolbox.